Find sum of N-th group of Natural Numbers
Last Updated :
11 Aug, 2022
Given a series of natural numbers divided into groups as: (1, 2), (3, 4, 5, 6), (7, 8, 9, 10, 11, 12), (13, 14, 15, 16, 17, 18, 19, 20)….. and so on. Given a number N, the task is to find the sum of the numbers in the Nth group.
Examples:
Input : N = 3
Output : 57
Numbers in 3rd group are:
7, 8, 9, 10, 11, 12
Input : N = 10
Output : 2010
The first group has 2 terms,
the second group has 4 terms,
.
.
.
the nth group has 2n terms.
Now,
The last term of the first group is 2 = 1 × (1 + 1)
The last term of the second group is 6 = 2 × (2 + 1)
The last term of the third group is 12 = 3 × (3 + 1)
The last term of the fourth group is 20 = 4 × (4 + 1)
.
.
.
The last term of the nth group = n(n + 1).
Therefore, the sum of the numbers in the nth group is:
= sum of all the numbers upto nth group – sum of all the numbers upto (n – 1)th group
= [1 + 2 +……..+ n(n + 1)] – [1 + 2 +……..+ (n – 1 )((n – 1) + 1)]
= ![Rendered by QuickLaTeX.com \frac{n(n+1)[n(n+1)+1]}{2} - \frac {n(n-1)[n(n-1)+1]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-89692010b74eeedf1040c922a26cf372_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[(n+1)(n(n+1)+1)-(n-1)(n(n-1)+1)]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d4d3f5f2cdf907704ac1373ef39d29d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[n[(n+1)^{2} - (n-1)^{2}]+2]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-190f8b4ed3c1c0b2ebf2df8d67936cfa_l3.png)
= 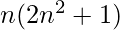
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int nth_group(int n){
return n * (2 * pow(n, 2) + 1);
}
int main()
{
int N = 5;
cout<<nth_group(N);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int nth_group(int n)
{
return n * (2 * (int)Math.pow(n, 2) + 1);
}
public static void main(String arr[])
{
int N = 5;
System.out.println(nth_group(N));
}
}
|
Python3
def nth_group(n):
return n * (2 * pow(n, 2) + 1)
N = 5
print(nth_group(N))
|
C#
using System;
class gfg
{
public static double nth_group(int n)
{
return n * (2 * Math.Pow(n, 2) + 1);
}
public static int Main()
{
int N = 5;
Console.WriteLine(nth_group(N));
return 0;
}
}
|
PHP
<?php
function nth_group($n)
{
return $n * (2 * pow($n, 2) + 1);
}
$N = 5;
echo nth_group($N);
?>
|
Javascript
<script>
function nth_group(n)
{
return n * (2 * Math.pow(n, 2) + 1);
}
let N = 5;
document.write(nth_group(N));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...