Find sum of N terms of series 1, (1+4) , (1+4+4^2), (1+4+4^2+4^3), …..
Last Updated :
20 Aug, 2022
Given a positive integer, N. Find the sum of the first N term of the series-
1, (1+4), (1+4+42), (1+4+42+43), …., till N terms
Examples:
Input: N = 3
Output: 27
Input: N = 5
Output: 453
Approach:
1st term = 1
2nd term = (1 + 4)
3rd term = (1 + 4 + 4 ^ 2)
4th term = (1 + 4 + 4 ^ 2 + 4 ^ 3)
.
.
Nth term = (1 + 4 + 4 ^ 2+….+ 4 ^ (N – 2) + 4 ^(N – 1))
The sequence is formed by using the following pattern. For any value N-
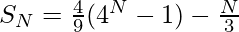
Derivation:
The following series of steps can be used to derive the formula to find the sum of N terms-
The series
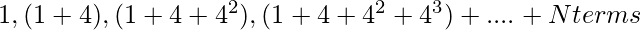
can be decomposed as-
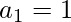
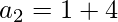
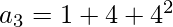
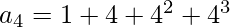
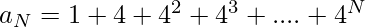 -(1)
-(1)
The equation (1) is in G.P. with
First term a = 1
Common ration r = 4
The sum of N terms in G.P. for r>1 is
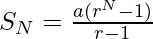
Substituting the values of a and r in the above equation, we get-
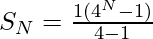
Thus, the term
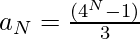
The sum of the series 1, (1+4), (1+4+4^{2}), (1+4+4^{2}+4^{3})+….+N terms can be represented as-
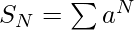
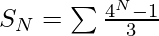
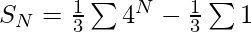
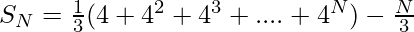 -(2)
-(2)
The equation-

is in G.P. with
First term a = 4
Common ratio r = 4
Applying the formula of sum of G.P.-
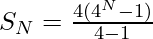 -(3)
-(3)
Substituting equation (3) in equation (2), we get-

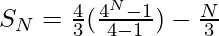
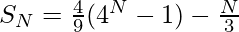
Illustration:
Input: N = 3
Output: 11
Explanation:
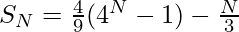
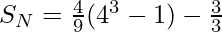
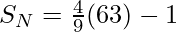
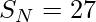
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int calcSum(int n)
{
int a = pow(4, n);
return (4 * (a - 1) - 3 * n) / 9;
}
int main()
{
int N = 3;
cout << calcSum(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int calcSum(int n)
{
int a = (int)Math.pow(4, n);
return (4 * (a - 1) - 3 * n) / 9;
}
public static void main(String[] args)
{
int N = 3;
System.out.print(calcSum(N));
}
}
|
Python3
def calcSum(n):
a = pow(4, n)
return (4 * (a - 1) - 3 * n) / 9
if __name__ == "__main__":
N = 3
print(calcSum(N))
|
C#
using System;
class GFG{
static int calcSum(int n)
{
int a = (int)Math.Pow(4, n);
return (4 * (a - 1) - 3 * n) / 9;
}
public static void Main()
{
int N = 3;
Console.Write(calcSum(N));
}
}
|
Javascript
<script>
function calcSum(n)
{
let a = Math.pow(4, n)
return (4 * (a - 1) - 3 * n) / 9
}
let N = 3
document.write(calcSum(N))
</script>
|
Time Complexity: O(log4n) because using inbuilt pow function
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...