Find sum of all odd perfect squares in the range [L, R]
Last Updated :
10 Dec, 2021
Given two integers L and R. The task is to find the sum of all the odd numbers which are perfect square in the range [L, R].
Examples:
Input: L = 1, R = 9
Output: 10
Explanation: The odd Numbers in the range are 1, 3, 5, 7, 9 and only 1, 9 are perfect squares of 1, 3. So, 1 + 9 = 10.
Input: L = 50, R = 10,000
Output: 166566
Naive Approach: The basic idea to solve this problem is to traverse the numbers in the range L to R, and for each odd number, check whether it is a perfect square as well.
Time Complexity: O(R-L)
Auxiliary Space: O(1)
Efficient Approach: The approach of the solution is based on the mathematical concept of sequence. The idea is to use sum of square of first N odd numbers.
Squares of first n odd natural numbers = 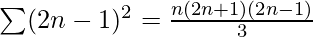
Follow the steps below to solve the problem.:
- Check count of perfect squares between 1 and the perfect squared odd number just greater or equal to L.
- Check count of odd perfect squares in range [1, L).
- Calculate sum (sum1) of odd perfect squares in range [1, L).
- Check count of perfect squares in range [1, R].
- Check count of odd perfect squares in range [1, R].
- Calculate sum (sum2) of odd perfect squares in range [1, R].
- Subtract sum1 from sum2 to get the sum of odd numbers which are perfect squares in range [L, R].
Below is the implementation of the above approach:
C++
#include <cmath>
#include <iostream>
using namespace std;
int findSum(int L, int R)
{
if (L < 0 || R < 0 || L > R)
return -1;
int l, r, n1, n2, s1, s2;
l = ceil(sqrt(L));
if (!(l & 1))
l++;
r = floor(sqrt(R));
if (!(r & 1))
r--;
n1 = floor((float)l / 2);
n2 = ceil((float)r / 2);
s1 = n1 * ((4 * n1 * n1) - 1) / 3;
s2 = n2 * ((4 * n2 * n2) - 1) / 3;
return s2 - s1;
}
int main()
{
int L = 1;
int R = 9;
cout << findSum(L, R);
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static int findSum(int L, int R)
{
if (L < 0 || R < 0 || L > R)
return -1;
int l, r, n1, n2, s1, s2;
l = (int)Math.ceil(Math.sqrt(L));
if ((l & 1) == 0)
l++;
r = (int)Math.floor(Math.sqrt(R));
if ((r & 1) == 0)
r--;
n1 = (int)Math.floor((float)l / 2);
n2 = (int)Math.ceil((float)r / 2);
s1 = n1 * ((4 * n1 * n1) - 1) / 3;
s2 = n2 * ((4 * n2 * n2) - 1) / 3;
return s2 - s1;
}
public static void main(String args[])
{
int L = 1;
int R = 9;
System.out.println(findSum(L, R));
}
}
|
Python3
import math
def findSum(L, R):
if (L < 0 or R < 0 or L > R):
return -1
l = math.ceil(math.sqrt(L))
if (not (l & 1)):
l += 1
r = math.floor(math.sqrt(R))
if (not (r & 1)):
r -= 1
n1 = math.floor(l / 2)
n2 = math.ceil(r / 2)
s1 = int(n1 * ((4 * n1 * n1) - 1) / 3)
s2 = int(n2 * ((4 * n2 * n2) - 1) / 3)
return s2 - s1
if __name__ == "__main__":
L = 1
R = 9
print(findSum(L, R))
|
C#
using System;
class GFG
{
static int findSum(int L, int R)
{
if (L < 0 || R < 0 || L > R)
return -1;
int l, r, n1, n2, s1, s2;
l = (int)Math.Ceiling(Math.Sqrt(L));
if ((l & 1) == 0)
l++;
r = (int)Math.Floor(Math.Sqrt(R));
if ((r & 1) == 0)
r--;
n1 = (int)Math.Floor((float)l / 2);
n2 = (int)Math.Ceiling((float)r / 2);
s1 = n1 * ((4 * n1 * n1) - 1) / 3;
s2 = n2 * ((4 * n2 * n2) - 1) / 3;
return s2 - s1;
}
public static void Main()
{
int L = 1;
int R = 9;
Console.Write(findSum(L, R));
}
}
|
Javascript
<script>
function findSum(L, R)
{
if (L < 0 || R < 0 || L > R)
return -1;
let l, r, n1, n2, s1, s2;
l = Math.ceil(Math.sqrt(L));
if (!(l & 1))
l++;
r = Math.floor(Math.sqrt(R));
if (!(r & 1))
r--;
n1 = Math.floor(l / 2);
n2 = Math.ceil(r / 2);
s1 = n1 * ((4 * n1 * n1) - 1) / 3;
s2 = n2 * ((4 * n2 * n2) - 1) / 3;
return s2 - s1;
}
let L = 1;
let R = 9;
document.write(findSum(L, R));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...