Find Range Value of the Expression
Last Updated :
10 Mar, 2022
Given two integers L and R, the task is to calculate the value of the expression:
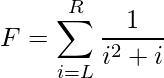
Examples:
Input: L = 6, R = 12
Output: 0.09
Input: L = 5, R = 6
Output: 0.06
Approach: It can be observed that 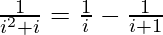 .
.
So, 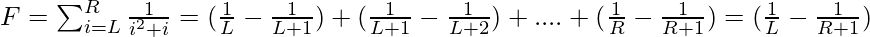
Hence, the answer will be (1 / L) – (1 / (R + 1)).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double get(double L, double R)
{
double x = 1.0 / L;
double y = 1.0 / (R + 1.0);
return (x - y);
}
int main()
{
int L = 6, R = 12;
double ans = get(L, R);
cout << fixed << setprecision(2) << ans;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static double get(double L, double R)
{
double x = 1.0 / L;
double y = 1.0 / (R + 1.0);
return (x - y);
}
public static void main(String []args)
{
int L = 6, R = 12;
double ans = get(L, R);
System.out.printf( "%.2f", ans);
}
}
|
Python3
def get(L, R) :
x = 1.0 / L;
y = 1.0 / (R + 1.0);
return (x - y);
if __name__ == "__main__" :
L = 6; R = 12;
ans = get(L, R);
print(round(ans, 2));
|
C#
using System;
public class GFG
{
static double get(double L, double R)
{
double x = 1.0 / L;
double y = 1.0 / (R + 1.0);
return (x - y);
}
public static void Main(String []args)
{
int L = 6, R = 12;
double ans = get(L, R);
Console.Write( "{0:F2}", ans);
}
}
|
Javascript
<script>
function get(L, R)
{
let x = 1.0 / L;
let y = 1.0 / (R + 1.0);
return (x - y);
}
let L = 6, R = 12;
let ans = get(L, R);
document.write(Math.round(ans * 100) / 100);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...