Find position of given term in a series formed with only digits 4 and 7 allowed

There is a series of numbers that have only digits, 4 and 7, and numbers are arranged in increasing order. The first few numbers of the series are 4, 7, 44, 47, 74, 77, 444, …etc. Given a number N, the task is to find the position of that number in the given series.
Examples:

Input: N = 4 
Output: 1 
Explanation:
The first number in the series is 4
Input: N = 777 
Output: 14 
Explanation:
The 14th number in the series is 777 

Approach: This problem can be solved using the below observations: 

• Below is the pattern observe in the given series. The numbers can be seen as: 
  

                 ""
              /      \
            4         7
          /   \     /   \ 
        44    47   74    77
       / \   / \   / \  / \

• As we can observe the pattern is increasing in power of 2. Therefore the idea is to iterate over the digits of the number starting from the least significant digit and update the position of the number as: 
  1. If current digit = 7, then add 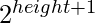to the position.
  2. If current digit = 4, then add 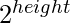to the position.
• Print the final position after the above operations.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the position
// of the number N
void findPosition(int n)
{
    int i = 0;

    // To store the position of N
    int pos = 0;

    // Iterate through all digit of N
    while (n > 0) {

        // If current digit is 7
        if (n % 10 == 7) {
            pos = pos + pow(2, i + 1);
        }

        // If current digit is 4
        else {
            pos = pos + pow(2, i);
        }

        i++;
        n = n / 10;
    }

    // Print the final position
    cout << pos;
}

// Driver Code
int main()
{
    // Given number of the series
    int N = 777;

    // Function Call
    findPosition(N);
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
class GFG{

// Function to find the position
// of the number N
static void findPosition(int n)
{
    int i = 0;

    // To store the position of N
    int pos = 0;

    // Iterate through all digit of N
    while (n > 0)
    {

        // If current digit is 7
        if (n % 10 == 7)
        {
            pos = pos + (int)Math.pow(2, i + 1);
        }

        // If current digit is 4
        else
        {
            pos = pos + (int)Math.pow(2, i);
        }

        i++;
        n = n / 10;
    }

    // Print the final position
    System.out.print(pos);
}

// Driver Code
public static void main(String[] args)
{
    // Given number of the series
    int N = 777;

    // Function Call
    findPosition(N);
}
}

// This code is contributed by shivanisinghss2110

Python3

# Python3 program for the above approach

# Function to find the position
# of the number N
def findPosition(n):

    i = 0

    # To store the position of N
    pos = 0

    # Iterate through all digit of N
    while (n > 0):

        # If current digit is 7
        if (n % 10 == 7):
            pos = pos + pow(2, i + 1)

        # If current digit is 4
        else:
            pos = pos + pow(2, i)

        i += 1
        n = n // 10

    # Print the final position
    print(pos)

# Driver Code
if __name__ == '__main__':

    # Given number of the series
    N = 777

    # Function Call
    findPosition(N)

# This code is contributed by mohit kumar 29

C#

// C# program for the above approach
using System;
class GFG{

// Function to find the position
// of the number N
static void findPosition(int n)
{
    int i = 0;

    // To store the position of N
    int pos = 0;

    // Iterate through all digit of N
    while (n > 0)
    {

        // If current digit is 7
        if (n % 10 == 7)
        {
            pos = pos + (int)Math.Pow(2, i + 1);
        }

        // If current digit is 4
        else
        {
            pos = pos + (int)Math.Pow(2, i);
        }

        i++;
        n = n / 10;
    }

    // Print the final position
    Console.Write(pos);
}

// Driver Code
public static void Main()
{
    // Given number of the series
    int N = 777;

    // Function Call
    findPosition(N);
}
}

// This code is contributed by Code_Mech

Javascript

<script>
// javascript program for the above approach

    // Function to find the position
    // of the number N
    function findPosition(n)
    {
        var i = 0;

        // To store the position of N
        var pos = 0;

        // Iterate through all digit of N
        while (n > 0) {

            // If current digit is 7
            if (n % 10 == 7) {
                pos = pos + parseInt( Math.pow(2, i + 1));
            }

            // If current digit is 4
            else {
                pos = pos + parseInt( Math.pow(2, i));
            }

            i++;
            n = parseInt(n / 10);
        }

        // Print  the final position
        document.write(pos);
    }

    // Driver Code

    // Given number of the series
    var N = 777;

    // Function Call
    findPosition(N);

// This code is contributed by Princi Singh
</script>

Output:

14

Time Complexity: O(log₁₀N * log₂N), where N represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.