Find permutation with maximum remainder Sum
Last Updated :
27 Jul, 2023
Given an integer N, the task is to find a permutation of the integers from 1 to N such that 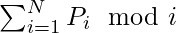 is maximum.
is maximum.
Examples:
Input: N = 3
Output: 3 1 2
Sum of the remainder values is (0 + 1 + 2) = 3
which is the maximum possible.
Input: N = 5
Output: 5 1 2 3 4
Approach:
As it is known that the maximum value of a number X after doing the mod with Y is Y-1. The permutation that will yield the maximum sum of the modulus values will be {N, 1, 2, 3, …., N – 1}. After evaluating the expression 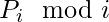 on the above array the output array will be {0, 1, 2, 3, …., N – 1} and this is the maximum value that can be obtained.
on the above array the output array will be {0, 1, 2, 3, …., N – 1} and this is the maximum value that can be obtained.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> Findpermutation(int n)
{
vector<int> a(n + 1);
a[1] = n;
for (int i = 2; i <= n; i++)
a[i] = i - 1;
return a;
}
int main()
{
int n = 8;
vector<int> v = Findpermutation(n);
for (int i = 1; i <= n; i++)
cout << v[i] << ' ';
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int[] Findpermutation(int n)
{
int [] a = new int[n + 1];
a[1] = n;
for (int i = 2; i <= n; i++)
a[i] = i - 1;
return a;
}
public static void main(String[] args)
{
int n = 8;
int []v = Findpermutation(n);
for (int i = 1; i <= n; i++)
System.out.print(v[i] + " ");
}
}
|
Python3
def Findpermutation(n) :
a = [0] * (n + 1);
a[1] = n;
for i in range(2, n + 1) :
a[i] = i - 1;
return a;
if __name__ == "__main__" :
n = 8;
v = Findpermutation(n);
for i in range(1, n + 1) :
print(v[i], end = ' ');
|
C#
using System;
class GFG
{
static int[] Findpermutation(int n)
{
int [] a = new int[n + 1];
a[1] = n;
for (int i = 2; i <= n; i++)
a[i] = i - 1;
return a;
}
public static void Main(String[] args)
{
int n = 8;
int []v = Findpermutation(n);
for (int i = 1; i <= n; i++)
Console.Write(v[i] + " ");
}
}
|
Javascript
<script>
function Findpermutation(n)
{
let a = new Array(n + 1);
a[1] = n;
for (let i = 2; i <= n; i++)
a[i] = i - 1;
return a;
}
let n = 8;
let v = Findpermutation(n);
for (let i = 1; i <= n; i++)
document.write(v[i] + ' ');
</script>
|
Time Complexity: O(N), Space Complexity: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...