Find parent of given node in a Binary Tree with given postorder traversal
Last Updated :
15 Mar, 2023
Given two integers N and K where N denotes the height of a binary tree, the task is to find the parent of the node with value K in a binary tree whose postorder traversal is first

natural numbers
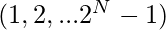
For N = 3, the Tree will be -
7
/ \
3 6
/ \ / \
1 2 4 5
Examples:
Input: N = 4, K = 5
Output: 6
Explanation:
Parent of the node 5 is 6. As shown in the tree above.
Input: N = 5, K = 3
Output: 7
Explanation:
Parent of the node 3 is 7. As shown in the tree above.
Naive Approach: A simple approach is to build the tree according to the following pattern and then traverse the whole tree to find the parent of a given node.
Efficient Approach: The idea is to use a binary search to find the parent of the node. As we know the binary Tree of Height N has

nodes. Therefore, the search space for the binary search will be 1 to

Now each node has children value either
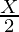
or
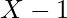
Therefore, parents of such nodes can be found easily.
Algorithm:
Step 1: Start
Step 2: Create a function called “findParent” that has two inputs: height and node. This function returns a number that represents the binary tree’s parent node for the specified node.
a. Set the initial values of the two variables “start” and “end” to 1 and 2height – 1, respectively.
b. Verify whether the specified node is the binary tree’s root node. Return -1 if the specified node is the root node because the root node has no parents.
c. Start a loop that keeps going until the specified node is discovered.
1. In the loop, as we ascend to the parent node, deduct 1 from the “end” variable.
2. Get the average of the “start” and “end” variables to determine the center node of the current range of nodes.
3. Verify whether the range’s final node or the intermediate node is the same as the specified node. Return the parent node that is equal to (end + 1) if either of the conditions is true.
4. Verify that the provided node is lower than the center node. If so, change the value of the “end” variable to the middle node.
5. If not, change the “start” variable such that it now represents the middle node.
6. If the specified node is not located, repeat steps 5–9 until it is.
7. Lastly, give the supplied node’s parent node back.
Step 3: End
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findParent(int height, int node)
{
int start = 1;
int end = pow(2, height) - 1;
if (end == node)
return -1;
while (node >= 1) {
end = end - 1;
int mid = start
+ (end - start)
/ 2;
if (mid == node || end == node) {
return (end + 1);
}
else if (node < mid) {
end = mid;
}
else {
start = mid;
}
}
}
int main()
{
int height = 4;
int node = 6;
int k = findParent(height, node);
cout << k;
return 0;
}
|
Java
import java.util.*;
class GFG{
static int findParent(int height,
int node)
{
int start = 1;
int end = (int)Math.pow(2, height) - 1;
if (end == node)
return -1;
while (node >= 1)
{
end = end - 1;
int mid = start + (end - start) / 2;
if (mid == node || end == node)
{
return (end + 1);
}
else if (node < mid)
{
end = mid;
}
else
{
start = mid;
}
}
return -1;
}
public static void main(String[] args)
{
int height = 4;
int node = 6;
int k = findParent(height, node);
System.out.print(k);
}
}
|
Python3
import math
def findParent(height, node):
start = 1
end = pow(2, height) - 1
if (end == node):
return -1
while(node >= 1):
end = end - 1
mid = start + (end - start)//2
if(mid == node or end == node):
return (end + 1)
elif (node < mid):
end = mid
else:
start = mid
if __name__ == "__main__":
height = 4
node = 6
k = findParent(height, node)
print(k)
|
C#
using System;
class GFG{
static int findParent(int height,
int node)
{
int start = 1;
int end = (int)Math.Pow(2, height) - 1;
if (end == node)
return -1;
while (node >= 1)
{
end = end - 1;
int mid = start + (end - start) / 2;
if (mid == node || end == node)
{
return (end + 1);
}
else if (node < mid)
{
end = mid;
}
else
{
start = mid;
}
}
return -1;
}
public static void Main(String[] args)
{
int height = 4;
int node = 6;
int k = findParent(height, node);
Console.Write(k);
}
}
|
Javascript
<script>
function findParent(height, node)
{
let start = 1;
let end = Math.pow(2, height) - 1;
if (end == node)
return -1;
while (node >= 1)
{
end = end - 1;
let mid = start + parseInt((end - start) / 2, 10);
if (mid == node || end == node)
{
return (end + 1);
}
else if (node < mid)
{
end = mid;
}
else
{
start = mid;
}
}
return -1;
}
let height = 4;
let node = 6;
let k = findParent(height, node);
document.write(k);
</script>
|
Time complexity: O(log n) where n is no of nodes in binary tree
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...