Skip to content
Related Articles
Open in App
Not now

Related Articles

Find a pair with given sum in BST

Improve Article
Save Article
Like Article
  • Difficulty Level : Medium
  • Last Updated : 21 Feb, 2023
Improve Article
Save Article
Like Article

Given a BST and a sum, find if there is a pair with the given sum.

Example:

Input: sum = 28, given BST

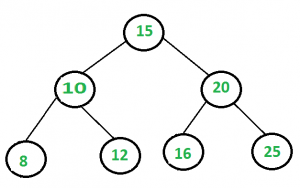
Output: Pair is found (16, 12)

Recommended: Please solve it on “PRACTICE” first, before moving on to the solution

Pair with given sum using Hashing

The idea is based on Hashing. We traverse binary search tree by inorder way and insert node’s value into a set. Also check for any node, difference between given sum and node’s value in set, if it is found then pair exists otherwise it doesn’t exist. 

Follow the steps mentioned below to implement the idea:

  • Traverse the tree, while traversing store the value of a node in the set
  • If for a current node with value x, there exists a y for which x + y = sum then check it using set and return the pair.

Below is the implementation of the above approach:

C++




// CPP program to find a pair with
// given sum using hashing
#include <bits/stdc++.h>
using namespace std;
 
struct Node {
    int data;
    struct Node *left, *right;
};
 
Node* NewNode(int data)
{
    Node* temp = (Node*)malloc(sizeof(Node));
    temp->data = data;
    temp->left = NULL;
    temp->right = NULL;
    return temp;
}
 
Node* insert(Node* root, int key)
{
    if (root == NULL)
        return NewNode(key);
    if (key < root->data)
        root->left = insert(root->left, key);
    else
        root->right = insert(root->right, key);
    return root;
}
 
bool findpairUtil(Node* root, int sum,
                  unordered_set<int>& set)
{
    if (root == NULL)
        return false;
 
    if (findpairUtil(root->left, sum, set))
        return true;
 
    if (set.find(sum - root->data) != set.end()) {
        cout << "Pair is found (" << sum - root->data
             << ", " << root->data << ")" << endl;
        return true;
    }
    else
        set.insert(root->data);
 
    return findpairUtil(root->right, sum, set);
}
 
void findPair(Node* root, int sum)
{
    unordered_set<int> set;
    if (!findpairUtil(root, sum, set))
        cout << "Pairs do not exit" << endl;
}
 
// Driver code
int main()
{
    Node* root = NULL;
    root = insert(root, 15);
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 8);
    root = insert(root, 12);
    root = insert(root, 16);
    root = insert(root, 25);
    root = insert(root, 10);
 
    int sum = 28;
    findPair(root, sum);
 
    return 0;
}

Java



// THIS CODE IS CONTRIBUTED BY YASH AGARWAL(YASHAGARWAL2852002)
// Java code to find a pair with given sum
// using hashing approach
import java.util.*;
 
public class GFG {
    // node class structure
    static class Node {
        int data;
        Node left, right;
    };
 
      // utility function that returns the new node
    static Node NewNode(int data){
        Node temp = new Node();
        temp.data = data;
        temp.left = null;
        temp.right = null;
        return temp;
    }
 
      // inserting node at correct position in BST
    static Node insert(Node root, int key){
        if (root == null) return NewNode(key);
        if (key < root.data) root.left = insert(root.left, key);
        else root.right = insert(root.right, key);
        return root;
    }
 
    static boolean findpairUtil(Node root, int sum, HashSet<Integer> set){
          // base case
        if (root == null) return false;
 
        if (findpairUtil(root.left, sum, set)) return true;
 
        if (set.contains(sum - root.data)){
            System.out.println("Pair is found (" + (sum - root.data) + ", " + root.data + ")");
            return true;
        }
        else set.add(root.data);
 
        return findpairUtil(root.right, sum, set);
    }
 
    static void findPair(Node root, int sum){
        HashSet<Integer> set = new HashSet<Integer>();
        if (!findpairUtil(root, sum, set))
            System.out.print("Pairs do not exit \n");
    }
 
    // Driver code to test above function
    public static void main(String[] args){
        Node root = null;
        root = insert(root, 15);
        root = insert(root, 10);
        root = insert(root, 20);
        root = insert(root, 8);
        root = insert(root, 12);
        root = insert(root, 16);
        root = insert(root, 25);
        root = insert(root, 10);
 
        int sum = 28;
        findPair(root, sum);
    }
}
Python3



# Python3 program to find a pair with
# given sum using hashing
import sys
import math
 
 
class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
 
def insert(root, data):
    if root is None:
        return Node(data)
    if(data < root.data):
        root.left = insert(root.left, data)
    if(data > root.data):
        root.right = insert(root.right, data)
    return root
 
 
def findPairUtil(root, summ, unsorted_set):
    if root is None:
        return False
    if findPairUtil(root.left, summ, unsorted_set):
        return True
    if unsorted_set and (summ-root.data) in unsorted_set:
        print("Pair is Found ({},{})".format(summ-root.data, root.data))
        return True
    else:
        unsorted_set.add(root.data)
 
    return findPairUtil(root.right, summ, unsorted_set)
 
 
def findPair(root, summ):
    unsorted_set = set()
    if(not findPairUtil(root, summ, unsorted_set)):
        print("Pair do not exist!")
 
 
# Driver code
if __name__ == '__main__':
    root = None
    root = insert(root, 15)
    root = insert(root, 10)
    root = insert(root, 20)
    root = insert(root, 8)
    root = insert(root, 12)
    root = insert(root, 16)
    root = insert(root, 25)
    root = insert(root, 10)
    summ = 28
    findPair(root, summ)
 
# This code is contributed by Vikash Kumar 37
C#



// C# program to find a pair with
// given sum using hashing
using System;
using System.Collections.Generic;
 
class GFG {
 
    class Node {
        public int data;
        public Node left, right;
    };
 
    static Node NewNode(int data)
    {
        Node temp = new Node();
        temp.data = data;
        temp.left = null;
        temp.right = null;
        return temp;
    }
 
    static Node insert(Node root, int key)
    {
        if (root == null)
            return NewNode(key);
        if (key < root.data)
            root.left = insert(root.left, key);
        else
            root.right = insert(root.right, key);
        return root;
    }
 
    static bool findpairUtil(Node root, int sum,
                             HashSet<int> set)
    {
        if (root == null)
            return false;
 
        if (findpairUtil(root.left, sum, set))
            return true;
 
        if (set.Contains(sum - root.data)) {
            Console.WriteLine("Pair is found ("
                              + (sum - root.data) + ", "
                              + root.data + ")");
            return true;
        }
        else
            set.Add(root.data);
 
        return findpairUtil(root.right, sum, set);
    }
 
    static void findPair(Node root, int sum)
    {
        HashSet<int> set = new HashSet<int>();
        if (!findpairUtil(root, sum, set))
            Console.Write("Pairs do not exit"
                          + "\n");
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        Node root = null;
        root = insert(root, 15);
        root = insert(root, 10);
        root = insert(root, 20);
        root = insert(root, 8);
        root = insert(root, 12);
        root = insert(root, 16);
        root = insert(root, 25);
        root = insert(root, 10);
 
        int sum = 28;
        findPair(root, sum);
    }
}
 
// This code is contributed by Rajput-Ji
Javascript



// JavaScript program to find a pair with
// given sum using hashing
class Node {
    constructor()
    {
        this.data = 0;
        this.left = null;
        this.right = null;
    }
};
function NewNode(data)
{
    var temp = new Node();
    temp.data = data;
    temp.left = null;
    temp.right = null;
    return temp;
}
function insert(root, key)
{
    if (root == null)
        return NewNode(key);
    if (key < root.data)
        root.left = insert(root.left, key);
    else
        root.right = insert(root.right, key);
    return root;
}
function findpairUtil(root, sum, set)
{
    if (root == null)
        return false;
    if (findpairUtil(root.left, sum, set))
        return true;
    if (set.has(sum - root.data)) {
        console.log("Pair is found ("
                          + (sum - root.data) + ", "
                          + root.data + ")<br>");
        return true;
    }
    else
        set.add(root.data);
    return findpairUtil(root.right, sum, set);
}
function findPair(root, sum)
{
    var set = new Set();
    if (!findpairUtil(root, sum, set))
        console.log("Pairs do not exit"
                      + "\n");
}
// Driver code
var root = null;
root = insert(root, 15);
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 8);
root = insert(root, 12);
root = insert(root, 16);
root = insert(root, 25);
root = insert(root, 10);
var sum = 28;
findPair(root, sum);
Output
Pair is found (12, 16)
Time Complexity: O(N)
Auxiliary Space: O(N)
Pair with a given sum using Two pointers
Key Idea:
The main idea is to find the Inorder Traversal of the BST and store it in a vector. We know that Inorder traversal of BST will be in sorted order.Now we will Apply Two pointers Technique to find that whether there exist two elements in the vector that sums up to the given value.
Algorithm:
1. First find the Inorder traversal of the Given BST and store it in a vector  (Let v).
2. Take two pointers i and j. Keep i at the start of v and j at the end of the v.  
   Now, if sum of elements at the ith index and jth index is greater that the given element then decrement j, 
   if sum of elements at the ith index and jth index is less that the given element then increment i,
    else, these two elements are our required answer. 
Below is the implementation of the above approach:
C++



#include <bits/stdc++.h>
using namespace std;
 
struct TreeNode {
    int val;
    struct TreeNode *left, *right;
};
 
TreeNode* NewNode(int data)
{
    TreeNode* temp = (TreeNode*)malloc(sizeof(TreeNode));
    temp->val = data;
    temp->left = NULL;
    temp->right = NULL;
    return temp;
}
 
TreeNode* insert(TreeNode* root, int key)
{
    if (root == NULL)
        return NewNode(key);
    if (key < root->val)
        root->left = insert(root->left, key);
    else
        root->right = insert(root->right, key);
    return root;
}
 
void inorder(TreeNode* root, vector<int>& v)
{
    if (root == NULL) {
        return;
    }
    inorder(root->left, v);
    v.push_back(root->val);
    inorder(root->right, v);
}
 
pair<int, int> findTarget(TreeNode* root, int k)
{
 
    vector<int> v;
    inorder(root, v);
    int n = v.size();
    int i = 0;
    int j = n - 1;
    while (j > i) {
        if (v[i] + v[j] == k) {
            return { v[i], v[j] };
        }
        else if (v[i] + v[j] > k) {
            j--;
        }
        else {
            i++;
        }
    }
    return { -1, -1 };
}
 
int main()
{
 
    TreeNode* root = NULL;
    root = insert(root, 15);
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 8);
    root = insert(root, 12);
    root = insert(root, 16);
    root = insert(root, 25);
    root = insert(root, 10);
 
    int k = 28;
 
    auto a = findTarget(root, k);
    cout << a.first << " " << a.second << endl;
}
Java



import java.util.*;
 
public class GFG {
 
  static class pair {
    int first, second;
    pair(int f, int s)
    {
      first = f;
      second = s;
    }
  }
  static class NewNode {
    int val;
    NewNode left, right;
 
    NewNode(int data)
    {
      val = data;
      left = null;
      right = null;
    }
  };
 
  static NewNode insert(NewNode root, int key)
  {
    if (root == null)
      return new NewNode(key);
    if (key < root.val)
      root.left = insert(root.left, key);
    else
      root.right = insert(root.right, key);
    return root;
  }
 
  static void inorder(NewNode root, ArrayList<Integer> v)
  {
    if (root == null) {
      return;
    }
    inorder(root.left, v);
    v.add(root.val);
    inorder(root.right, v);
  }
 
  static pair findTarget(NewNode root, int k)
  {
 
    ArrayList<Integer> v = new ArrayList<>();
    inorder(root, v);
    int n = v.size();
    int i = 0;
    int j = n - 1;
    while (j > i) {
      if (v.get(i) + v.get(j) == k) {
        return new pair(v.get(i), v.get(j));
      }
      else if (v.get(i) + v.get(j) > k) {
        j--;
      }
      else {
        i++;
      }
    }
    return new pair(-1, -1);
  }
 
  public static void main(String[] args)
  {
    NewNode root = null;
    root = insert(root, 15);
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 8);
    root = insert(root, 12);
    root = insert(root, 16);
    root = insert(root, 25);
    root = insert(root, 10);
 
    int k = 28;
 
    pair a = findTarget(root, k);
    System.out.println(a.first + " " + a.second);
  }
}
 
// This code is contributed by Karandeep1234
Python3



class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
 
def NewNode(data):
    temp = TreeNode(data)
    return temp
 
def insert(root, key):
    if root is None:
        return NewNode(key)
    if key < root.val:
        root.left = insert(root.left, key)
    else:
        root.right = insert(root.right, key)
    return root
 
def inorder(root, v):
    if root is None:
        return
    inorder(root.left, v)
    v.append(root.val)
    inorder(root.right, v)
 
def findTarget(root, k):
    v = []
    inorder(root, v)
    n = len(v)
    i = 0
    j = n - 1
    while j > i:
        if v[i] + v[j] == k:
            return (v[i], v[j
    ])
        elif v[i] + v[j] > k:
            j -= 1
        else:
            i += 1
    return (-1, -1)
 
if __name__ == '__main__':
    root = None
    root = insert(root, 15)
    root = insert(root, 10)
    root = insert(root, 20)
    root = insert(root, 8)
    root = insert(root, 12)
    root = insert(root, 16)
    root = insert(root, 25)
    root = insert(root, 10)
 
    k = 28
 
    a = findTarget(root, k)
    print(a[0], a[1])
C#



using System;
using System.Collections.Generic;
 
public class GFG
{
  public class pair
  {
    public int first, second;
    public pair(int f, int s)
    {
      first = f;
      second = s;
    }
  }
  public class NewNode
  {
    public int val;
    public NewNode left, right;
    public NewNode(int data)
    {
      val = data;
      left = null;
      right = null;
    }
  };
 
  public static NewNode insert(NewNode root, int key)
  {
    if (root == null)
      return new NewNode(key);
    if (key < root.val)
      root.left = insert(root.left, key);
    else
      root.right = insert(root.right, key);
    return root;
  }
 
  public static void inorder(NewNode root, List<int> v)
  {
    if (root == null)
    {
      return;
    }
    inorder(root.left, v);
    v.Add(root.val);
    inorder(root.right, v);
  }
 
  public static pair findTarget(NewNode root, int k)
  {
 
    List<int> v = new List<int>();
    inorder(root, v);
    int n = v.Count;
    int i = 0;
    int j = n - 1;
    while (j > i)
    {
      if (v[i] + v[j] == k)
      {
        return new pair(v[i], v[j]);
      }
      else if (v[i] + v[j] > k)
      {
        j--;
      }
      else
      {
        i++;
      }
    }
    return new pair(-1, -1);
  }
 
  public static void Main (String[] args)
  {
    NewNode root = null;
    root = insert(root, 15);
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 8);
    root = insert(root, 12);
    root = insert(root, 16);
    root = insert(root, 25);
    root = insert(root, 10);
 
    int k = 28;
 
    pair a = findTarget(root, k);
    Console.WriteLine(a.first + " " + a.second);
  }
}
 
// This code is contributed by Ajax
Javascript



class TreeNode {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}
 
function NewNode(data) {
    let temp = new TreeNode(data);
    return temp;
}
 
function insert(root, key) {
    if (root === null) {
        return NewNode(key);
    }
    if (key < root.val) {
        root.left = insert(root.left, key);
    } else {
        root.right = insert(root.right, key);
    }
    return root;
}
 
function inorder(root, v) {
    if (root === null) {
        return;
    }
    inorder(root.left, v);
    v.push(root.val);
    inorder(root.right, v);
}
 
function findTarget(root, k) {
    let v = [];
    inorder(root, v);
    let n = v.length;
    let i = 0;
    let j = n - 1;
    while (j > i) {
        if (v[i] + v[j] === k) {
            return [v[i], v[j]];
        } else if (v[i] + v[j] > k) {
            j -= 1;
        } else {
            i += 1;
        }
    }
    return [-1, -1];
}
 
let root = null;
root = insert(root, 15);
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 8);
root = insert(root, 12);
root = insert(root, 16);
root = insert(root, 25);
root = insert(root, 10);
 
let k = 28;
 
let a = findTarget(root, k);
console.log(a[0], a[1]);
Output
8 20
Time Complexity: O(n) (n = number of nodes)
Auxiliary Space: O(n)
    

My Personal Notes
arrow_drop_up
Like Article

Save Article

Related Articles
1.
Find a pair with given sum in a Balanced BST
2.
Find k-th smallest element in BST (Order Statistics in BST)
3.
Pair with a given sum in BST | Set 2
4.
Convert a normal BST to Balanced BST
5.
Two nodes of a BST are swapped, correct the BST
6.
K'th Largest Element in BST when modification to BST is not allowed
7.
Pair with given product | Set 1 (Find if any pair exists)
8.
Pair with minimum absolute difference in BST
9.
Find all the pairs with given sum in a BST | Set 2
10.
Pair formation such that maximum pair sum is minimized
Previous
Inorder Successor in Binary Search Tree
Next

Maximum element between two nodes of BST
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
aditya1011
@aditya1011
Vote for difficulty
Current difficulty :
Medium





Improved By :
Article Tags :
Practice Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox

Start Your Coding Journey Now!