Find number of subarrays ending with arr[i] where arr[i] is the minimum element of that subarray

Given an array, arr[] of size N, the task is to find the number of sub-arrays ending with arr[i] and arr[i] is the minimum element of that sub-array. 
Examples:

Input: arr[] = {3, 1, 2, 4} 
Output: 1 2 1 1 
Explanation:
Subarrays ending with 3 where 3 is the minimum element = {3} 
Subarrays ending with 1 where 1 is the minimum element = {3, 1}, {1} 
Subarrays ending with 2 where 2 is the minimum element = {2} 
Subarrays ending with 4 where 4 is the minimum element = {4}
Input: arr[] = {5, 4, 3, 2, 1} 
Output: 1 2 3 4 5 

Approach: The idea is to use the approach used to find Next Greater Element by maintaining a stack. Step-wise approach for the problem is: 

• Push the first element (arr[0]) of the array with count as 1 in the stack because first element will be the sub-array itself ending with current element arr[0] and minimum of the subarray
• Then for each element arr[i] in the array- 
  1. Pop the elements from the stack until the top of the stack is greater than the current element and add the count of the popped element in the count of current element.
  2. Push current element and the count as a pair in the stack.

For example: For arr[] = {3, 1, 2, 4}, 

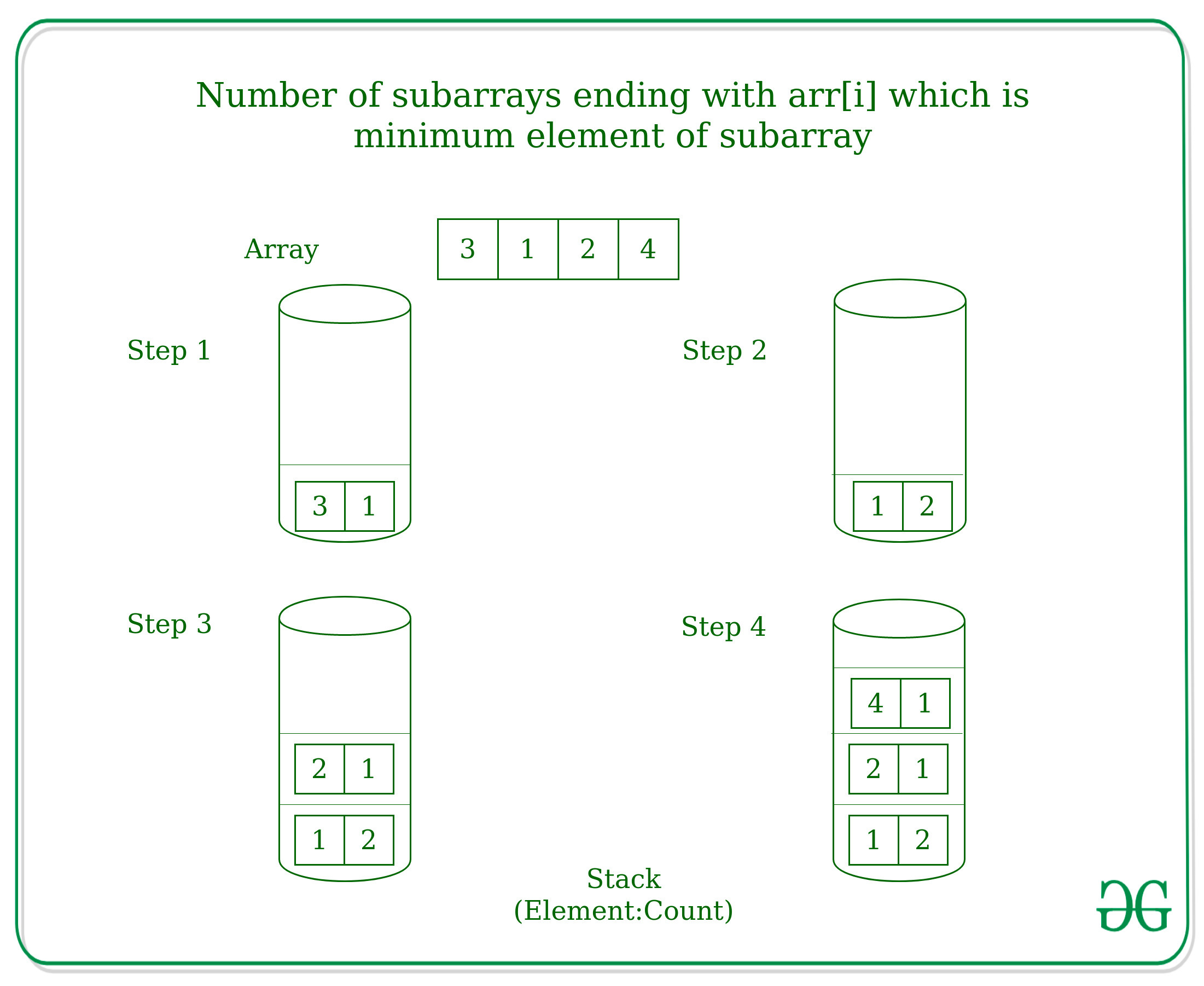
Below is the implementation of the above approach:

C++

// C++ implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray

#include <bits/stdc++.h>
using namespace std;

// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
int min_subarray(int a[], int n)
{
    stack<pair<int, int> > st;

    for (int i = 0; i < n; ++i) {

        // There exists a subarray of
        // size 1 for each element
        int count = 1;

        // Remove all greater elements
        while (!st.empty() &&
               st.top().first > a[i]) {

            // Increment the count
            count += st.top().second;

            // Remove the element
            st.pop();
        }

        // Push the current element
        // and it's count
        st.push({ a[i], count });

        cout << count << " ";
    }
}

// Driver Code
int main()
{
    int a[] = {5, 4, 3, 2, 1};
    int n = sizeof(a) / sizeof(a[0]);

    min_subarray(a, n);

    return 0;
}

Java

// Java implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
    static class Pair
    {
        int first;
        int second;
        public Pair(int x, int y)
        {
            this.first = x;
            this.second = y;
        }
    }

// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
static void min_subarray(int []a, int n)
{
    Stack<Pair> st = new Stack<Pair>();

    for (int i = 0; i < n; ++i)
    {

        // There exists a subarray of
        // size 1 for each element
        int count = 1;

        // Remove all greater elements
        while (st.empty() == false &&
            st.peek().first > a[i])
        {

            // Increment the count
            count += st.peek().second;

            // Remove the element
            st.pop();
        }

        // Push the current element
        // and it's count
        st.push(new Pair (a[i], count ));

        System.out.print(count + " ");
    }
}

// Driver Code
public static void main(String []args)
{
    int []a = {5, 4, 3, 2, 1};
    int n = a.length;

    min_subarray(a, n);
}
}

// This code is contributed by tufan_gupta2000

Python3

# Python3 implementation to find the number
# of sub-arrays ending with arr[i] which
# is the minimum element of the subarray

# Function to find the number
# of sub-arrays ending with arr[i] which
# is the minimum element of the subarray
def min_subarray(a, n) :

    st = [];

    for i in range(n) :

        # There exists a subarray of
        # size 1 for each element
        count = 1;

        # Remove all greater elements
        while len(st) != 0 and st[-1][0] > a[i] :

            # Increment the count
            count += st[-1][1];

            # Remove the element
            st.pop();

        # Push the current element
        # and it's count
        st.append(( a[i], count ));

        print(count,end= " ");

# Driver Code
if __name__ == "__main__" :

    a = [5, 4, 3, 2, 1];
    n = len(a);

    min_subarray(a, n);

# This code is contributed by AnkitRai01

C#

// C# implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
using System;
using System.Collections.Generic;

class GFG
{
    class Pair
    {
        public int first;
        public int second;
        public Pair(int x, int y)
        {
            this.first = x;
            this.second = y;
        }
    }

// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
static void min_subarray(int []a, int n)
{
    Stack<Pair> st = new Stack<Pair>();

    for (int i = 0; i < n; ++i)
    {

        // There exists a subarray of
        // size 1 for each element
        int count = 1;

        // Remove all greater elements
        while (st.Count != 0 &&
            st.Peek().first > a[i])
        {

            // Increment the count
            count += st.Peek().second;

            // Remove the element
            st.Pop();
        }

        // Push the current element
        // and it's count
        st.Push(new Pair (a[i], count ));

        Console.Write(count + " ");
    }
}

// Driver Code
public static void Main(String []args)
{
    int []a = {5, 4, 3, 2, 1};
    int n = a.Length;

    min_subarray(a, n);
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// Javascript implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray

// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
function min_subarray(a, n)
{
    var st = [];

    for (var i = 0; i < n; ++i) {

        // There exists a subarray of
        // size 1 for each element
        var count = 1;

        // Remove all greater elements
        while (st.length!=0 &&
               st[st.length-1][0] > a[i]) {

            // Increment the count
            count += st[st.length-1][1];

            // Remove the element
            st.pop();
        }

        // Push the current element
        // and it's count
        st.push([a[i], count]);

        document.write( count + " ");
    }
}

// Driver Code
var a = [5, 4, 3, 2, 1];
var n = a.length;
min_subarray(a, n);

// This code is contributed by itsok.
</script>

Output:

1 2 3 4 5

Time Complexity : O(n) ,where n is size of given array.

Space Complexity : O(n)