Find nth term of a given recurrence relation
Last Updated :
04 Aug, 2022
Let an be a sequence of numbers, which is defined by the recurrence relation a1=1 and an+1/an=2n. The task is to find the value of log2(an) for a given n.
Examples:
Input: 5
Output: 10
Explanation:
log2(an) = (n * (n - 1)) / 2
= (5*(5-1))/2
= 10
Input: 100
Output: 4950
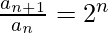
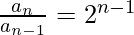
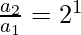 ,
,
We multiply all of the above in order to reach

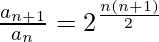
Since 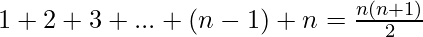 .
.
Then, 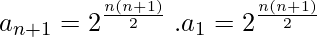
Substituting n+1 for n: 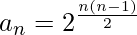
So, log_{2}(a_{n})=\frac{n(n-1)}{2}
Below is the implementation of the above approach as follows:
C++
#include <bits/stdc++.h>
using namespace std;
int sum(int n)
{
int ans = (n * (n - 1)) / 2;
return ans;
}
int main()
{
int n = 5;
cout << sum(n);
return 0;
}
|
Java
import java.util.*;
class solution
{
static int sum(int n)
{
int ans = (n * (n - 1)) / 2;
return ans;
}
public static void main(String arr[])
{
int n = 5;
System.out.println(sum(n));
}
}
|
Python3
def sum(n):
ans = (n * (n - 1)) / 2;
return ans
n = 5
print(int(sum(n)))
|
C#
using System;
class GFG
{
static int sum(int n)
{
int ans = (n * (n - 1)) / 2;
return ans;
}
public static void Main()
{
int n = 5;
Console.WriteLine(sum(n));
}
}
|
PHP
<?php
function sum($n)
{
$ans = ($n * ($n - 1)) / 2;
return $ans;
}
$n = 5;
echo sum($n);
?>
|
Javascript
<script>
function sum(n)
{
let ans = parseInt((n * (n - 1)) / 2);
return ans;
}
let n = 5;
document.write(sum(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1) // Because using constant variables
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...