Find if neat arrangement of cups and shelves can be made
Last Updated :
20 Feb, 2023
Given three different types of cups (a[]) and saucers (b[]), and n number of shelves, find if neat arrangement of cups and shelves can be made.
Arrangement of the cups and saucers will be neat if it follows the below rules:
- No shelf can contain both cups and saucers
- There can be no more than 5 cups in any shelf
- There can be no more than 10 saucers in any shelf
Examples:
Input : a[] = {3, 2, 6}, b[] = {4, 8, 9}, n = 10
Output : Yes
Explanation :
Total cups = 11, shelves required = 3
Total saucers = 21, shelves required = 3
Total required shelves = 3 + 3 = 6,
which is less than given number of shelves n. So, output is Yes.
Input : a[] = {4, 7, 4}, b[] = {3, 9, 10}, n = 2
Output : No
Approach: To arrange the cups and the saucers, find out the total number of cups 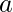 and total number of saucers
and total number of saucers 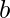 . Since, there cannot be more than 5 cups on the same shelf, therefore find out the maximum number of shelves required for cup by the formula
. Since, there cannot be more than 5 cups on the same shelf, therefore find out the maximum number of shelves required for cup by the formula 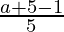 and the maximum number of shelves required for saucers by using the formula
and the maximum number of shelves required for saucers by using the formula 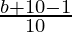 . If sum of these two values is equal to or less than
. If sum of these two values is equal to or less than 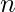 then the arrangement is possible otherwise not.
then the arrangement is possible otherwise not.
Below is the implementation of above approach :
C++
#include<bits/stdc++.h>
using namespace std;
void canArrange(int a[], int b[], int n)
{
int suma = 0, sumb = 0;
for(int i = 0; i < 3; i++)
suma += a[i];
for(int i = 0; i < 3; i++)
sumb += b[i];
int na = (suma + 5 - 1) / 5;
int nb = (sumb + 10 - 1) / 10;
if(na + nb <= n)
cout << "Yes";
else
cout << "No";
}
int main()
{
int a[] = {3, 2, 6};
int b[] = {4, 8, 9};
int n = 10;
canArrange(a, b, n);
return 0;
}
|
Java
import java.io.*;
class Gfg
{
public static void canArrange(int a[], int b[],
int n)
{
int suma = 0, sumb = 0;
for(int i = 0; i < 3; i++)
suma += a[i];
for(int i = 0; i < 3; i++)
sumb += b[i];
int na = (suma + 5 - 1) / 5;
int nb = (sumb + 10 - 1) / 10;
if(na + nb <= n)
System.out.println("Yes");
else
System.out.println("No");
}
public static void main(String args[])
{
int a[] = {3, 2, 6};
int b[] = {4, 8, 9};
int n = 10;
canArrange(a, b, n);
}
}
|
Python 3
import math
def canArrange( a, b, n):
suma = 0
sumb = 0
for i in range(0, len(a)):
suma += a[i]
for i in range(0,len(b)):
sumb += b[i]
na = (suma + 5 - 1) / 5
nb = (sumb + 10 - 1) / 10
if(na + nb <= n):
print("Yes")
else:
print("No")
a = [3, 2, 6]
b = [4, 8, 9]
n = 10
canArrange(a ,b ,n)
|
C#
using System;
class Gfg {
public static void canArrange(int []a, int []b,
int n)
{
int suma = 0, sumb = 0;
for(int i = 0; i < 3; i++)
suma += a[i];
for(int i = 0; i < 3; i++)
sumb += b[i];
int na = (suma + 5 - 1) / 5;
int nb = (sumb + 10 - 1) / 10;
if(na + nb <= n)
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
public static void Main()
{
int []a = {3, 2, 6};
int []b = {4, 8, 9};
int n = 10;
canArrange(a, b, n);
}
}
|
PHP
<?php
function canArrange($a, $b, $n)
{
$suma = 0; $sumb = 0;
for( $i = 0; $i < 3; $i++)
$suma += $a[$i];
for( $i = 0; $i < 3; $i++)
$sumb += $b[$i];
$na = ($suma + 5 - 1) / 5;
$nb = ($sumb + 10 - 1) / 10;
if($na + $nb <= $n)
echo "Yes";
else
echo "No";
}
$a = array(3, 2, 6);
$b = array(4, 8, 9);
$n = 10;
canArrange($a, $b, $n);
?>
|
Javascript
<script>
function canArrange( a, b, n)
{
let suma = 0, sumb = 0;
for(let i = 0; i < 3; i++)
suma += a[i];
for(let i = 0; i < 3; i++)
sumb += b[i];
let na = Math.floor((suma + 5 - 1)/5);
let nb = Math.floor((sumb + 10 - 1)/10);
if(na + nb <= n)
document.write("Yes");
else
document.write("No");
}
let a = [3, 2, 6];
let b = [4, 8, 9];
let n = 10;
canArrange(a, b, n);
</script>
|
Time complexity: O(1)
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...