Find n-th element from Stern’s Diatomic Series
Last Updated :
10 Dec, 2022
Given an integer n. we have to find the nth term of Stern’s Diatomic Series.
Stern’s diatomic series is the sequence which generates the following integer sequence 0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, ……. It arises in the Calkin-Wilf tree. It is sometimes also known as the fusc function.
In mathematical terms, the sequence P(n) of Stern’s diatomic series is defined by the recurrence relation.
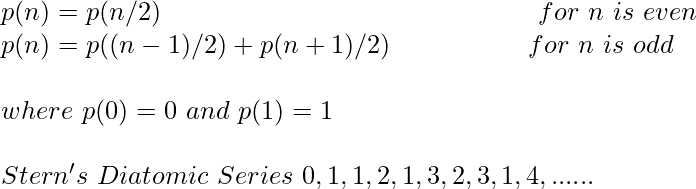
Examples :
Input : n = 7
Output : 3
Input : n = 15
Output : 4
Approach :
We solve this problem with a very simple concept of Dynamic programming which is used in finding fibonacci numbers. After saving the base case of DP[0] = 0, DP[1] = 1, we have to simply traverse from i = 2 to n and compute DP[i] as per explained definition of Stern’s diatomic series. And finally return the value of DP[n].
Algorithm :
// SET the Base case
DP[0] = 0;
DP[1] = 1;
// Traversing the array from 2nd Element to nth Element
for (int i=2; i<=n; i++)
{
// Case 1: for even n
if (i%2 == 0)
DP[i] = DP[i/2];
// Case 2: for odd n
else
DP[i] = DP[(i-1)/2] + DP[(i+1)/2];
}
return DP[n];
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findSDSFunc(int n)
{
int DP[n+1];
DP[0] = 0;
DP[1] = 1;
for (int i = 2; i <= n; i++) {
if (i % 2 == 0)
DP[i] = DP[i / 2];
else
DP[i] = DP[(i - 1) / 2] +
DP[(i + 1) / 2];
}
return DP[n];
}
int main()
{
int n = 15;
cout << findSDSFunc(n) << endl;
return 0;
}
|
Java
class GFG {
static int findSDSFunc(int n)
{
int DP[] = new int[n+1];
DP[0] = 0;
DP[1] = 1;
for (int i = 2; i <= n; i++)
{
if (i % 2 == 0)
DP[i] = DP[i / 2];
else
DP[i] = DP[(i - 1) / 2] +
DP[(i + 1) / 2];
}
return DP[n];
}
public static void main(String[] args)
{
int n = 15;
System.out.println(findSDSFunc(n));
}
}
|
Python 3
def findSDSFunc(n):
DP = [0] * (n+1)
DP[0] = 0
DP[1] = 1
for i in range(2, n+1):
if (int(i % 2) == 0):
DP[i] = DP[int(i / 2)]
else:
DP[i] = (DP[int((i - 1) / 2)]
+ DP[int((i + 1) / 2)])
return DP[n]
n = 15
print(findSDSFunc(n))
|
C#
using System;
class GFG
{
static int findSDSFunc(int n)
{
int []DP = new int[n + 1];
DP[0] = 0;
DP[1] = 1;
for (int i = 2; i <= n; i++)
{
if (i % 2 == 0)
DP[i] = DP[i / 2];
else
DP[i] = DP[(i - 1) / 2] +
DP[(i + 1) / 2];
}
return DP[n];
}
static public void Main ()
{
int n = 15;
Console.WriteLine(findSDSFunc(n));
}
}
|
PHP
<?php
function findSDSFunc($n)
{
$DP[0] = 0;
$DP[1] = 1;
for ($i = 2; $i <= $n; $i++)
{
if ($i % 2 == 0)
$DP[$i] = $DP[$i / 2];
else
$DP[$i] = $DP[($i - 1) / 2] +
$DP[($i + 1) / 2];
}
return $DP[$n];
}
$n = 15;
echo(findSDSFunc($n));
?>
|
Javascript
<script>
function findSDSFunc(n)
{
let DP = [];
DP[0] = 0;
DP[1] = 1;
for (let i = 2; i <= n; i++)
{
if (i % 2 == 0)
DP[i] = DP[i / 2];
else
DP[i] = DP[(i - 1) / 2] +
DP[(i + 1) / 2];
}
return DP[n];
}
let n = 15;
document.write(findSDSFunc(n));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...