Find the Missing Point of Parallelogram
Last Updated :
03 Aug, 2022
Given three coordinate points A, B and C, find the missing point D such that ABCD can be a parallelogram.
Examples :
Input : A = (1, 0)
B = (1, 1)
C = (0, 1)
Output : 0, 0
Explanation:
The three input points form a unit
square with the point (0, 0)
Input : A = (5, 0)
B = (1, 1)
C = (2, 5)
Output : 6, 4
As shown in below diagram, there can be multiple possible outputs, we need to print any one of them.
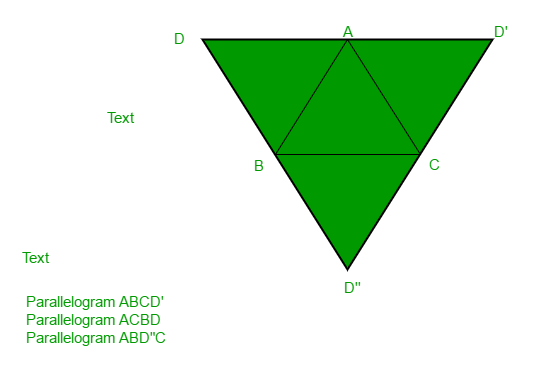
A quadrilateral is said to be a parallelogram if its opposite sides are parallel and equal in length.
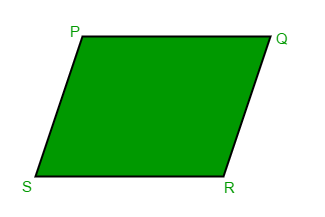
As we’re given three points of the parallelogram, we can find the slope of the missing sides as well as their lengths.
The algorithm can be explained as follows
Let R be the missing point. Now from definition, we have
- Length of PR = Length of QS = L1 (Opposite sides are equal)
- Slope of PR = Slope of QS = M1 (Opposite sides are parallel)
- Length of PQ = Length of RS = L2 (Opposite sides are equal)
- Slope of PQ= Slope of RS = M2 (Opposite sides are parallel)
Thus we can find the points at a distance L1 from P having slope M1 as mentioned in below article :
Find points at a given distance on a line of given slope.
Now one of the points will satisfy the above conditions which can easily be checked (using either condition 3 or 4)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Point {
float x, y;
Point()
{
x = y = 0;
}
Point(float a, float b)
{
x = a, y = b;
}
};
pair<Point, Point> findPoints(Point source,
float m, float l)
{
Point a, b;
if (m == 0) {
a.x = source.x + l;
a.y = source.y;
b.x = source.x - l;
b.y = source.y;
}
else if (m == std::numeric_limits<float>::max()) {
a.x = source.x;
a.y = source.y + l;
b.x = source.x;
b.y = source.y - l;
}
else {
float dx = (l / sqrt(1 + (m * m)));
float dy = m * dx;
a.x = source.x + dx, a.y = source.y + dy;
b.x = source.x - dx, b.y = source.y - dy;
}
return pair<Point, Point>(a, b);
}
float findSlope(Point p, Point q)
{
if (p.y == q.y)
return 0;
if (p.x == q.x)
return std::numeric_limits<float>::max();
return (q.y - p.y) / (q.x - p.x);
}
float findDistance(Point p, Point q)
{
return sqrt(pow((q.x - p.x), 2) + pow((q.y - p.y), 2));
}
void findMissingPoint(Point a, Point b, Point c)
{
pair<Point, Point> d = findPoints(a, findSlope(b, c),
findDistance(b, c));
if (findDistance(d.first, c) == findDistance(a, b))
cout << d.first.x << ", " << d.first.y << endl;
else
cout << d.second.x << ", " << d.second.y << endl;
}
int main()
{
findMissingPoint(Point(1, 0), Point(1, 1), Point(0, 1));
findMissingPoint(Point(5, 0), Point(1, 1), Point(2, 5));
return 0;
}
|
Java
import java.util.*;
class Point {
public double x, y;
public Point()
{
x = 0;
y = 0;
}
public Point(double a, double b)
{
x = a;
y = b;
}
};
class GFG {
static Point[] findPoints(Point source, double m,
double l)
{
Point a = new Point();
Point b = new Point();
if (m == 0) {
a.x = source.x + l;
a.y = source.y;
b.x = source.x - l;
b.y = source.y;
}
else if (m == Double.MAX_VALUE) {
a.x = source.x;
a.y = source.y + l;
b.x = source.x;
b.y = source.y - l;
}
else {
double dx = (l / Math.sqrt(1 + (m * m)));
double dy = m * dx;
a.x = source.x + dx;
a.y = source.y + dy;
b.x = source.x - dx;
b.y = source.y - dy;
}
Point[] res = { a, b };
return res;
}
static double findSlope(Point p, Point q)
{
if (p.y == q.y)
return 0;
if (p.x == q.x)
return Double.MAX_VALUE;
return (q.y - p.y) / (q.x - p.x);
}
static double findDistance(Point p, Point q)
{
return Math.sqrt(Math.pow((q.x - p.x), 2)
+ Math.pow((q.y - p.y), 2));
}
static void findMissingPoint(Point a, Point b, Point c)
{
Point[] d = findPoints(a, findSlope(b, c),
findDistance(b, c));
if (findDistance(d[0], c) == findDistance(a, b))
System.out.println(d[0].x + ", " + d[0].y);
else
System.out.println(d[1].x + ", " + d[1].y);
}
public static void main(String[] args)
{
findMissingPoint(new Point(1, 0), new Point(1, 1),
new Point(0, 1));
findMissingPoint(new Point(5, 0), new Point(1, 1),
new Point(2, 5));
}
}
|
Python3
import math as Math
FLOAT_MAX = 3.40282e+38
def findPoints(source, m, l):
a = [0] * (2)
b = [0] * (2)
if (m == 0):
a[0] = source[0] + l
a[1] = source[1]
b[0] = source[0] - l
b[1] = source[1]
elif (m == FLOAT_MAX):
a[0] = source[0]
a[1] = source[1] + l
b[0] = source[0]
b[1] = source[1] - l
else:
dx = (l / ((1 + (m * m)) ** 0.5))
dy = m * dx
a[0] = source[0] + dx
a[1] = source[1] + dy
b[0] = source[0] - dx
b[1] = source[1] - dy
return [a, b]
def findSlope(p, q):
if (p[1] == q[1]):
return 0
if (p[0] == q[0]):
return FLOAT_MAX
return (q[1] - p[1]) / (q[0] - p[0])
def findDistance(p, q):
return Math.sqrt(Math.pow((q[0] - p[0]), 2) + Math.pow((q[1] - p[1]), 2))
def findMissingPoint(a, b, c):
d = findPoints(a, findSlope(b, c), findDistance(b, c))
if (findDistance(d[0], c) == findDistance(a, b)):
print(f"{(int)(d[0][0])}, {(int)(d[0][1])}")
else:
print(f"{(int)(d[1][0])}, {(int)(d[1][1])}")
Point1 = [1, 0]
Point2 = [1, 1]
Point3 = [0, 1]
findMissingPoint(Point1, Point2, Point3)
Point1 = [5, 0]
Point2 = [1, 1]
Point3 = [2, 5]
findMissingPoint(Point1, Point2, Point3)
|
C#
using System;
using System.Collections.Generic;
class Point {
public double x, y;
public Point()
{
x = 0;
y = 0;
}
public Point(double a, double b)
{
x = a;
y = b;
}
};
class GFG
{
static Point[] findPoints(Point source, double m,
double l)
{
Point a = new Point();
Point b = new Point();
if (m == 0) {
a.x = source.x + l;
a.y = source.y;
b.x = source.x - l;
b.y = source.y;
}
else if (m == Double.MaxValue) {
a.x = source.x;
a.y = source.y + l;
b.x = source.x;
b.y = source.y - l;
}
else {
double dx = (l / Math.Sqrt(1 + (m * m)));
double dy = m * dx;
a.x = source.x + dx;
a.y = source.y + dy;
b.x = source.x - dx;
b.y = source.y - dy;
}
Point[] res = { a, b };
return res;
}
static double findSlope(Point p, Point q)
{
if (p.y == q.y)
return 0;
if (p.x == q.x)
return Double.MaxValue;
return (q.y - p.y) / (q.x - p.x);
}
static double findDistance(Point p, Point q)
{
return Math.Sqrt(Math.Pow((q.x - p.x), 2)
+ Math.Pow((q.y - p.y), 2));
}
static void findMissingPoint(Point a, Point b, Point c)
{
Point[] d = findPoints(a, findSlope(b, c),
findDistance(b, c));
if (findDistance(d[0], c) == findDistance(a, b))
Console.WriteLine(d[0].x + ", " + d[0].y);
else
Console.WriteLine(d[1].x + ", " + d[1].y);
}
public static void Main(string[] args)
{
findMissingPoint(new Point(1, 0), new Point(1, 1),
new Point(0, 1));
findMissingPoint(new Point(5, 0), new Point(1, 1),
new Point(2, 5));
}
}
|
Javascript
const FLOAT_MAX = 3.40282e+38;
function findPoints(source, m, l)
{
let a = new Array(2);
let b = new Array(2);
if (m == 0) {
a[0] = source[0] + l;
a[1] = source[1];
b[0] = source[0] - l;
b[1] = source[1];
}
else if (m == FLOAT_MAX) {
a[0] = source[0];
a[1] = source[1] + l;
b[0] = source[0];
b[1] = source[1] - l;
}
else {
let dx = (l / Math.sqrt(1 + (m * m)));
let dy = m * dx;
a[0] = source[0] + dx, a[1] = source[1] + dy;
b[0] = source[0] - dx, b[1] = source[1] - dy;
}
return [a, b];
}
function findSlope(p, q)
{
if (p[1] == q[1]){
return 0;
}
if (p[0] == q[0]){
return FLOAT_MAX;
}
return (q[1] - p[1]) / (q[0] - p[0]);
}
function findDistance(p, q)
{
return Math.sqrt(Math.pow((q[0] - p[0]), 2) + Math.pow((q[1] - p[1]), 2));
}
function findMissingPoint(a, b, c)
{
let d = findPoints(a, findSlope(b, c), findDistance(b, c));
if (findDistance(d[0], c) === findDistance(a, b)){
console.log(d[0][0], ",", d[0][1]);
}
else{
console.log(d[1][0], ",", d[1][1]);
}
}
{
let Point1 = [1, 0];
let Point2 = [1, 1];
let Point3 = [0, 1];
findMissingPoint(Point1, Point2, Point3);
Point1 = [5, 0];
Point2 = [1, 1];
Point3 = [2, 5];
findMissingPoint(Point1, Point2, Point3);
}
|
Output :
0, 0
6, 4
Time Complexity: O(log(log n)) since using inbuilt sqrt and log functions
Auxiliary Space: O(1)
Alternative Approach:
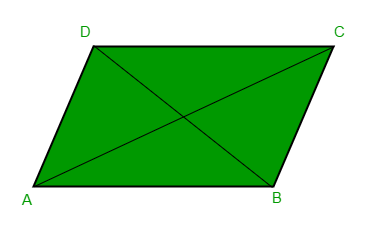
Since the opposite sides are equal, AD = BC and AB = CD, we can calculate the co-ordinates of the missing point (D) as:
AD = BC
(Dx - Ax, Dy - Ay) = (Cx - Bx, Cy - By)
Dx = Ax + Cx - Bx
Dy = Ay + Cy - By
References: https://math.stackexchange.com/questions/887095/find-the-4th-vertex-of-the-parallelogram
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int ax = 5, ay = 0;
int bx = 1, by = 1;
int cx = 2, cy = 5;
cout << ax + cx - bx << ", "
<< ay + cy - by;
return 0;
}
|
Java
import java.io.*;
class GFG
{
public static void main (String[] args)
{
int ax = 5, ay = 0;
int bx = 1, by = 1;
int cx = 2, cy = 5;
System.out.println(ax + (cx - bx) + ", " +
ay + (cy - by));
}
}
|
Python 3
if __name__ == "__main__":
ax, ay = 5, 0
bx ,by = 1, 1
cx ,cy = 2, 5
print(ax + cx - bx , ",", ay + cy - by)
|
C#
using System;
class GFG
{
static public void Main ()
{
int ax = 5, ay = 0;
int bx = 1, by = 1;
int cx = 2, cy = 5;
Console.WriteLine(ax + (cx - bx) + ", " +
ay + (cy - by));
}
}
|
PHP
<?php
$ax = 5;
$ay = 0;
$bx = 1;
$by = 1;
$cx = 2;
$cy = 5;
echo $ax + $cx - $bx , ", ",
$ay + $cy - $by;
?>
|
Javascript
<script>
let ax = 5, ay = 0;
let bx = 1, by = 1;
let cx = 2, cy = 5;
document.write((ax + (cx - bx)) + ", " + (ay + (cy - by)));
</script>
|
Output:
6, 4
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...