Find missing elements from an Array with duplicates

Given an array arr[] of size N having integers in the range [1, N] with some of the elements missing. The task is to find the missing elements.

Note: There can be duplicates in the array.

Examples:

Input: arr[] = {1, 3, 3, 3, 5}, N = 5
Output: 2 4
Explanation: The numbers missing from the list are 2 and 4
All other elements in the range [1, 5] are persent in the array.

Input: arr[] = {1, 2, 3, 4, 4, 7, 7}, N = 7
Output: 5 6

Approach 1(Negating visited elements): The idea to solve the problem is as follows

In the given range [1, N] there should be an element corresponding to each index. So mark the visited indices by multiplying that element with -1. If an element is missing then its index will have a positive element. Otherwise, it will have a negative element.  

Follow the below illustration:

Illustration:

Consider arr[] = {1, 3, ,3, 3, 5}
Here for illustration, we will use 1 based indexing

For i = 1:
        => arr[i] = 1. So mark arr[1] visited.
        => arr[1] = -1*arr[1] = -1*1 = -1
        => arr[] = {-1, 3, 3, 3, 5}

For i = 2:
        => arr[i] = 3. So mark arr[3] visited.
        => arr[3] = -1*arr[3] = -1*3 = -3
        => arr[] = {-1, 3, -3, 3, 5}

For i = 3:
        => arr[i] = -3. So we should move to absolute value of -3 i.e. 3
        => arr[3] is already visited. Skip to next index
        => arr[] = {-1, 3, -3, 3, 5}

For i = 4:
        => arr[i] = 3. So mark arr[3] visited.
        => arr[3] is already visited. Skip to next index
        => arr[] = {-1, 3, -3, 3, 5}

For i = 5:
        => arr[i] = 5. So mark arr[5] visited.
        => arr[5] = -1*arr[5] = -1*5 = -5
        => arr[] = {-1, 3, -3, 3, -5}

Again traverse the array. See that arr[2] and arr[4] are not visited.
So the missing elements are {2, 4}.

Follow the below steps to implement the idea:

• Traverse the array from i = 0 to N-1:
  • If the element is negative take the positive value (say x = abs(arr[i])).
  • if the value at (x-1)^th index is not visited i.e., it is still positive then multiply that element with -1.
• Traverse the array again from i = 0 to N-1:
  • If the element is not visited, i.e., has a positive value, push (i+1) to the resultant array.
• Return the resultant array that contains the missing elements.

Below is the implementation of the above approach:  

C++

// C++ implementation of the approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the missing elements
vector<int> missing_elements(vector<int> vec)
{
    // Vector to store the list
    // of missing elements
    vector<int> mis;

    // For every given element
    for (int i = 0; i < vec.size(); i++) {

        // Find its index
        int temp = abs(vec[i]) - 1;

        // Update the element at the found index
        vec[temp] = vec[temp] > 0
            ? -vec[temp] : vec[temp];
    }
    for (int i = 0; i < vec.size(); i++)

        // Current element was not present
        // in the original vector
        if (vec[i] > 0)
            mis.push_back(i + 1);

    return mis;
}

// Driver code
int main()
{
    vector<int> vec = { 3, 3, 3, 5, 1 };

    // Vector to store the returned
    // list of missing elements
    vector<int> miss_ele = missing_elements(vec);

    // Print the list of elements
    for (int i = 0; i < miss_ele.size(); i++)
        cout << miss_ele[i] << " ";
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

// C implementation of the approach

#include <stdio.h>
#include <stdlib.h>

// Function to find the missing elements
void missing_elements(int vec[], int n)
{
    int mis[n];
    for (int i = 0; i < n; i++)
        mis[i] = -1;

    // For every given element
    for (int i = 0; i < n; i++) {

        // Find its index
        int temp = abs(vec[i]) - 1;

        // Update the element at the found index
        vec[temp] = vec[temp] > 0 ? -vec[temp] : vec[temp];
    }
    // Current element was not present
    // in the original vector
    for (int i = 0; i < n; i++)
        if (vec[i] > 0)
            mis[i] = (i + 1);

    int miss_ele_size = sizeof(mis) / sizeof(mis[0]);
    for (int i = 0; i < miss_ele_size; i++) {
        if (mis[i] != -1)
            printf("%d ", mis[i]);
    }
}

// Driver code
int main()
{
    int vec[] = { 3, 3, 3, 5, 1 };
    int vec_size = sizeof(vec) / sizeof(vec[0]);
    missing_elements(vec, vec_size);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java implementation of the above approach

import java.util.*;

class GFG {

    // Function to find the missing elements
    static List<Integer>
    missing_elements(List<Integer> vec)
    {
        // Vector to store the list
        // of missing elements
        List<Integer> mis = new ArrayList<Integer>();

        // For every given element
        for (int i = 0; i < vec.size(); i++) {

            // Find its index
            int temp = Math.abs((int)vec.get(i)) - 1;

            // Update the element at the found index
            if ((int)vec.get(temp) > 0)
                vec.set(temp, -(int)vec.get(temp));
            else
                vec.set(temp, vec.get(temp));
        }
        for (int i = 0; i < vec.size(); i++) {

            // Current element was not present
            // in the original vector
            if ((int)vec.get(i) > 0)
                mis.add(i + 1);
        }
        return mis;
    }

    // Driver code
    public static void main(String args[])
    {
        List<Integer> vec = new ArrayList<Integer>();
        vec.add(3);
        vec.add(3);
        vec.add(3);
        vec.add(5);
        vec.add(1);

        // Vector to store the returned
        // list of missing elements
        List<Integer> miss_ele = missing_elements(vec);

        // Print the list of elements
        for (int i = 0; i < miss_ele.size(); i++)
            System.out.print(miss_ele.get(i) + " ");
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 implementation of the approach

# Function to find the missing elements


def missing_elements(vec):

    # Vector to store the list
    # of missing elements
    mis = []

    # For every given element
    for i in range(len(vec)):

        # Find its index
        temp = abs(vec[i]) - 1

        # Update the element at the found index
        if vec[temp] > 0:
            vec[temp] = -vec[temp]

    for i in range(len(vec)):

        # Current element was not present
        # in the original vector
        if (vec[i] > 0):
            mis.append(i + 1)

    return mis


# Driver code
if __name__ == '__main__':
    vec = [3, 3, 3, 5, 1]

    # Vector to store the returned
    # list of missing elements
    miss_ele = missing_elements(vec)

    # Print the list of elements
    for i in range(len(miss_ele)):
        print(miss_ele[i], end=" ")

# This code is contributed by Mohit Kumar

C#

// C# implementation of the approach

using System;
using System.Collections.Generic;

class GFG {

    // Function to find the missing elements
    static List<int> missing_elements(List<int> vec)
    {
        // List<int> to store the list
        // of missing elements
        List<int> mis = new List<int>();

        // For every given element
        for (int i = 0; i < vec.Count; i++) {

            // Find its index
            int temp = Math.Abs((int)vec[i]) - 1;

            // Update the element at the found index
            if ((int)vec[temp] > 0)
                vec[temp] = -(int)vec[temp];
            else
                vec[temp] = vec[temp];
        }
        for (int i = 0; i < vec.Count; i++) {

            // Current element was not present
            // in the original vector
            if ((int)vec[i] > 0)
                mis.Add(i + 1);
        }
        return mis;
    }

    // Driver code
    public static void Main(String[] args)
    {
        List<int> vec = new List<int>();
        vec.Add(3);
        vec.Add(3);
        vec.Add(3);
        vec.Add(5);
        vec.Add(1);

        // List to store the returned
        // list of missing elements
        List<int> miss_ele = missing_elements(vec);

        // Print the list of elements
        for (int i = 0; i < miss_ele.Count; i++)
            Console.Write(miss_ele[i] + " ");
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>

    // Javascript implementation of the approach

    // Function to find the missing elements
    function missing_elements(vec)
    {

        // Vector to store the list
        // of missing elements
        let mis = [];

        // For every given element
        for (let i = 0; i < vec.length; i++) {

            // Find its index
            let temp = Math.abs(vec[i]) - 1;

            // Update the element at the found index
            vec[temp] = vec[temp] > 0 ? -vec[temp] : vec[temp];
        }
        for (let i = 0; i < vec.length; i++)

            // Current element was not present
            // in the original vector
            if (vec[i] > 0)
                mis.push(i + 1);

        return mis;
    }

    let vec = [ 3, 3, 3, 5, 1 ];

    // Vector to store the returned
    // list of missing elements
    let miss_ele = missing_elements(vec);

    // Print the list of elements
    for (let i = 0; i < miss_ele.length; i++)
        document.write(miss_ele[i] + " ");

</script>

Output

2 4 

Time Complexity: O(N).
Auxiliary Space: O(N)

Approach 2 (Performing in-place sorting): The idea in this case, is to use in-place sorting. 

In the given range [1, N] there should be an element corresponding to each index. So we can sort them and then if at any index the position and the element are not same, those elements are missing.

For sorting the elements in linear time see the below pseudo code:

Pseudo Code:

Algorithm:
Start
        Set pointer i = 0
        while i < N:
                pos = arr[i] – 1
                If arr[pos] = pos + 1:  // the element is in the correct position
                        i++
                Else:  // swap it to correct position
                        swap(arr[pos], arr[i])
                end if
        end while
        for i = 0 to N-1:
                If Arr[i] = i+1:
                        continue
                Else: 
                        i+1 is missing.
                end if
        end for
End

Follow the illustration below for a better understanding:

Illustration:

Consider arr[] = {3, 3, 3, 5, 1}

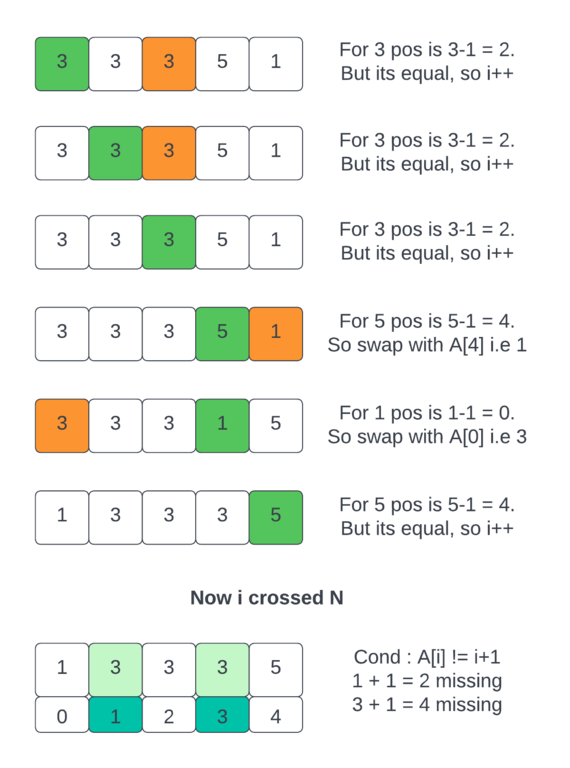
Example on how to sort in linear sort 

Below is the implementation of the above approach:  

C++

// C++ code ot implement the approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the missing elements
vector<int> FindMissing(vector<int> arr)
{
    int i = 0;
    int N = arr.size();
    while (i < N) {

        // as 0 based indxing
        int correct = arr[i] - 1;
        if (arr[i] != arr[correct]) {
            swap(arr[i], arr[correct]);
        }
        else {
            i++;
        }
    }

    vector<int> ans;
    for (i = 0; i < N; i++) {
        if (arr[i] != i + 1) {
            ans.push_back(i + 1);
        }
    }
    return ans;
}

// Driver code
int main()
{
    vector<int> arr = { 1, 3, 3, 3, 5 };

    // Function call
    vector<int> res = FindMissing(arr);
    for(int x: res)
        cout << x << " ";
    return 0;
}

// Code done by R.Balakrishnan (rbkraj000)

Output

2 4 

Time Complexity: O(N)
Even in the worst case, there will be N-1 Swaps + N-1 Comparisons done. So asymptotically it’s O(N).
Auxiliary Space: O(N)