Find minimum value of the expression by choosing K elements from given array
Last Updated :
15 Sep, 2022
Given an array of integers arr of size N, the task is to find the minimum possible of the expression by choosing exactly K(? N) integers form given array arr. Let say if chosen elements are stored in array B (B1, B2, B3…..Bk) then value of expression:
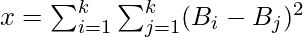
Examples:
Input : arr[] = {2, 0, 9, 5}, k = 2
Output : 8
Let say, chosen elements are {2, 0}, then x = 8, which is minimum possible
Input : arr[] = {4, 21, 5, 3, 8}, k = 3
Output : 200
Approach :
The above expression can be simplified as:
So, all we need to do is select the k smallest elements from the array and solve the expression.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumValue(int arr[], int n, int k)
{
sort(arr, arr + n);
int answer = 0;
for (int i = 0; i < k; i++)
answer += arr[i] * arr[i];
return answer * (2 * k - 2);
}
int main()
{
int arr[] = { 4, 21, 5, 3, 8 }, k = 3;
int n = sizeof(arr) / sizeof(arr[0]);
cout << minimumValue(arr, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int minimumValue(int arr[], int n, int k)
{
Arrays.sort(arr);
int answer = 0;
for (int i = 0; i < k; i++)
answer += arr[i] * arr[i];
return answer * (2 * k - 2);
}
public static void main(String[] args)
{
int arr[] = { 4, 21, 5, 3, 8 }, k = 3;
int n = arr.length;
System.out.print(minimumValue(arr, n, k));
}
}
|
Python3
def minimumValue(arr, n, k):
arr.sort();
answer = 0;
for i in range(k):
answer += arr[i] * arr[i];
return answer * (2 * k - 2);
if __name__ == '__main__':
arr = [ 4, 21, 5, 3, 8 ];
k = 3;
n = len(arr);
print(minimumValue(arr, n, k));
|
C#
using System;
class GFG{
static int minimumValue(int []arr, int n, int k)
{
Array.Sort(arr);
int answer = 0;
for (int i = 0; i < k; i++)
answer += arr[i] * arr[i];
return answer * (2 * k - 2);
}
public static void Main(String[] args)
{
int []arr = { 4, 21, 5, 3, 8 };
int k = 3;
int n = arr.Length;
Console.Write(minimumValue(arr, n, k));
}
}
|
Javascript
<script>
function minimumValue(arr, n, k)
{
arr.sort((a, b) => a - b);
let answer = 0;
for (let i = 0; i < k; i++)
answer += arr[i] * arr[i];
return answer * (2 * k - 2);
}
let arr = [ 4, 21, 5, 3, 8 ], k = 3;
let n = arr.length;
document.write(minimumValue(arr, n, k));
</script>
|
Time Complexity: O(n * log n)
Auxiliary Space: O(1)
Another Efficient Method: This problem can be solved efficiently using a Priority Queue. As we have to find the k smallest elements from the array in order to solve the expression so we use a priority queue which will find the k smallest elements in O(n*log(k)) time complexity where n is the size of the array and k is the number of smallest elements needed. Once we get the k smallest elements in the priority queue we will use the simplified expression given above to find the minimum value.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumValue(int arr[], int n, int k)
{
priority_queue<int> heap1;
for (int i = 0; i < n; ++i) {
heap1.push(arr[i]);
if (heap1.size() > k) {
heap1.pop();
}
}
int answer = 0;
for (int i = 0; i < k; i++)
{
answer += heap1.top() * heap1.top();
heap1.pop();
}
return answer * (2 * k - 2);
}
int main()
{
int arr[] = { 4, 21, 5, 3, 8 }, k = 3;
int n = sizeof(arr) / sizeof(arr[0]);
cout << minimumValue(arr, n, k);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int minimumValue(int[] arr, int n, int k)
{
PriorityQueue<Integer> heap1
= new PriorityQueue<Integer>(
Collections.reverseOrder());
for (int i = 0; i < n; ++i) {
heap1.add(arr[i]);
if (heap1.size() > k) {
heap1.poll();
}
}
int answer = 0;
for (var i = 0; i < k; i++) {
answer += heap1.peek() * heap1.peek();
heap1.poll();
}
return answer * (2 * k - 2);
}
public static void main(String[] args)
{
int[] arr = { 4, 21, 5, 3, 8 };
int k = 3;
int n = arr.length;
System.out.println(minimumValue(arr, n, k));
}
}
|
Python3
def minimumValue(arr, n, k):
heap1 = [];
for i in range(n):
heap1.append(arr[i]);
heap1.sort(reverse = True)
if (len(heap1) > k):
heap1.pop(0);
answer = 0;
for i in range(k):
answer += heap1[0] * heap1[0];
heap1.pop(0);
return answer * (2 * k - 2);
arr = [4, 21, 5, 3, 8 ]
k = 3;
n = len(arr);
print(minimumValue(arr, n, k));
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int minimumValue(int[] arr, int n, int k)
{
List<int> heap1 = new List<int>();
for (int i = 0; i < n; ++i) {
heap1.Add(arr[i]);
heap1.Sort();
heap1.Reverse();
if (heap1.Count > k) {
heap1.RemoveAt(0);
}
}
int answer = 0;
for (var i = 0; i < k; i++) {
answer += heap1[0] * heap1[0];
heap1.RemoveAt(0);
}
return answer * (2 * k - 2);
}
public static void Main(string[] args)
{
int[] arr = { 4, 21, 5, 3, 8 };
int k = 3;
int n = arr.Length;
Console.WriteLine(minimumValue(arr, n, k));
}
}
|
Javascript
function minimumValue(arr, n, k)
{
let heap1 = [];
for (var i = 0; i < n; ++i) {
heap1.push(arr[i]);
heap1.sort(function(a, b) { return a < b})
if (heap1.length > k) {
heap1.shift();
}
}
let answer = 0;
for (var i = 0; i < k; i++)
{
answer += heap1[0] * heap1[0];
heap1.shift();
}
return answer * (2 * k - 2);
}
let arr = [4, 21, 5, 3, 8 ]
let k = 3;
let n = arr.length;
console.log(minimumValue(arr, n, k));
|
Time Complexity: O(k+nlog(k)) where n is the size of the array and k is the given number of elements to choose from.
Auxiliary Space: O(k) since the priority queue at any time holds k elements.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...