Find minimum operations needed to make an Array beautiful
Last Updated :
08 Sep, 2022
Given a binary array( consider it as cyclic with start and end tied together) of length N having only one’s and zero’s where 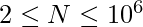 . The task is to find minimum operation needed to make the array beautiful.
. The task is to find minimum operation needed to make the array beautiful.
An array is said to be beautiful if it has no consecutive ones or zeros. If not possible then print -1.
In one operation, you can do the following:
- Cut the array in two parts.
- Reverse one of these two parts.
- Join the corresponding endpoints of these two parts, creating one whole array again.
Find the minimum number of above operations to be performed on the array to make it beautiful such that it does not contains any consecutive one’s or zero’s.
Examples:
Input : A[] = { 1, 1, 0, 0 }
Output : 1
Explanation:
Make first cut between A[0] and A[1]
and second cut between A[2] and A[3].
Reverse array A[1] to A[2] and tie both array together.
Thus new array is A = [1, 0, 1, 0] which is beautiful.
Input : A[] = { 1, 1, 0, 0, 0 }
Output : -1
Approach: The goal is to make the array either of the form A1[] = { 1, 0, 1, …, 0, 1, 0 } or A2[] = { 0, 1, 0, … 1, 0, 1 }.
- If we have odd number of elements then it is impossible to make array beautiful as we always one binary number extra than other. Hence we return -1.
- If we have even number of elements then we can make any of array A1 or A2 only when we have binary zeros and ones equal count.
- Also, the minimum cut required is the amount of consecutive zero or ones we have and will be equal.
- So, we iterate the array and maintain the count of zeros and ones and also consecutive zeros.
- If zero = one, then return count of consecutive zeros, else return -1.
Note: One special case is when there is only one element in the array. If there is only 1 element present in the array, then the array is already beautiful so the answer is zero.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minOperations(int A[], int n)
{
if (n & 1)
return -1;
int zeros = 0, consZeros = 0, ones = 0;
for (int i = 0; i < n; ++i) {
A[i] == 0 ? zeros++ : ones++;
if (i + 1 < n) {
if (A[i] == 0 && A[i + 1] == 0)
consZeros++;
}
}
if (A[0] == A[n - 1] && A[0] == 0)
consZeros++;
if (zeros == ones)
return consZeros;
else
return -1;
}
int main()
{
int A[] = { 1, 1, 0, 0 };
int n = sizeof(A) / sizeof(A[0]);
cout << minOperations(A, n);
return 0;
}
|
Java
class GFG{
static int minOperations(int[] A, int n)
{
if ((n & 1)>0)
return -1;
int zeros = 0, consZeros = 0, ones = 0;
for (int i = 0; i < n; ++i) {
if(A[i] == 0) zeros++; else ones++;
if (i + 1 < n) {
if (A[i] == 0 && A[i + 1] == 0)
consZeros++;
}
}
if (A[0] == A[n - 1] && A[0] == 0)
consZeros++;
if (zeros == ones)
return consZeros;
else
return -1;
}
public static void main(String[] args)
{
int[] A =new int[] { 1, 1, 0, 0 };
int n = A.length;
System.out.println(minOperations(A, n));
}
}
|
Python3
def minOperations(A, n) :
if n & 1 :
return -1
zeros, consZeros, ones = 0, 0, 0
for i in range(n) :
if A[i] :
zeros += 1
else :
ones += 1
if( i + 1 < n) :
if A[i] == 0 and A[i + 1] == 0 :
consZeros += 1
if A[0] == A[n - 1] and A[0] == 0 :
consZeros += 1
if zeros == ones :
return consZeros
else :
return -1
if __name__ == "__main__" :
A = [1, 1, 0, 0]
n = len(A)
print(minOperations(A, n))
|
C#
class GFG{
static int minOperations(int[] A, int n)
{
if ((n & 1)>0)
return -1;
int zeros = 0, consZeros = 0, ones = 0;
for (int i = 0; i < n; ++i) {
if(A[i] == 0) zeros++; else ones++;
if (i + 1 < n) {
if (A[i] == 0 && A[i + 1] == 0)
consZeros++;
}
}
if (A[0] == A[n - 1] && A[0] == 0)
consZeros++;
if (zeros == ones)
return consZeros;
else
return -1;
}
static void Main()
{
int[] A =new int[] { 1, 1, 0, 0 };
int n = A.Length;
System.Console.WriteLine(minOperations(A, n));
}
}
|
PHP
<?php
function minOperations($A, $n)
{
if ($n & 1)
return -1;
$zeros = 0;
$consZeros = 0;
$ones = 0;
for ($i = 0; $i < $n; ++$i)
{
$A[$i] == 0 ? $zeros++ : $ones++;
if (($i + 1) < $n)
{
if ($A[$i] == 0 &&
$A[$i + 1] == 0)
$consZeros++;
}
}
if ($A[0] == $A[$n - 1] &&
$A[0] == 0)
$consZeros++;
if ($zeros == $ones)
return $consZeros;
else
return -1;
}
$A = array( 1, 1, 0, 0 );
$n = sizeof($A);
echo minOperations($A, $n);
?>
|
Javascript
<script>
function minOperations(A, n)
{
if ((n & 1)>0)
return -1;
let zeros = 0, consZeros = 0, ones = 0;
for (let i = 0; i < n; ++i) {
if(A[i] == 0) zeros++; else ones++;
if (i + 1 < n) {
if (A[i] == 0 && A[i + 1] == 0)
consZeros++;
}
}
if (A[0] == A[n - 1] && A[0] == 0)
consZeros++;
if (zeros == ones)
return consZeros;
else
return -1;
}
let A = [ 1, 1, 0, 0 ];
let n = A.length;
document.write(minOperations(A, n));
</script>
|
Complexity Analysis:
- Time Complexity: O(N)
- Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...