Find minimum number of Log value needed to calculate Log upto N

Given an integer N. The task is to find the minimum number of log values needed to calculate all the log values from 1 to N using properties of the logarithm.
Examples: 

Input : N = 6
Output : 3
Value of log1 is already know, i.e. 0.
Except this the three log values needed are,
log2, log3, log5.

Input : N = 4
Output : 2

One of the properties of log function is: 

log(x.y) = log(x) + log(y)

Hence, to calculate log(x.y), we must know log values of x and y. Let us understand the concept using an example, for N = 6. Let ans denotes the number of log values needed to find all log values from 1 to 6. 

• log(1)=0 (implicit).
• To calculate log(2), we must know its value prior, we can’t find this using property.so, ans become 1.
• To calculate log(3), we must know its value prior, we can’t find this using property.so, ans become 2.
• To calculate log(4), we can use property, log(4)=log(2.2)=log(2)+log(2).As we already find log(2) hence ans remains 2.
• To calculate log(5), we must know its value prior, we can’t find this using property.so, ans become 3.
• To calculate log(6), we can use property, log(6)=log(2.3)=log(2)+log(3).As we already find log(2) and log(3), hence ans remains 3.

The idea is very simple, on observing carefully you will find that you can’t calculate log values of prime number as it has no divisor(other than 1 and itself). So, the task reduces to find all prime numbers from 1 to N.
Below is the implementation of the above approach: 

C++

// C++ program to find number of log values
// needed to calculate all the log values
// from 1 to N

#include <bits/stdc++.h>
using namespace std;

#define MAX 1000005

// In this vector prime[i] will store true
// if prime[i] is prime, else store false
vector<bool> prime(MAX, true);

// Using sieve of Eratosthenes to find
// all prime upto N
void sieve(int N)
{
    prime[0] = prime[1] = false;

    for (int i = 2; i <= N; i++) {
        if (prime[i]) {
            for (int j = 2; i * j <= N; j++)
                prime[i * j] = false;
        }
    }
}

// Function to find number of log values needed
// to calculate all the log values from 1 to N
int countLogNeeded(int N)
{
    int count = 0;

    // calculate primes upto N
    sieve(N);

    for (int i = 1; i <= N; i++) {
        if (prime[i])
            count++;
    }

    return count;
}

// Driver code
int main()
{
    int N = 6;

    cout<<countLogNeeded(N)<<endl;

    return 0;
}

Java

// Java program to find number of log values
// needed to calculate all the log values
// from 1 to N
import java.util.*;

class GFG
{

    static int MAX = 1000005;

    // In this vector prime[i] will store true
    // if prime[i] is prime, else store false
    static Vector<Boolean> prime = new Vector<>(MAX);

    static void vecIni()
    {
        for (int i = 0; i < MAX; i++)
        {
            prime.add(i, true);
        }
    }

    // Using sieve of Eratosthenes to find
    // all prime upto N
    static void sieve(int N)
    {
        prime.add(0, false);
        prime.add(1, false);

        for (int i = 2; i <= N; i++)
        {
            if (prime.get(i))
            {
                for (int j = 2; i * j <= N; j++)
                {
                    prime.add(i * j, false);
                }
            }
        }
    }

    // Function to find number of log values needed
    // to calculate all the log values from 1 to N
    static int countLogNeeded(int N)
    {
        int count = 0;

        // calculate primes upto N
        sieve(N);

        for (int i = 1; i <= N; i++)
        {
            if (prime.get(i))
            {
                count++;
            }
        }

        return count;
    }

    // Driver code
    public static void main(String[] args)
    {
        vecIni();
        int N = 6;
        System.out.println(countLogNeeded(N));
    }
}

/* This code contributed by PrinciRaj1992 */

Python3

# Python3 program to find number of log values
# needed to calculate all the log values
# from 1 to N

MAX = 1000005

# In this list prime[i] will store true
# if prime[i] is prime, else store false
prime = [True for i in range(MAX)]

# Using sieve of Eratosthenes to find
# all prime upto N
def sieve(N):

    prime[0], prime[1] = False, False

    for i in range(2, N + 1):
        if(prime[i]):
            for j in range(2, N + 1):
                if(i * j > N):
                    break
                prime[i * j] = False


# Function to find number of log values needed
# to calculate all the log values from 1 to N
def countLogNeeded(N):

    count = 0

    # calculate primes upto N
    sieve(N)

    for i in range(1, N + 1):
        if(prime[i]):
            count = count + 1

    return count

# Driver code
if __name__=='__main__':
    N = 6
    print(countLogNeeded(N))

# This code is contributed by
# Sanjit_Prasad

C#

// C# program to find number of log values
// needed to calculate all the log values
// from 1 to N
using System;
using System.Collections.Generic;
using System.Linq;

class GFG
{

    static int MAX = 1000005;

    // In this vector prime[i] will store true
    // if prime[i] is prime, else store false
    static List<Boolean> prime = new List<Boolean>(MAX);

    static void vecIni()
    {
        for (int i = 0; i < MAX; i++)
        {
            prime.Add(true);
        }
    }

    // Using sieve of Eratosthenes to find
    // all prime upto N
    static void sieve(int N)
    {
        prime.Insert(0, false);
        prime.Insert(1, false);

        for (int i = 2; i <= N; i++)
        {
            if (prime[i])
            {
                for (int j = 2; i * j <= N; j++)
                {
                    prime.Insert(i * j, false);
                }
            }
        }
    }

    // Function to find number of log values needed
    // to calculate all the log values from 1 to N
    static int countLogNeeded(int N)
    {
        int count = 0;

        // calculate primes upto N
        sieve(N);

        for (int i = 1; i <= N; i++)
        {
            if (prime[i])
            {
                count++;
            }
        }

        return count;
    }

    // Driver code
    public static void Main()
    {
        vecIni();
        int N = 6;
        Console.Write(countLogNeeded(N));
    }
}

/* This code contributed by Mohit kumar */

Javascript

<script>

// Javascript program to find number of log values
// needed to calculate all the log values
// from 1 to N

MAX = 1000005

// In this vector prime[i] will store true
// if prime[i] is prime, else store false
var prime = Array(MAX).fill(true);

// Using sieve of Eratosthenes to find
// all prime upto N
function sieve(N)
{
    prime[0] = prime[1] = false;

    for (var i = 2; i <= N; i++) {
        if (prime[i]) {
            for (var j = 2; i * j <= N; j++)
                prime[i * j] = false;
        }
    }
}

// Function to find number of log values needed
// to calculate all the log values from 1 to N
function countLogNeeded(N)
{
    var count = 0;

    // calculate primes upto N
    sieve(N);

    for (var i = 1; i <= N; i++) {
        if (prime[i])
            count++;
    }

    return count;
}

// Driver code
var N = 6;

document.write( countLogNeeded(N));

</script>

Output:

3

Time Complexity: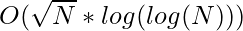
Auxiliary Space: O(N)