Find the minimum and maximum amount to buy all N candies
Last Updated :
15 Sep, 2023
In a candy store, there are N different types of candies available and the prices of all the N different types of candies are provided. There is also an attractive offer by the candy store. We can buy a single candy from the store and get at most K other candies (all are different types) for free.
- Find the minimum amount of money we have to spend to buy all the N different candies.
- Find the maximum amount of money we have to spend to buy all the N different candies.
In both cases, we must utilize the offer and get the maximum possible candies back. If k or more candies are available, we must take k candies for every candy purchase. If less than k candies are available, we must take all candies for a candy purchase.
Examples:
Input :
price[] = {3, 2, 1, 4}
k = 2
Output :
Min = 3, Max = 7
Explanation :
Since k is 2, if we buy one candy we can take
atmost two more for free.
So in the first case we buy the candy which
costs 1 and take candies worth 3 and 4 for
free, also you buy candy worth 2 as well.
So min cost = 1 + 2 = 3.
In the second case we buy the candy which
costs 4 and take candies worth 1 and 2 for
free, also We buy candy worth 3 as well.
So max cost = 3 + 4 = 7.
One important thing to note is, we must use the offer and get maximum candies back for every candy purchase. So if we want to minimize the money, we must buy candies at minimum cost and get candies of maximum costs for free. To maximize the money, we must do the reverse. Below is an algorithm based on this.
First Sort the price array.
For finding minimum amount :
Start purchasing candies from starting
and reduce k free candies from last with
every single purchase.
For finding maximum amount :
Start purchasing candies from the end
and reduce k free candies from starting
in every single purchase.
Below image is an illustration of the above approach:
Minimum amount :

Maximum amount :
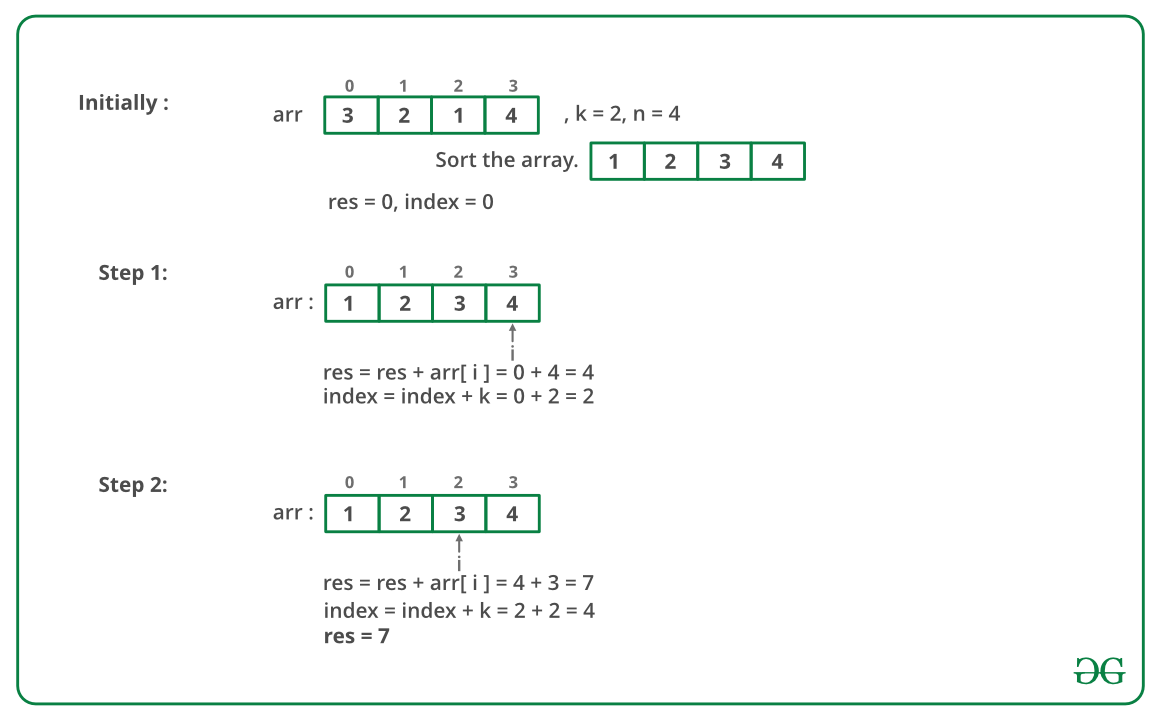
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findMinimum(int arr[], int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++) {
res += arr[i];
n = n - k;
}
return res;
}
int findMaximum(int arr[], int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
res += arr[i];
index += k;
}
return res;
}
int main()
{
int arr[] = { 3, 2, 1, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 2;
sort(arr, arr + n);
cout << findMinimum(arr, n, k) << " "
<< findMaximum(arr, n, k) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static int findMinimum(int arr[], int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++) {
res += arr[i];
n = n - k;
}
return res;
}
static int findMaximum(int arr[], int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
res += arr[i];
index += k;
}
return res;
}
public static void main(String[] args)
{
int arr[] = { 3, 2, 1, 4 };
int n = arr.length;
int k = 2;
Arrays.sort(arr);
System.out.println(findMinimum(arr, n, k) + " "
+ findMaximum(arr, n, k));
}
}
|
Python3
def findMinimum(arr, n, k):
res = 0
i = 0
while(i<n):
res += arr[i]
n = n-k
i += 1
return res
def findMaximum(arr, n, k):
res = 0
index = 0
i = n-1
while(i >= index):
res += arr[i]
index += k
i -= 1
return res
arr = [1,2,3,4,5,6,7,8,9,10]
n = len(arr)
k = 0
arr.sort()
print(findMinimum(arr, n, k), " ",
findMaximum(arr, n, k))
|
C#
using System;
public class GFG {
static int findMinimum(int[] arr, int n, int k)
{
int res = 0;
for (int i = 0; i < n; i++)
{
res += arr[i];
n = n - k;
}
return res;
}
static int findMaximum(int[] arr, int n, int k)
{
int res = 0, index = 0;
for (int i = n - 1; i >= index; i--)
{
res += arr[i];
index += k;
}
return res;
}
public static void Main()
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.Length;
int k = 2;
Array.Sort(arr);
Console.WriteLine(findMinimum(arr, n, k) + " "
+ findMaximum(arr, n, k));
}
}
|
PHP
<?php
function findMinimum($arr, $n,$k)
{
$res = 0;
for ($i = 0; $i < $n ; $i++)
{
$res += $arr[$i];
$n = $n - $k;
}
return $res;
}
function findMaximum($arr, $n, $k)
{
$res = 0;
$index = 0;
for ($i = $n - 1; $i >= $index; $i--)
{
$res += $arr[$i];
$index += $k;
}
return $res;
}
$arr = array(3, 2, 1, 4);
$n = sizeof($arr);
$k = 2;
sort($arr); sort($arr,$n);
echo findMinimum($arr, $n, $k)," "
,findMaximum($arr, $n, $k);
return 0;
?>
|
Javascript
<script>
function findMinimum(arr,n,k)
{
let res = 0;
for(let i = 0; i < n; i++)
{
res += arr[i];
n = n - k;
}
return res;
}
function findMaximum(arr,n,k)
{
let res = 0, index = 0;
for(let i = n - 1; i >= index; i--)
{
res += arr[i];
index += k;
}
return res;
}
let arr = [ 3, 2, 1, 4 ];
let n = arr.length;
let k = 2;
arr.sort(function(a, b){return a - b;});
document.write(findMinimum(arr, n, k) + " " +
findMaximum(arr, n, k));
</script>
|
Time Complexity : O(nlogn)
Auxiliary Space: O(1)
Another Implementation:
We can use the help of The Least integer function (Ceiling function) using built-in ceil() function to implement:
Below is the implementation in Python:
C++
#include <bits/stdc++.h>
using namespace std;
void find(vector<int> arr, int n, int k)
{
sort(arr.begin(), arr.end());
int b = ceil(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.size(); i++)
max_sum += arr[i];
cout << "minimum " << min_sum << endl;
cout << "maximum " << max_sum << endl;
}
int main()
{
vector<int> arr = {3, 2, 1, 4};
int n = arr.size();
int k = 2;
find(arr,n,k);
}
|
Java
import java.io.*;
import java.util.Arrays;
import java.lang.Math;
class GFG{
static void find(int[] arr, int n, int k)
{
Arrays.sort(arr);
int b = (int)Math.ceil(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.length; i++)
max_sum += arr[i];
System.out.println("minimum " + min_sum);
System.out.println("maximum " + max_sum);
}
public static void main (String[] args)
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.length;
int k = 2;
find(arr, n, k);
}
}
|
Python3
from math import ceil
def find(arr,n,k):
arr.sort()
b = int(ceil(n/k))
print("minimum ",sum(arr[:b]))
print("maximum ", sum(arr[-b:]))
arr = [3, 2, 1, 4]
n = len(arr)
k = 2
find(arr,n,k)
|
C#
using System;
class GFG{
static void find(int[] arr, int n, int k)
{
Array.Sort(arr);
int b = (int)Math.Ceiling(n / k * 1.0);
int min_sum = 0, max_sum = 0;
for(int i = 0; i < b; i++)
min_sum += arr[i];
for(int i = 2; i < arr.Length; i++)
max_sum += arr[i];
Console.WriteLine("minimum " + min_sum);
Console.WriteLine("maximum " + max_sum);
}
public static void Main()
{
int[] arr = { 3, 2, 1, 4 };
int n = arr.Length;
int k = 2;
find(arr, n, k);
}
}
|
Javascript
<script>
function find(arr,n,k)
{
arr.sort(function(a,b){return a-b;});
let b = Math.floor(Math.ceil(n/k));
let min_sum = 0, max_sum = 0;
for(let i = 0; i < b; i++)
min_sum += arr[i];
for(let i = 2; i < arr.length; i++)
max_sum += arr[i];
document.write("minimum "+min_sum+"<br>");
document.write("maximum "+ max_sum+"<br>");
}
let arr = [3, 2, 1, 4];
let n = arr.length;
let k = 2;
find(arr,n,k);
</script>
|
Output
('minimum ', 3)
('maximum ', 7)
Time Complexity: O(nlog(n))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...