Find maximum value of x such that n! % (k^x) = 0
Last Updated :
24 Mar, 2023
Given two integers 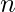 and
and 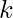 . The task is to find the maximum value of x, such that, n! % (k^x) = 0.
. The task is to find the maximum value of x, such that, n! % (k^x) = 0.
Examples:
Input : n = 5, k = 2
Output : 3
Explanation : Given n = 5 and k = 2. So, n! = 120.
Now for different values of x:
n! % 2^0 = 0,
n! % 2^1 = 0,
n! % 2^2 = 0,
n! % 2^3 = 0,
n! % 2^4 = 8,
n! % 2^5 = 24,
n! % 2^6 = 56,
n! % 2^7 = 120.
So, the answer should be 3.
Input : n = 1000, x = 2
Output : 994
Approach:
- First take the squareroot of
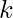 and store it in a variable say,
and store it in a variable say, 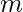 .
. - Run the loop from i=2 to m.
- If i = m then copy k to i.
- If k is divisible by i then divide k by i.
- Run a loop to n and add the quotient to a variable say,
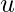 .
. - Store the minimum value of r after every loop.
Below is the implementation of the above approach:
C++
#include<iostream>
#include<math.h>
using namespace std;
class GfG
{
public:
int findX(int n, int k)
{
int r = n, v, u;
int m = sqrt(k) + 1;
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
r = min(r, u / v);
}
}
return r;
}
};
int main()
{
GfG g;
int n = 5;
int k = 2;
cout<<g.findX(n, k);
}
|
Java
import java.util.*;
public class GfG {
private static int findX(int n, int k)
{
int r = n, v, u;
int m = (int)Math.sqrt(k) + 1;
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
r = Math.min(r, u / v);
}
}
return r;
}
public static void main(String args[])
{
int n = 5;
int k = 2;
System.out.println(findX(n, k));
}
}
|
Python 3
import math
def findX(n, k):
r = n
m = int(math.sqrt(k)) + 1
i = 2
while i <= m and k > 1 :
if (i == m) :
i = k
u = 0
v = 0
while k % i == 0 :
k //= i
v += 1
if (v > 0) :
t = n
while (t > 0) :
t //= i
u += t
r = min(r, u // v)
i += 1
return r
if __name__ == "__main__":
n = 5
k = 2
print(findX(n, k))
|
C#
using System;
class GfG
{
public int findX(int n, int k)
{
int r = n, v, u;
int m = (int)Math.Sqrt(k) + 1;
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
r = Math.Min(r, u / v);
}
}
return r;
}
}
class geek
{
public static void Main()
{
GfG g = new GfG();
int n = 5;
int k = 2;
Console.WriteLine(g.findX(n, k));
}
}
|
PHP
<?php
function findX($n, $k)
{
$r = $n;
$m = (int)sqrt($k) + 1;
for ($i = 2; $i <= $m && $k > 1; $i++)
{
if ($i == $m)
{
$i = $k;
}
for ($u = $v = 0; $k % $i == 0; $v++)
{
$k = (int)($k / $i);
}
if ($v > 0)
{
$t = $n;
while ($t > 0)
{
$t = (int)($t / $i);
$u = $u + $t;
}
$r = min($r, (int)($u / $v));
}
}
return $r;
}
$n = 5;
$k = 2;
echo findX($n, $k);
?>
|
Javascript
<script>
function findX(n, k)
{
let r = n;
let v = 0;
let u = 0;
let m = Math.floor(Math.sqrt(k) + 1);
for (let i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
for (let u = v = 0; k % i == 0; v++) {
k = Math.floor(k / i);
}
if (v > 0) {
let t = n;
while (t > 0) {
t = Math.floor(t / i);
u += t;
}
r = Math.min(r, Math.floor(u / v));
}
}
return r;
}
let n = 5;
let k = 2;
document.write(findX(n, k));
</script>
|
Time complexity: O(sqrt(k)log(n)), where n is the input parameter n and k is the input parameter k.
Auxiliary space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...