Find maximum sum from top to bottom row with no adjacent diagonal elements
Last Updated :
29 Jun, 2022
Given a matrix A[][] of N * M, the task is to find the maximum sum from the top row to the bottom row after selecting one element from each row with no adjacent diagonal element.
Examples:
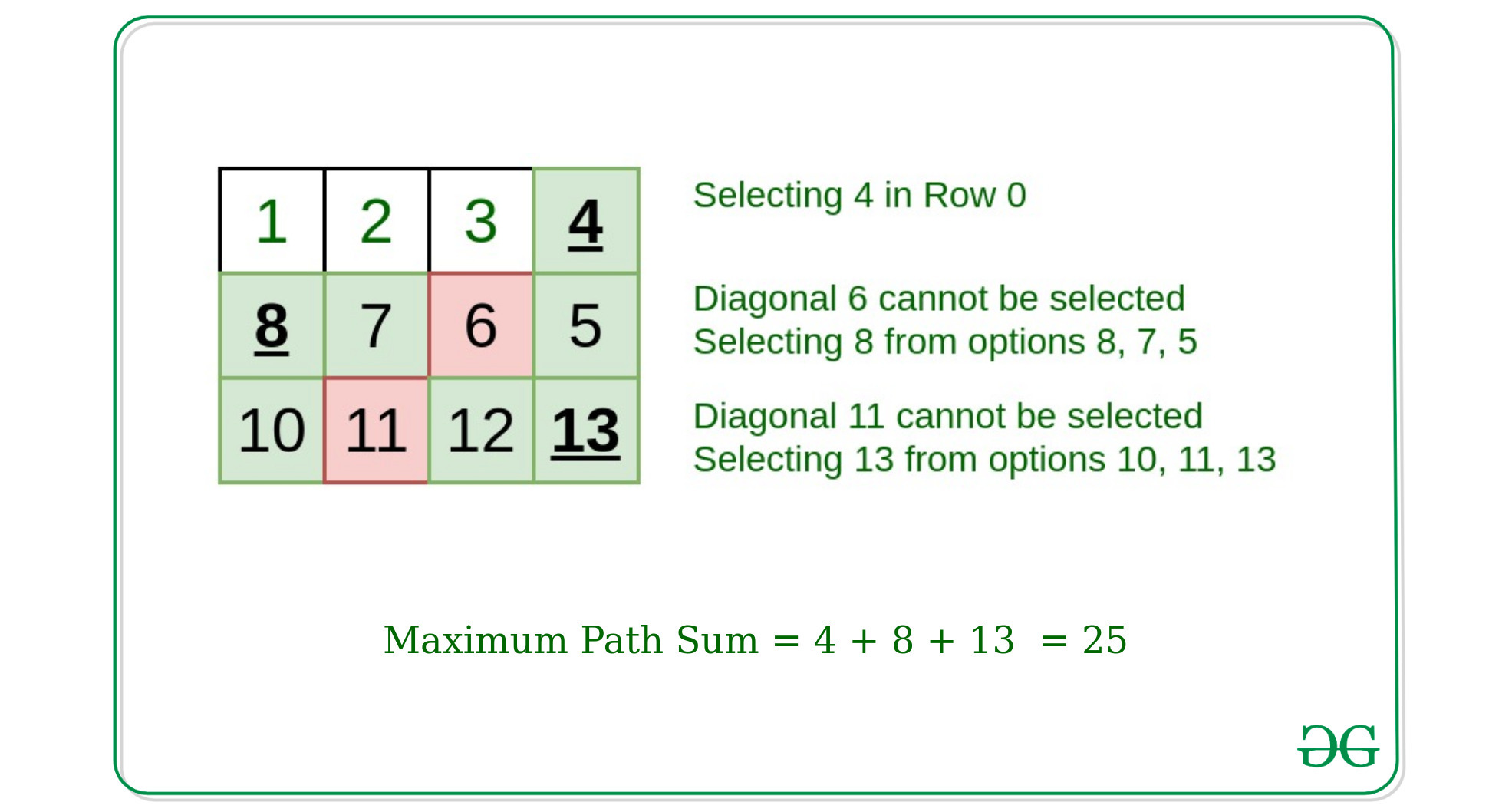
Input: A = { {1, 2, 3, 4}, {8, 7, 6, 5}, {10, 11, 12, 13} }
Output: 25
Explanation:
Selected elements to give maximum sum –
Row 0 = 4
Row 1 = 8
Row 2 = 13
Sum = 25
Input: A = { {1, 6}, {5, 3}, {11, 7} }
Output: 17
Explanation:
Selected elements to give maximum sum –
Row 0 = 1
Row 1 = 5
Row 2 = 11
Explanation: For Selecting any element if we have selected A[i][j], then elements A[i+1][j+1] and A[i+1][j-1] cannot be selected.
In the Given example Select the maximum element from the top-row where 4 is maximum in this case, then element A[1][2] cannot be selected which is 6, select the element 8 which maximum from the available options. Similarly, element 11 cannot be selected from the 3rd row. Select the element 13 to get the maximum sum which is 25.
Naive Approach: Generate all the combinations of N elements after choosing 1 element from every row and select the combination which produces maximum sum.
Efficient Approach: The idea is to use the concept of Dynamic programming in bottom up manner. Begin with the bottom most row of the given matrix and repeat the below process until we reach the top most row.
- Create an auxiliary array of the bottom most row elements with it corresponding indexes.
- Sort the auxiliary array.
- Iterate over the auxiliary array and for each element find maximum element from the row above to be added to the current element to produce maximum sum such that for every A[i][j] the selected element is not A[i-1][j+1] or A[i-1][j-1].
- Repeat this until reach to the topmost row of the given matrix array.
- Find the maximum element from the top row to get the maximum sum
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int maxSum(vector<vector<int> >& V,
int n, int m){
int ans = 0;
for (int i = n - 2; i >= 0; --i) {
vector<pair<int, int> > aux;
for (int j = 0; j < m; ++j) {
aux.push_back({ V[i + 1][j],
j });
}
sort(aux.begin(), aux.end());
reverse(aux.begin(), aux.end());
for (int j = 0; j < m; ++j) {
for (int k = 0; k < m; ++k) {
if (aux[k].second - j == 0 ||
abs(aux[k].second - j) > 1) {
V[i][j] += aux[k].first;
break;
}
}
}
}
for (int i = 0; i < m; ++i) {
ans = max(ans, V[0][i]);
}
return ans;
}
int main()
{
vector<vector<int> > V{{ 1, 2, 3, 4 },
{ 8, 7, 6, 5 },
{ 10, 11, 12, 13 }};
int n = V.size();
int m = V[0].size();
cout << maxSum(V, n, m);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG{
static int maxSum(int[][] V,
int n, int m)
{
int ans = 0;
for(int i = n - 2; i >= 0; --i)
{
ArrayList<int[]> aux = new ArrayList<>();
for(int j = 0; j < m; ++j)
{
aux.add(new int[]{V[i + 1][j], j});
}
Collections.sort(aux, (a, b) -> b[0] - a[0]);
for(int j = 0; j < m; ++j)
{
for(int k = 0; k < m; ++k)
{
if (aux.get(k)[1] - j == 0 ||
Math.abs(aux.get(k)[1] - j) > 1)
{
V[i][j] += aux.get(k)[0];
break;
}
}
}
}
for(int i = 0; i < m; ++i)
{
ans = Math.max(ans, V[0][i]);
}
return ans;
}
public static void main(String[] args)
{
int[][] V = { { 1, 2, 3, 4 },
{ 8, 7, 6, 5 },
{ 10, 11, 12, 13 } };
int n = V.length;
int m = V[0].length;
System.out.println(maxSum(V, n, m));
}
}
|
Python3
def maxSum(V, n, m):
ans = 0
for i in range(n - 2, -1, -1):
aux = []
for j in range(m):
aux.append([V[i + 1][j], j])
aux = sorted(aux)
aux = aux[::-1]
for j in range(m):
for k in range(m):
if (aux[k][1] - j == 0 or
abs(aux[k][1] - j) > 1):
V[i][j] += aux[k][0]
break
for i in range(m):
ans = max(ans, V[0][i])
return ans
if __name__ == '__main__':
V=[[ 1, 2, 3, 4 ],
[ 8, 7, 6, 5 ],
[ 10, 11, 12, 13]]
n = len(V)
m = len(V[0])
print(maxSum(V, n, m))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int maxSum(int[,] V, int n, int m){
int ans = 0;
for (int i = n - 2; i >= 0; --i) {
List<Tuple<int,int>> aux = new List<Tuple<int,int>>();
for (int j = 0; j < m; ++j) {
aux.Add(new Tuple<int,int>(V[i + 1, j], j));
}
aux.Sort();
aux.Reverse();
for (int j = 0; j < m; ++j) {
for (int k = 0; k < m; ++k) {
if (aux[k].Item2 - j == 0 ||
Math.Abs(aux[k].Item2 - j) > 1) {
V[i, j] += aux[k].Item1;
break;
}
}
}
}
for (int i = 0; i < m; ++i) {
ans = Math.Max(ans, V[0,i]);
}
return ans;
}
static void Main()
{
int[,] V = {{ 1, 2, 3, 4 },
{ 8, 7, 6, 5 },
{ 10, 11, 12, 13 }};
int n = V.GetLength(0);
int m = V.GetLength(1);
Console.WriteLine(maxSum(V, n, m));
}
}
|
Javascript
<script>
function maxSum(V, n, m){
let ans = 0;
for (let i = n - 2; i >= 0; --i) {
let aux = new Array();
for (let j = 0; j < m; ++j) {
aux.push([ V[i + 1][j], j ]);
}
aux.sort((a, b) => a[0] - b[0]);
aux.reverse();
for (let j = 0; j < m; ++j) {
for (let k = 0; k < m; ++k) {
if (aux[k][1] - j == 0 ||
Math.abs(aux[k][1] - j) > 1) {
V[i][j] += aux[k][0];
break;
}
}
}
}
for (let i = 0; i < m; ++i) {
ans = Math.max(ans, V[0][i]);
}
return ans;
}
let V = [[ 1, 2, 3, 4 ],
[ 8, 7, 6, 5 ],
[ 10, 11, 12, 13 ]];
let n = V.length;
let m = V[0].length;
document.write(maxSum(V, n, m));
</script>
|
Time Complexity: O(n*m2)
Auxiliary Space: O(m)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...