Find maximum count of duplicate nodes in a Binary Search Tree
Last Updated :
16 Aug, 2021
Given a Binary Search Tree (BST) with duplicates, find the node (the most frequently occurred element) in the given BST. If the BST contains two or more such nodes, print any of them.
Note: We cannot use any extra space. (Assume that the implicit stack space incurred due to recursion does not count)
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
- Both the left and right subtrees must also be binary search trees.
Examples:
Input : Given BST is
6
/ \
5 7
/ \ / \
4 5 7 7
Output : 7
Input : Given BST is
10
/ \
5 12
/ \ / \
5 6 12 16
Output : 5 or 12
We can print any of the two value 5 or 12.
Approach:
To find the node, we need to find the Inorder Traversal of the BST because its Inorder Traversal will be in sorted order.
So, the idea is to do recursive Inorder traversal and keeping the track of the previous node. If the current node value is equal to the previous value we can increase the current count and if the current count becomes greater than the maximum count, replace the element.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
struct Node {
int val;
struct Node *left, *right;
};
struct Node* newNode(int data)
{
struct Node* temp = new Node;
temp->val = data;
temp->left = temp->right = NULL;
return temp;
}
int cur = 1, mx = 0;
int node;
struct Node* previous = NULL;
void inorder(struct Node* root)
{
if (root == NULL) {
return;
}
inorder(root->left);
if (previous != NULL) {
if (root->val == previous->val) {
cur++;
}
else {
cur = 1;
}
}
if (cur > mx) {
mx = cur;
node = root->val;
}
previous = root;
inorder(root->right);
}
int findnode(struct Node* root)
{
inorder(root);
return node;
}
int main()
{
struct Node* root = newNode(6);
root->left = newNode(5);
root->right = newNode(7);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(7);
root->right->right = newNode(7);
cout << "Node of BST is " << findnode(root) << '\n';
return 0;
}
|
Java
class GFG
{
static class Node
{
int val;
Node left, right;
};
static Node newNode(int data)
{
Node temp = new Node();
temp.val = data;
temp.left = temp.right = null;
return temp;
}
static int cur = 1, mx = 0;
static int node;
static Node previous = null;
static void inorder(Node root)
{
if (root == null)
{
return;
}
inorder(root.left);
if (previous != null)
{
if (root.val == previous.val)
{
cur++;
}
else
{
cur = 1;
}
}
if (cur > mx)
{
mx = cur;
node = root.val;
}
previous = root;
inorder(root.right);
}
static int findnode(Node root)
{
inorder(root);
return node;
}
public static void main(String args[])
{
Node root = newNode(6);
root.left = newNode(5);
root.right = newNode(7);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(7);
root.right.right = newNode(7);
System.out.println("Node of BST is " +
findnode(root));
}
}
|
Python3
class Node:
def __init__(self):
self.val = 0
self.left = None
self.right = None
def newNode(data: int) -> Node:
temp = Node()
temp.val = data
temp.left = temp.right = None
return temp
cur = 1
mx = 0
node = 0
previous = Node()
def inorder(root: Node):
global cur, mx, node, previous
if root is None:
return
inorder(root.left)
if previous is not None:
if root.val == previous.val:
cur += 1
else:
cur = 1
if cur > mx:
mx = cur
node = root.val
previous = root
inorder(root.right)
def findNode(root: Node) -> int:
global node
inorder(root)
return node
if __name__ == "__main__":
root = newNode(6)
root.left = newNode(5)
root.right = newNode(7)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(7)
root.right.right = newNode(7)
print("Node of BST is", findNode(root))
|
C#
using System;
class GFG
{
public class Node
{
public int val;
public Node left, right;
};
static Node newNode(int data)
{
Node temp = new Node();
temp.val = data;
temp.left = temp.right = null;
return temp;
}
static int cur = 1, mx = 0;
static int node;
static Node previous = null;
static void inorder(Node root)
{
if (root == null)
{
return;
}
inorder(root.left);
if (previous != null)
{
if (root.val == previous.val)
{
cur++;
}
else
{
cur = 1;
}
}
if (cur > mx)
{
mx = cur;
node = root.val;
}
previous = root;
inorder(root.right);
}
static int findnode(Node root)
{
inorder(root);
return node;
}
public static void Main(String []args)
{
Node root = newNode(6);
root.left = newNode(5);
root.right = newNode(7);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(7);
root.right.right = newNode(7);
Console.WriteLine("Node of BST is " +
findnode(root));
}
}
|
Javascript
<script>
class Node
{
constructor()
{
this.val = 0;
this.left = null;
this.right = null;
}
};
function newNode(data)
{
var temp = new Node();
temp.val = data;
temp.left = temp.right = null;
return temp;
}
var cur = 1, mx = 0;
var node;
var previous = null;
function inorder(root)
{
if (root == null)
{
return;
}
inorder(root.left);
if (previous != null)
{
if (root.val == previous.val)
{
cur++;
}
else
{
cur = 1;
}
}
if (cur > mx)
{
mx = cur;
node = root.val;
}
previous = root;
inorder(root.right);
}
function findnode(root)
{
inorder(root);
return node;
}
var root = newNode(6);
root.left = newNode(5);
root.right = newNode(7);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(7);
root.right.right = newNode(7);
document.write("Node of BST is " +
findnode(root));
</script>
|
Time complexity : 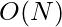
Auxiliary Space: O(N).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...