Find the last digit of given series

Difficulty Level : Easy
Last Updated : 09 Jan, 2019

Given an integer n, find the last digit of this sequence,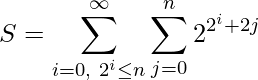 $\displaystyle S =\sum_{i=0,\ 2^i\le n}^\infty \sum_{j=0}^n 2^{2^i + 2j}$
i.e. Summation of F(n) from i = 0 to 2ⁱ ≤ n, where F(n) is the summation of 2^2ⁱ+2j Where j varies from 0 to n. n can varies from 0 to 10¹⁷
Examples:

Input: 2
Output: 6
Explanation:
After computing the above expression, the value
obtained is 216. Hence the last digit is 6.

Input: 3
Output: 0

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

A Naive approach is to run two loops, one for ‘i’ and other for ‘j’ and compute the value after taking (modulo 10) with every calculated value. But this approach will definitely time out for large value of n.

An efficient approach is to expand the above expression in a general form that can easily be calculated.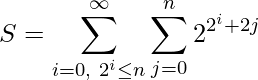

$\displaystyle S =\sum_{i=0,\ 2^i\le n}^\infty \sum_{j=0}^n 2^{2^i + 2j}$

$\implies \displaystyle \sum_{i=0,\ 2^i\le n}^\infty \sum_{j=0}^n 2^{2^i}\cdot 2^{2j}$

$\implies\displaystyle\sum_{i=0,\ 2^i\le n}^\infty 2^{2^i} \cdot \sum_{j=0}^n 2^{2j}$

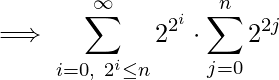$\implies\displaystyle\sum_{i=0,\ 2^i\le n}^\infty 2^{2^i} \cdot \sum_{j=0}^n 4^j$

First expression 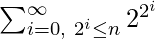$\sum_{i=0,\ 2^i\le n}^\infty 2^{2^i}$ can be calculated directly by iterating a loop for all values of ‘i’ till 2ⁱ ≤ n.
Second expression 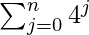$\sum_{j=0}^n 4^j$ can be calculated easily by using Geometric series formula i.e.,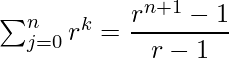
$\sum_{j=0}^n r^k = \dfrac{r^{n+1} - 1}{r-1}$

Final answer will be the product of both these calculated result in both the steps. But after performing any calculation part of these expression, we have to take modulo with 10 to avoid overflow.

See below programs to understand more.

C++

// C++ program to calculate to find last
// digit of above expression
#include <bits/stdc++.h>
using namespace std;
  
/* Iterative Function to calculate (x^y)%p in O(log y) */
long long powermod(long long x, long long y, long long p)
{
    long long res = 1; // Initialise result
  
    x = x % p; // Update x if it is more than or
              // equal to p
  
    while (y > 0) {
  
        // If y is odd, multiply x with result
        if (y & 1LL)
            res = (res * x) % p;
  
        // y must be even now
        y = y >> 1LL; // y = y/2
        x = (x * x) % p;
    }
    return res;
}
  
// Returns modulo inverse of a with respect to m 
// using extended Euclid Algorithm
long long modInverse(long long a, long long m)
{
    long long m0 = m, t, q;
    long long x0 = 0, x1 = 1;
  
    if (m == 1)
        return 0;
  
    while (a > 1) {
  
        // q is quotient
        q = a / m;
  
        t = m;
  
        // m is remainder now, process same as
        // Euclid's algo
        m = a % m, a = t;
  
        t = x0;
  
        x0 = x1 - q * x0;
  
        x1 = t;
    }
  
    // Make x1 positive
    if (x1 < 0)
        x1 += m0;
  
    return x1;
}
  
// Function to calculate the above expression
long long evaluteExpression(long long& n)
{
    // Initialize the result
    long long firstsum = 0, mod = 10;
  
    // Compute first part of expression
    for (long long i = 2, j = 0; (1LL << j) <= n; i *= i, ++j)
        firstsum = (firstsum + i) % mod;
  
    // Compute second part of expression
    // i.e., ((4^(n+1) - 1) / 3) mod 10
    // Since division of 3 in modulo can't
    // be performed directly therefore we
    // need to find it's modulo Inverse
    long long secondsum = (powermod(4LL, n + 1, mod) - 1) * 
                           modInverse(3LL, mod);
  
    return (firstsum * secondsum) % mod;
}
  
// Driver code
int main()
{
    long long n = 3;
    cout << evaluteExpression(n) << endl;
  
    n = 10;
    cout << evaluteExpression(n);
  
    return 0;
}

Java

// Java program to calculate to find last 
// digit of above expression 
  
class GFG{
/* Iterative Function to calculate (x^y)%p in O(log y) */
static long powermod(long x, long y, long p) 
{ 
    long res = 1; // Initialise result 
  
    x = x % p; // Update x if it is more than or 
            // equal to p 
  
    while (y > 0) { 
  
        // If y is odd, multiply x with result 
        if ((y & 1L)>0) 
            res = (res * x) % p; 
  
        // y must be even now 
        y = y >> 1L; // y = y/2 
        x = (x * x) % p; 
    } 
    return res; 
} 
  
// Returns modulo inverse of a with respect to m 
// using extended Euclid Algorithm 
static long modInverse(long a, long m) 
{ 
    long  m0 = m, t, q; 
    long  x0 = 0, x1 = 1; 
  
    if (m == 1) 
        return 0; 
  
    while (a > 1) { 
  
        // q is quotient 
        q = a / m; 
  
        t = m; 
  
        // m is remainder now, process same as 
        // Euclid's algo 
        m = a % m;
        a = t; 
  
        t = x0; 
  
        x0 = x1 - q * x0; 
  
        x1 = t; 
    } 
  
    // Make x1 positive 
    if (x1 < 0) 
        x1 += m0; 
  
    return x1; 
} 
  
// Function to calculate the above expression 
static long evaluteExpression(long n) 
{ 
    // Initialize the result 
    long firstsum = 0, mod = 10; 
  
    // Compute first part of expression 
    for (long i = 2, j = 0; (1L << j) <= n; i *= i, ++j) 
        firstsum = (firstsum + i) % mod; 
  
    // Compute second part of expression 
    // i.e., ((4^(n+1) - 1) / 3) mod 10 
    // Since division of 3 in modulo can't 
    // be performed directly therefore we 
    // need to find it's modulo Inverse 
    long secondsum = (powermod(4L, n + 1, mod) - 1) * 
                        modInverse(3L, mod); 
  
    return (firstsum * secondsum) % mod; 
} 
  
// Driver code 
public static void main(String[] args) 
{ 
    long n = 3; 
    System.out.println(evaluteExpression(n)); 
  
    n = 10; 
    System.out.println(evaluteExpression(n)); 
  
} 
}
// This code is contributed by mits

Python3

# Python3 program to calculate to find last 
# digit of above expression 
  
# Iterative Function to calculate (x^y)%p in O(log y) 
def powermod(x, y, p): 
   
    res = 1; # Initialise result 
  
    x = x % p; # Update x if it is more than or 
            # equal to p 
  
    while (y > 0):
  
        # If y is odd, multiply x with result 
        if ((y & 1)>0): 
            res = (res * x) % p; 
  
        # y must be even now 
        y = y >> 1; # y = y/2 
        x = (x * x) % p;
          
    return res; 
  
# Returns modulo inverse of a with respect to m 
# using extended Euclid Algorithm 
def modInverse(a, m):
   
    m0 = m; 
    x0 = 0;
    x1 = 1; 
  
    if (m == 1): 
        return 0; 
  
    while (a > 1): 
  
        # q is quotient 
        q = int(a / m); 
  
        t = m; 
  
        # m is remainder now, process same as 
        # Euclid's algo 
        m = a % m;
        a = t; 
  
        t = x0; 
  
        x0 = x1 - q * x0; 
  
        x1 = t; 
  
    # Make x1 positive 
    if (x1 < 0): 
        x1 += m0; 
  
    return x1; 
  
# Function to calculate the above expression 
def evaluteExpression(n): 
   
    # Initialize the result 
    firstsum = 0;
    mod = 10; 
  
    # Compute first part of expression
    i=2;
    j=0;
    while ((1 << j) <= n): 
        firstsum = (firstsum + i) % mod;
        i *= i;
        j+=1;
  
    # Compute second part of expression 
    # i.e., ((4^(n+1) - 1) / 3) mod 10 
    # Since division of 3 in modulo can't 
    # be performed directly therefore we 
    # need to find it's modulo Inverse 
    secondsum = (powermod(4, n + 1, mod) - 1) * modInverse(3, mod); 
  
    return (firstsum * secondsum) % mod; 
  
# Driver code 
  
n = 3; 
print(evaluteExpression(n)); 
  
n = 10; 
print(evaluteExpression(n)); 
  
# This code is contributed by mits

C#

// C# program to calculate to find last 
// digit of above expression 
  
class GFG{
/* Iterative Function to calculate (x^y)%p in O(log y) */
static long powermod(long x, long y, long p) 
{ 
    long res = 1; // Initialise result 
  
    x = x % p; // Update x if it is more than or 
            // equal to p 
  
    while (y > 0) { 
  
        // If y is odd, multiply x with result 
        if ((y & 1)>0) 
            res = (res * x) % p; 
  
        // y must be even now 
        y = y >> 1; // y = y/2 
        x = (x * x) % p; 
    } 
    return res; 
} 
  
// Returns modulo inverse of a with respect to m 
// using extended Euclid Algorithm 
static long modInverse(long a, long m) 
{ 
    long  m0 = m, t, q; 
    long  x0 = 0, x1 = 1; 
  
    if (m == 1) 
        return 0; 
  
    while (a > 1) { 
  
        // q is quotient 
        q = a / m; 
  
        t = m; 
  
        // m is remainder now, process same as 
        // Euclid's algo 
        m = a % m;
        a = t; 
  
        t = x0; 
  
        x0 = x1 - q * x0; 
  
        x1 = t; 
    } 
  
    // Make x1 positive 
    if (x1 < 0) 
        x1 += m0; 
  
    return x1; 
} 
  
// Function to calculate the above expression 
static long evaluteExpression(long n) 
{ 
    // Initialize the result 
    long firstsum = 0, mod = 10; 
  
    // Compute first part of expression 
    for (int i = 2, j = 0; (1 << j) <= n; i *= i, ++j) 
        firstsum = (firstsum + i) % mod; 
  
    // Compute second part of expression 
    // i.e., ((4^(n+1) - 1) / 3) mod 10 
    // Since division of 3 in modulo can't 
    // be performed directly therefore we 
    // need to find it's modulo Inverse 
    long secondsum = (powermod(4L, n + 1, mod) - 1) * 
                        modInverse(3L, mod); 
  
    return (firstsum * secondsum) % mod; 
} 
  
// Driver code 
public static void Main() 
{ 
    long n = 3; 
    System.Console.WriteLine(evaluteExpression(n)); 
  
    n = 10; 
    System.Console.WriteLine(evaluteExpression(n)); 
  
} 
}
// This code is contributed by mits

PHP

<?php
// PHP program to calculate to find 
// last digit of above expression 
  
/* Iterative Function to calculate
   (x^y)%p in O(log y) */
function powermod($x, $y, $p) 
{ 
    $res = 1; // Initialise result 
  
    $x = $x % $p; // Update x if it is more 
                  // than or equal to p 
  
    while ($y > 0)
    { 
  
        // If y is odd, multiply 
        // x with result 
        if (($y & 1) > 0) 
            $res = ($res * $x) % $p; 
  
        // y must be even now 
        $y = $y >> 1; // y = y/2 
        $x = ($x * $x) % $p; 
    } 
    return $res; 
} 
  
// Returns modulo inverse of a 
// with respect to m using 
// extended Euclid Algorithm 
function modInverse($a, $m) 
{ 
    $m0 = $m; 
    $x0 = 0;
    $x1 = 1; 
  
    if ($m == 1) 
        return 0; 
  
    while ($a > 1) 
    { 
  
        // q is quotient 
        $q = (int)($a / $m); 
  
        $t = $m; 
  
        // m is remainder now, process 
        // same as Euclid's algo 
        $m = $a % $m;
        $a = $t; 
  
        $t = $x0; 
  
        $x0 = $x1 - $q * $x0; 
  
        $x1 = $t; 
    } 
  
    // Make x1 positive 
    if ($x1 < 0) 
        $x1 += $m0; 
  
    return $x1; 
} 
  
// Function to calculate the
// above expression 
function evaluteExpression($n) 
{ 
    // Initialize the result 
    $firstsum = 0;
    $mod = 10; 
  
    // Compute first part of expression 
    for ($i = 2, $j = 0; (1 << $j) <= $n;
                          $i *= $i, ++$j) 
        $firstsum = ($firstsum + $i) % $mod; 
  
    // Compute second part of expression 
    // i.e., ((4^(n+1) - 1) / 3) mod 10 
    // Since division of 3 in modulo can't 
    // be performed directly therefore we 
    // need to find it's modulo Inverse 
    $secondsum = (powermod(4, $n + 1, $mod) - 1) * 
                  modInverse(3, $mod); 
  
    return ($firstsum * $secondsum) % $mod; 
} 
  
// Driver code 
$n = 3; 
echo evaluteExpression($n) . "\n"; 
  
$n = 10; 
echo evaluteExpression($n); 
  
// This code is contributed by mits
?>

Output:

0
8

Time complexity: O(log(n))
Auxiliary space: O(1)

Note: Asked in TCS Code vita contest.

This article is contributed by Shubham Bansal. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

C++

Java

Python3

C#

PHP