Find Kth lexicographical ordered numeric string of length N with distinct products of each substring
Last Updated :
04 Aug, 2022
Given two integers N and K, the task is to find the Kth lexicographical ordered string of length N, which has distinct products of each of the substrings, return -1 if such a string does not exist.
Example:
Input: N = 3, K = 4
Output: 238
Explanation: The valid strings series is “234”, “235”, “237”, “238”. The 4th string in the series is “238” and the product of all its substrings {2, 3, 8, 6, 24, 48} is distinct.
Input: N = 1, K = 11
Output: -1
Explanation: There are only 10 valid strings of length 1: “0”, “1”, “2”, “3”, “4”, “5”, “6”, “7”, “8”, “9”.
Approach: The problem can be solved using recursion. Recursively check all possible numeric strings of length N and find Kth valid numeric string with distinct products of each substring.
Follow the steps to solve the problem:
- Notice when any two characters repeat in the string, it will not be a valid string as two substrings of length 1 will same product.
- All strings with length N > 10 will have no answer because at least one character will be repeated.
- For strings of length > 1, strings that will have ‘1’ or ‘0’ in them will not be valid as any number multiplied with these characters will be the same or converted to 0.
- Maintain a recursive function to calculate the total possible strings with the character ‘0’ -> ‘1’.
- Keep track of all the products till now and if the product is repeated then exit the function immediately.
- Start from 0->9 one by one and if a valid string is obtained then decrease K. For, any string S if K becomes 0, this string will be the final answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void getString(int curlen, string& ans,
string& s, int N,
int& K, vector<int>& prod)
{
if (curlen == N) {
K--;
if (K == 0)
ans = s;
return;
}
char ch;
int ok, t, i;
for (ch = '2'; ch <= '9'; ch++) {
s += ch;
ok = 1;
t = 1;
for (i = curlen; i >= 0; i--) {
t *= s[i] - 48;
if (prod[t])
ok = 0;
prod[t]++;
}
if (ok)
getString(curlen + 1, ans,
s, N, K, prod);
t = 1;
for (i = curlen; i >= 0; i--) {
t *= s[i] - 48;
prod[t]--;
}
s.erase(s.length() - 1);
}
}
string kthValidString(int N, int K)
{
if (N > 10) {
return "-1";
}
if (N == 1) {
if (K > 10) {
return "-1";
}
string s = "";
K--;
s += (K + '0');
return s;
}
string ans = "-1";
string s = "";
vector<int> prod(10005, 0);
getString(0, ans, s, N, K, prod);
return ans;
}
int main()
{
int N = 3, K = 4;
cout << kthValidString(N, K);
}
|
Java
import java.util.*;
class GFG{
static String ans,s;
static int K;
static void getString(int curlen, int N, int[] prod)
{
if (curlen == N) {
K--;
if (K == 0)
ans = s;
return;
}
char ch;
int ok, t, i;
for (ch = '2'; ch <= '9'; ch++) {
s += ch;
ok = 1;
t = 1;
for (i = curlen ; i >= 0 && s.length()>i; i--) {
t *= s.charAt(i) - 48;
if (prod[t]!=0)
ok = 0;
prod[t]++;
}
if (ok!=0)
getString(curlen + 1, N, prod);
t = 1;
for (i = curlen; i >= 0&& s.length()>i; i--) {
t *= s.charAt(i) - 48;
prod[t]--;
}
if(s.length()>0)
s=s.substring(0,s.length() - 1);
}
}
static String kthValidString(int N)
{
if (N > 10) {
return "-1";
}
if (N == 1) {
if (K > 10) {
return "-1";
}
String s = "";
K--;
s += (K + '0');
return s;
}
ans = "-1";
s = "";
int []prod = new int[10005];
getString(0, N, prod);
return ans;
}
public static void main(String[] args)
{
int N = 3;
K = 4;
System.out.print(kthValidString(N));
}
}
|
C#
using System;
class GFG{
static String ans,s;
static int K;
static void getString(int curlen, int N, int[] prod)
{
if (curlen == N)
{
K--;
if (K == 0)
ans = s;
return;
}
char ch;
int ok, t, i;
for(ch = '2'; ch <= '9'; ch++)
{
s += ch;
ok = 1;
t = 1;
for(i = curlen ; i >= 0 && s.Length>i; i--)
{
t *= s[i] - 48;
if (prod[t] != 0)
ok = 0;
prod[t]++;
}
if (ok != 0)
getString(curlen + 1, N, prod);
t = 1;
for(i = curlen; i >= 0 && s.Length>i; i--)
{
t *= s[i] - 48;
prod[t]--;
}
if (s.Length > 0)
s = s.Substring(0,s.Length - 1);
}
}
static String kthValidString(int N)
{
String s = "";
if (N > 10)
{
return "-1";
}
if (N == 1)
{
if (K > 10)
{
return "-1";
}
s = "";
K--;
s += (K + '0');
return s;
}
ans = "-1";
s = "";
int []prod = new int[10005];
getString(0, N, prod);
return ans;
}
public static void Main(String[] args)
{
int N = 3;
K = 4;
Console.Write(kthValidString(N));
}
}
|
Python3
s = ''
K = 0
def getString(curlen, N, prod):
global s, K
if (curlen == N):
K -= 1
if (K == 0):
ans = s
return
ch = '2'
while(ch <= '9'):
s = chr(ord(s)+ ord(ch))
ok = 1
t = 1
i = curlen
ch = chr(ord(ch) + 1)
while(i >= 0 and len(s)) :
t *= ord(s[i]) - 48
if (prod[t] != 0):
ok = 0
prod[t] += 1
i -= 1
if (ok != 0):
getString(curlen + 1, N, prod)
t = 1
i = curlen
while(i >= 0 and len(s)>i):
i-=1
t *= ord(s[i]) - 48
prod[t] -= 1
if(len(s)>0):
s = s[0: len(s) - 1]
def kthValidString(N):
if (N > 10):
return "-1"
if (N == 1):
if (K > 10):
return "-1"
s = ""
K-=1
s += (K + '0')
return s
ans = "-1"
s = ""
prod = [0]*10005
getString(0, N, prod)
return ans
N = 3
K = 4
print(kthValidString(N))
|
Javascript
<script>
var ans,s;
var K;
function getString(curlen, N, prod)
{
if (curlen == N) {
K--;
if (K == 0)
ans = s;
return;
}
var ch;
var ok, t, i;
for (ch = '2'; ch <= '9'; ch++) {
s += ch;
ok = 1;
t = 1;
for (i = curlen ; i >= 0 && s.length > i; i--) {
t *= s.charAt(i) - 48;
if (prod[t] != 0)
ok = 0;
prod[t]++;
}
if (ok!=0)
getString(curlen + 1, N, prod);
t = 1;
for (i = curlen; i >= 0&& s.length > i; i--) {
t *= s.charAt(i) - 48;
prod[t]--;
}
if(s.length>0)
s = s.substring(0,s.length - 1);
}
}
function kthValidString(N)
{
if (N > 10) {
return "-1";
}
if (N == 1)
{
if (K > 10) {
return "-1";
}
var s = "";
K--;
s += (K + '0');
return s;
}
var ans = "1";
var s = "";
var prod = new Array(10005);
getString(0, N, prod);
return ans;
}
var N = 3;
var K = 4;
document.write(kthValidString(N));
</script>
|
Time Complexity: 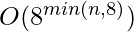
Auxiliary Space: 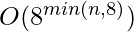
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...