Find k-th smallest element in BST (Order Statistics in BST)
Last Updated :
11 Oct, 2023
Given the root of a binary search tree and K as input, find Kth smallest element in BST.
For example, in the following BST, if k = 3, then the output should be 10, and if k = 5, then the output should be 14.
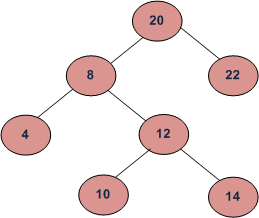
Method 1: Using Inorder Traversal (O(n) time and O(h) auxiliary space)
The Inorder Traversal of a BST traverses the nodes in increasing order. So the idea is to traverse the tree in Inorder. While traversing, keep track of the count of the nodes visited. If the count becomes k, print the node.
C++
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
Node(int x)
{
data = x;
left = right = NULL;
}
};
Node* insert(Node* root, int x)
{
if (root == NULL)
return new Node(x);
if (x < root->data)
root->left = insert(root->left, x);
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
int count = 0;
Node* kthSmallest(Node* root, int& k)
{
if (root == NULL)
return NULL;
Node* left = kthSmallest(root->left, k);
if (left != NULL)
return left;
count++;
if (count == k)
return root;
return kthSmallest(root->right, k);
}
void printKthSmallest(Node* root, int k)
{
Node* res = kthSmallest(root, k);
if (res == NULL)
cout << "There are less than k nodes in the BST";
else
cout << "K-th Smallest Element is " << res->data;
}
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int data;
struct Node *left, *right;
} Node;
struct Node* new_node(int x)
{
struct Node* p = malloc(sizeof(struct Node));
p->data = x;
p->left = NULL;
p->right = NULL;
return p;
}
Node* insert(Node* root, int x)
{
if (root == NULL)
return new_node(x);
if (x < root->data)
root->left = insert(root->left, x);
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
int count = 0;
Node* kthSmallest(Node* root, int k)
{
if (root == NULL)
return NULL;
Node* left = kthSmallest(root->left, k);
if (left != NULL)
return left;
count++;
if (count == k)
return root;
return kthSmallest(root->right, k);
}
void printKthSmallest(Node* root, int k)
{
Node* res = kthSmallest(root, k);
if (res == NULL)
printf("There are less than k nodes in the BST");
else
printf("K-th Smallest Element is %d", res->data);
}
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
int keys_size = sizeof(keys) / sizeof(keys[0]);
for (int i = 0; i < keys_size; i++)
root = insert(root, keys[i]);
int k = 3;
printKthSmallest(root, k);
return 0;
}
|
Java
import java.io.*;
class Node {
int data;
Node left, right;
Node(int x)
{
data = x;
left = right = null;
}
}
class GFG {
static int count = 0;
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
public static Node kthSmallest(Node root, int k)
{
if (root == null)
return null;
Node left = kthSmallest(root.left, k);
if (left != null)
return left;
count++;
if (count == k)
return root;
return kthSmallest(root.right, k);
}
public static void printKthSmallest(Node root, int k)
{
Node res = kthSmallest(root, k);
if (res == null)
System.out.println("There are less than k nodes in the BST");
else
System.out.println("K-th Smallest Element is " + res.data);
}
public static void main(String[] args)
{
Node root = null;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
}
}
|
Python3
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def insert(root, x):
if (root == None):
return Node(x)
if (x < root.data):
root.left = insert(root.left, x)
elif (x > root.data):
root.right = insert(root.right, x)
return root
def kthSmallest(root):
global k
if (root == None):
return None
left = kthSmallest(root.left)
if (left != None):
return left
k -= 1
if (k == 0):
return root
return kthSmallest(root.right)
def printKthSmallest(root):
res = kthSmallest(root)
if (res == None):
print("There are less than k nodes in the BST")
else:
print("K-th Smallest Element is ", res.data)
if __name__ == '__main__':
root = None
keys = [20, 8, 22, 4, 12, 10, 14]
for x in keys:
root = insert(root, x)
k = 3
printKthSmallest(root)
|
C#
using System;
class Node{
public int data;
public Node left, right;
public Node(int x)
{
data = x;
left = right = null;
}
}
class GFG{
static int count = 0;
public static Node insert(Node root,
int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
public static Node kthSmallest(Node root,
int k)
{
if (root == null)
return null;
Node left = kthSmallest(root.left, k);
if (left != null)
return left;
count++;
if (count == k)
return root;
return kthSmallest(root.right, k);
}
public static void printKthSmallest(Node root,
int k)
{
count = 0;
Node res = kthSmallest(root, k);
if (res == null)
Console.WriteLine("There are less " +
"than k nodes in the BST");
else
Console.WriteLine("K-th Smallest" +
" Element is " + res.data);
}
public static void Main(String[] args)
{
Node root = null;
int []keys = {20, 8, 22, 4,
12, 10, 14};
foreach (int x in keys)
root = insert(root, x);
int k = 3;
printKthSmallest(root, k);
}
}
|
Javascript
<script>
class Node
{
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
let count = 0;
function insert(root,x)
{
if (root == null)
return new Node(x);
if (x < root.data)
root.left = insert(root.left, x);
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
function kthSmallest(root,k)
{
if (root == null)
return null;
let left = kthSmallest(root.left, k);
if (left != null)
return left;
count++;
if (count == k)
return root;
return kthSmallest(root.right, k);
}
function printKthSmallest(root,k)
{
count = 0;
let res = kthSmallest(root, k);
if (res == null)
document.write("There are less "
+ "than k nodes in the BST");
else
document.write("K-th Smallest"
+ " Element is " + res.data);
}
let root=null;
let key=[20, 8, 22, 4, 12, 10, 14 ];
for(let i=0;i<key.length;i++)
{
root = insert(root, key[i]);
}
let k = 3;
printKthSmallest(root, k);
</script>
|
Output
K-th Smallest Element is 10
Time complexity: O(n) where n is the number of nodes in a binary search tree.
Auxiliary Space: O(h) where h is the height of the binary search tree.
We can optimize space using Morris Traversal. Please refer K’th smallest element in BST using O(1) Extra Space for details.
Method 2: Using Any Tree Traversal (pre-in-post) than return kth smallest easily.
Approach:
Here we use pre order traversal than sort it and return the kth smallest element.
Algorithm:
Here we have tree we will take preorder of it as :
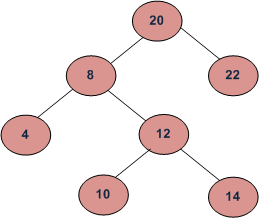
preorder will : 20 8 4 12 10 14 22
And store it in array/vector.
After taking preorder we will sort it and than return k-1 element from the array.
C++
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
int lCount;
Node(int x)
{
data = x;
left = right = NULL;
lCount = 0;
}
};
Node* insert(Node* root, int x)
{
if (root == NULL)
return new Node(x);
if (x < root->data) {
root->left = insert(root->left, x);
root->lCount++;
}
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
void preorder(Node* root,vector<int>&v){
if(root==NULL)return;
v.push_back(root->data);
preorder(root->left,v);
preorder(root->right,v);
}
int main(){
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
vector<int>v;
preorder(root,v);
sort(v.begin(),v.end());
cout<<v[k-1]<<endl;
return 0;
}
|
Java
import java.util.*;
class Node {
int data;
Node left, right;
int lCount;
Node(int x) {
data = x;
left = right = null;
lCount = 0;
}
}
public class KthSmallestElementBST {
static Node insert(Node root, int x) {
if (root == null)
return new Node(x);
if (x < root.data) {
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
static void preorder(Node root, List<Integer> v) {
if (root == null) return;
v.add(root.data);
preorder(root.left, v);
preorder(root.right, v);
}
public static void main(String[] args) {
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
List<Integer> v = new ArrayList<Integer>();
preorder(root, v);
Collections.sort(v);
System.out.println(v.get(k-1));
}
}
|
Python3
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
self.lCount = 0
def insert(root, x):
if root is None:
return Node(x)
if x < root.data:
root.left = insert(root.left, x)
root.lCount += 1
elif x > root.data:
root.right = insert(root.right, x)
return root
def preorder(root, v):
if root is None:
return
v.append(root.data)
preorder(root.left, v)
preorder(root.right, v)
if __name__ == '__main__':
root = None
keys = [20, 8, 22, 4, 12, 10, 14]
for x in keys:
root = insert(root, x)
k = 4
v = []
preorder(root, v)
v.sort()
print(v[k-1])
|
C#
using System;
using System.Collections.Generic;
class Program
{
class Node
{
public int data;
public Node left, right;
public int lCount;
public Node(int x)
{
data = x;
left = right = null;
lCount = 0;
}
}
static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
{
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
{
root.right = insert(root.right, x);
}
return root;
}
static void inorder(Node root, List<int> v)
{
if (root == null) return;
inorder(root.left, v);
v.Add(root.data);
inorder(root.right, v);
}
static void Main(string[] args)
{
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
foreach (int x in keys)
{
root = insert(root, x);
}
int k = 4;
List<int> v = new List<int>();
inorder(root, v);
Console.WriteLine(v[k - 1]);
}
}
|
Javascript
class Node {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
this.lCount = 0;
}
}
function insert(root, x) {
if (root === null) {
return new Node(x);
}
if (x < root.data) {
root.left = insert(root.left, x);
root.lCount++;
} else if (x > root.data) {
root.right = insert(root.right, x);
}
return root;
}
function preorder(root, v) {
if (root === null) {
return;
}
v.push(root.data);
preorder(root.left, v);
preorder(root.right, v);
}
let root = null;
const keys = [20, 8, 22, 4, 12, 10, 14];
for (const x of keys) {
root = insert(root, x);
}
const k = 4;
const v = [];
preorder(root, v);
v.sort((a, b) => a - b);
console.log(v[k - 1]);
|
Complexity Analysis:
Time Complexity: O(nlogn) i.e O(n) time for preorder and nlogn time for sorting.
Auxiliary Space: O(n) i.e for vector/array storage.
Method 3: Augmented Tree Data Structure (O(h) Time Complexity and O(h) auxiliary space)
The idea is to maintain the rank of each node. We can keep track of elements in the left subtree of every node while building the tree. Since we need the K-th smallest element, we can maintain the number of elements of the left subtree in every node.
Assume that the root is having ‘lCount’ nodes in its left subtree. If K = lCount + 1, root is K-th node. If K < lCount + 1, we will continue our search (recursion) for the Kth smallest element in the left subtree of root. If K > lCount + 1, we continue our search in the right subtree for the (K – lCount – 1)-th smallest element. Note that we need the count of elements in the left subtree only.
C++
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
int lCount;
Node(int x)
{
data = x;
left = right = NULL;
lCount = 0;
}
};
Node* insert(Node* root, int x)
{
if (root == NULL)
return new Node(x);
if (x < root->data) {
root->left = insert(root->left, x);
root->lCount++;
}
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
Node* kthSmallest(Node* root, int k)
{
if (root == NULL)
return NULL;
int count = root->lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root->left, k);
return kthSmallest(root->right, k - count);
}
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
Node* res = kthSmallest(root, k);
if (res == NULL)
cout << "There are less than k nodes in the BST";
else
cout << "K-th Smallest Element is " << res->data;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int data;
struct Node *left, *right;
int lCount;
} Node;
Node* new_node(int x)
{
Node* newNode = malloc(sizeof(Node));
newNode->data = x;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
Node* insert(Node* root, int x)
{
if (root == NULL)
return new_node(x);
if (x < root->data) {
root->left = insert(root->left, x);
root->lCount++;
}
else if (x > root->data)
root->right = insert(root->right, x);
return root;
}
Node* kthSmallest(Node* root, int k)
{
if (root == NULL)
return NULL;
int count = root->lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root->left, k);
return kthSmallest(root->right, k - count);
}
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
int keys_size = sizeof(keys) / sizeof(keys[0]);
for (int i = 0; i < keys_size; i++)
root = insert(root, keys[i]);
int k = 4;
Node* res = kthSmallest(root, k);
if (res == NULL)
printf("There are less than k nodes in the BST");
else
printf("K-th Smallest Element is %d", res->data);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class Node {
int data;
Node left, right;
int lCount;
Node(int x)
{
data = x;
left = right = null;
lCount = 0;
}
}
class Gfg {
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
if (x < root.data) {
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
public static Node kthSmallest(Node root, int k)
{
if (root == null)
return null;
int count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
return kthSmallest(root.right, k - count);
}
public static void main(String args[])
{
Node root = null;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
Node res = kthSmallest(root, k);
if (res == null)
System.out.println("There are less than k nodes in the BST");
else
System.out.println("K-th Smallest Element is " + res.data);
}
}
|
Python3
class newNode:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
self.lCount = 0
def insert(root, x):
if (root == None):
return newNode(x)
if (x < root.data):
root.left = insert(root.left, x)
root.lCount += 1
elif (x > root.data):
root.right = insert(root.right, x);
return root
def kthSmallest(root, k):
if (root == None):
return None
count = root.lCount + 1
if (count == k):
return root
if (count > k):
return kthSmallest(root.left, k)
return kthSmallest(root.right, k - count)
if __name__ == '__main__':
root = None
keys = [ 20, 8, 22, 4, 12, 10, 14 ]
for x in keys:
root = insert(root, x)
k = 4
res = kthSmallest(root, k)
if (res == None):
print("There are less than k nodes in the BST")
else:
print("K-th Smallest Element is", res.data)
|
C#
using System;
public class Node
{
public int data;
public Node left, right;
public int lCount;
public Node(int x)
{
data = x;
left = right = null;
lCount = 0;
}
}
class GFG{
public static Node insert(Node root, int x)
{
if (root == null)
return new Node(x);
if (x < root.data)
{
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
public static Node kthSmallest(Node root, int k)
{
if (root == null)
return null;
int count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
return kthSmallest(root.right, k - count);
}
public static void Main(String[] args)
{
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
foreach(int x in keys)
root = insert(root, x);
int k = 4;
Node res = kthSmallest(root, k);
if (res == null)
Console.WriteLine("There are less " +
"than k nodes in the BST");
else
Console.WriteLine("K-th Smallest" +
" Element is " + res.data);
}
}
|
Javascript
<script>
class Node
{
constructor(x)
{
this.data = x;
this.left = null;
this.right = null;
this.lCount = 0;
}
}
function insert(root, x)
{
if (root == null)
return new Node(x);
if (x < root.data)
{
root.left = insert(root.left, x);
root.lCount++;
}
else if (x > root.data)
root.right = insert(root.right, x);
return root;
}
function kthSmallest(root, k)
{
if (root == null)
return null;
let count = root.lCount + 1;
if (count == k)
return root;
if (count > k)
return kthSmallest(root.left, k);
return kthSmallest(root.right, k - count);
}
let root = null;
let keys = [ 20, 8, 22, 4, 12, 10, 14 ];
for(let x = 0; x < keys.length; x++)
root = insert(root, keys[x]);
let k = 4;
let res = kthSmallest(root, k);
if (res == null)
document.write("There are less than k " +
"nodes in the BST" + "</br>");
else
document.write("K-th Smallest" +
" Element is " + res.data);
</script>
|
Output
K-th Smallest Element is 12
Time complexity: O(h) where h is the height of the tree.
Auxiliary Space: O(h)
Method 4: Iterative approach using Stack: The basic idea behind the Iterative Approach using Stack to find the kth smallest element in a Binary Search Tree (BST) is to traverse the tree in an inorder fashion using a stack until we find the kth smallest element. Follow the steps to implement the above idea:
- Create an empty stack and set the current node to the root of the BST.
- Push all the left subtree nodes of the current node onto the stack until the current node is NULL.
- Pop the top node from the stack and check if it is the k-th element. If it is, return its value.
- Decrement the value of k by 1.
- Set the current node to the right child of the popped node.
- Go to step 2 if the stack is not empty or k is not equal to 0.
Below is the implementation of the above approach:
C++
#include <iostream>
#include <stack>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* newNode(int key)
{
Node* node = new Node;
node->data = key;
node->left = node->right = NULL;
return node;
}
Node* insert(Node* root, int key)
{
if (root == NULL)
return newNode(key);
if (key < root->data)
root->left = insert(root->left, key);
else if (key > root->data)
root->right = insert(root->right, key);
return root;
}
int kthSmallest(Node* root, int k)
{
stack<Node*> s;
while (root != NULL || !s.empty()) {
while (root != NULL) {
s.push(root);
root = root->left;
}
root = s.top();
s.pop();
if (--k == 0)
return root->data;
root = root->right;
}
return -1;
}
int main()
{
Node* root = NULL;
int keys[] = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
int kth_smallest = kthSmallest(root, k);
if (kth_smallest != -1)
cout << "K-th smallest element in BST is: "
<< kth_smallest << endl;
else
cout << "Invalid input" << endl;
return 0;
}
|
Java
import java.util.Stack;
class Node {
int data;
Node left, right;
Node(int key) {
data = key;
left = right = null;
}
}
class GFG {
static Node insert(Node root, int key) {
if (root == null)
return new Node(key);
if (key < root.data)
root.left = insert(root.left, key);
else if (key > root.data)
root.right = insert(root.right, key);
return root;
}
static int kthSmallest(Node root, int k) {
Stack<Node> stack = new Stack<>();
while (root != null || !stack.empty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (--k == 0)
return root.data;
root = root.right;
}
return -1;
}
public static void main(String[] args) {
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
for (int x : keys)
root = insert(root, x);
int k = 4;
int kth_smallest = kthSmallest(root, k);
if (kth_smallest != -1)
System.out.println("K-th smallest element in BST is: " + kth_smallest);
else
System.out.println("Invalid input");
}
}
|
Python3
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def insert(root, key):
if root is None:
return Node(key)
if key < root.data:
root.left = insert(root.left, key)
elif key > root.data:
root.right = insert(root.right, key)
return root
def kthSmallest(root, k):
stack = []
while root is not None or len(stack) > 0:
while root is not None:
stack.append(root)
root = root.left
root = stack.pop()
k -= 1
if k == 0:
return root.data
root = root.right
return -1
if __name__ == '__main__':
root = None
keys = [20, 8, 22, 4, 12, 10, 14]
for x in keys:
root = insert(root, x)
k = 4
kth_smallest = kthSmallest(root, k)
if kth_smallest != -1:
print("K-th smallest element in BST is:", kth_smallest)
else:
print("Invalid input")
|
C#
using System;
using System.Collections.Generic;
public class Node
{
public int data;
public Node left, right;
public Node(int key)
{
data = key;
left = right = null;
}
}
public class BinarySearchTree
{
public static Node Insert(Node root, int key)
{
if (root == null)
return new Node(key);
if (key < root.data)
root.left = Insert(root.left, key);
else if (key > root.data)
root.right = Insert(root.right, key);
return root;
}
public static int KthSmallest(Node root, int k)
{
Stack<Node> stack = new Stack<Node>();
while (root != null || stack.Count > 0)
{
while (root != null)
{
stack.Push(root);
root = root.left;
}
root = stack.Pop();
if (--k == 0)
return root.data;
root = root.right;
}
return -1;
}
public static void Main()
{
Node root = null;
int[] keys = { 20, 8, 22, 4, 12, 10, 14 };
foreach (int key in keys)
root = Insert(root, key);
int k = 4;
int kth_smallest = KthSmallest(root, k);
if (kth_smallest != -1)
Console.WriteLine("K-th smallest element in BST is: " + kth_smallest);
else
Console.WriteLine("Invalid input");
}
}
|
Javascript
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function insert(root, key) {
if (root === null)
return new Node(key);
if (key < root.data)
root.left = insert(root.left, key);
else if (key > root.data)
root.right = insert(root.right, key);
return root;
}
function kthSmallest(root, k) {
const stack = [];
while (root !== null || stack.length > 0) {
while (root !== null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (--k === 0)
return root.data;
root = root.right;
}
return -1;
}
let root = null;
const keys = [20, 8, 22, 4, 12, 10, 14];
for (const x of keys)
root = insert(root, x);
const k = 4;
const kth_smallest = kthSmallest(root, k);
if (kth_smallest !== -1)
console.log("K-th smallest element in BST is: " + kth_smallest);
else
console.log("Invalid input");
|
Output
K-th smallest element in BST is: 12
Time Complexity: O(h+ k), The time complexity of the Iterative Approach using Stack to find the kth smallest element in a BST is O(h + k), where h is the height of the BST and k is the value of k.
Auxiliary Space: O(h+k), The space complexity of the code is O(h + k), where h is the height of the BST and k is the maximum size of the stack.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...