Find if there is a path of more than k length from a source
Last Updated :
10 Jul, 2023
Given a graph, a source vertex in the graph and a number k, find if there is a simple path (without any cycle) starting from given source and ending at any other vertex such that the distance from source to that vertex is atleast ‘k’ length.
Example:
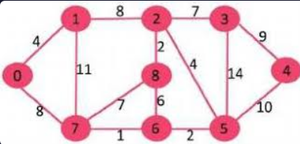
Weighted Undirected Graph
Input : Source s = 0, k = 58
Output : True
There exists a simple path 0 -> 7 -> 1
-> 2 -> 8 -> 6 -> 5 -> 3 -> 4
Which has a total distance of 60 km which
is more than 58.
Input : Source s = 0, k = 62
Output : False
In the above graph, the longest simple
path has distance 61 (0 -> 7 -> 1-> 2
-> 3 -> 4 -> 5-> 6 -> 8, so output
should be false for any input greater
than 61.
We strongly recommend you to minimize your browser and try this yourself first.
One important thing to note is, simply doing BFS or DFS and picking the longest edge at every step would not work. The reason is, a shorter edge can produce longer path due to higher weight edges connected through it.
The idea is to use Backtracking. We start from given source, explore all paths from current vertex. We keep track of current distance from source. If distance becomes more than k, we return true. If a path doesn’t produces more than k distance, we backtrack.
How do we make sure that the path is simple and we don’t loop in a cycle? The idea is to keep track of current path vertices in an array. Whenever we add a vertex to path, we check if it already exists or not in current path. If it exists, we ignore the edge.
Below is implementation of above idea.
Java
import java.util.*;
public class GFG{
static class AdjListNode {
int v;
int weight;
AdjListNode(int _v, int _w)
{
v = _v;
weight = _w;
}
int getV() { return v; }
int getWeight() { return weight; }
}
static class Graph
{
int V;
ArrayList<ArrayList<AdjListNode>> adj;
Graph(int V)
{
this.V = V;
adj = new ArrayList<ArrayList<AdjListNode>>(V);
for(int i = 0; i < V; i++)
{
adj.add(new ArrayList<AdjListNode>());
}
}
void addEdge(int u, int v, int weight)
{
AdjListNode node1 = new AdjListNode(v, weight);
adj.get(u).add(node1);
AdjListNode node2 = new AdjListNode(u, weight);
adj.get(v).add(node2);
}
boolean pathMoreThanK(int src, int k)
{
boolean path[] = new boolean[V];
Arrays.fill(path, false);
path[src] = true;
return pathMoreThanKUtil(src, k, path);
}
boolean pathMoreThanKUtil(int src, int k, boolean[] path)
{
if (k <= 0)
return true;
ArrayList<AdjListNode> it = adj.get(src);
int index = 0;
for(int i = 0; i < adj.get(src).size(); i++)
{
AdjListNode vertex = adj.get(src).get(i);
int v = vertex.v;
int w = vertex.weight;
index++;
if (path[v] == true)
continue;
if (w >= k)
return true;
path[v] = true;
if (pathMoreThanKUtil(v, k-w, path))
return true;
path[v] = false;
}
return false;
}
}
public static void main(String[] args)
{
int V = 9;
Graph g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
int k = 62;
if(g.pathMoreThanK(src, k))
System.out.println("YES");
else
System.out.println("NO");
k = 60;
if(g.pathMoreThanK(src, k))
System.out.println("YES");
else
System.out.println("NO");
}
}
|
Python3
class Graph:
def __init__(self, V):
self.V = V
self.adj = [[] for i in range(V)]
def pathMoreThanK(self,src, k):
path = [False]*self.V
path[src] = 1
return self.pathMoreThanKUtil(src, k, path)
def pathMoreThanKUtil(self,src, k, path):
if (k <= 0):
return True
i = 0
while i != len(self.adj[src]):
v = self.adj[src][i][0]
w = self.adj[src][i][1]
i += 1
if (path[v] == True):
continue
if (w >= k):
return True
path[v] = True
if (self.pathMoreThanKUtil(v, k-w, path)):
return True
path[v] = False
return False
def addEdge(self,u, v, w):
self.adj[u].append([v, w])
self.adj[v].append([u, w])
if __name__ == '__main__':
V = 9
g = Graph(V)
g.addEdge(0, 1, 4)
g.addEdge(0, 7, 8)
g.addEdge(1, 2, 8)
g.addEdge(1, 7, 11)
g.addEdge(2, 3, 7)
g.addEdge(2, 8, 2)
g.addEdge(2, 5, 4)
g.addEdge(3, 4, 9)
g.addEdge(3, 5, 14)
g.addEdge(4, 5, 10)
g.addEdge(5, 6, 2)
g.addEdge(6, 7, 1)
g.addEdge(6, 8, 6)
g.addEdge(7, 8, 7)
src = 0
k = 62
if g.pathMoreThanK(src, k):
print("Yes")
else:
print("No")
k = 60
if g.pathMoreThanK(src, k):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class Program
{
static void Main(string[] args)
{
int V = 9;
Graph g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
int k = 62;
if (g.pathMoreThanK(src, k))
Console.WriteLine("YES");
else
Console.WriteLine("NO");
k = 60;
if (g.pathMoreThanK(src, k))
Console.WriteLine("YES");
else
Console.WriteLine("NO");
}
}
class AdjListNode {
public int v;
public int weight;
public AdjListNode(int _v, int _w)
{
v = _v;
weight = _w;
}
public int getV() { return v; }
public int getWeight() { return weight; }
}
class Graph {
public int V;
public List<List<AdjListNode> > adj
= new List<List<AdjListNode> >();
public Graph(int V)
{
this.V = V;
for (int i = 0; i < V; i++)
adj.Add(new List<AdjListNode>());
}
public void addEdge(int u, int v, int weight)
{
AdjListNode node1 = new AdjListNode(v, weight);
adj[u].Add(node1);
AdjListNode node2 = new AdjListNode(u, weight);
adj[v].Add(node2);
}
bool pathMoreThanKUtil(int src, int k, bool[] path)
{
if (k <= 0)
return true;
List<AdjListNode> it = adj[src];
for (int i = 0; i < adj[src].Count; i++) {
AdjListNode vertex = adj[src][i];
int v = vertex.v;
int w = vertex.weight;
if (path[v] == true)
continue;
if (w >= k)
return true;
path[v] = true;
if (pathMoreThanKUtil(v, k - w, path))
return true;
path[v] = false;
}
return false;
}
public bool pathMoreThanK(int src, int k)
{
bool[] path = new bool[V];
for (int i = 0; i < V; i++)
path[i] = false;
path[src] = true;
return pathMoreThanKUtil(src, k, path);
}
}
|
Javascript
class AdjListNode {
constructor(v, weight) {
this.v = v;
this.weight = weight;
}
}
class Graph {
constructor(V) {
this.V = V;
this.adj = [];
for (var i = 0; i < V; i++) {
this.adj[i] = [];
}
}
addEdge(u, v, weight) {
var node1 = new AdjListNode(v, weight);
this.adj[u].push(node1);
var node2 = new AdjListNode(u, weight);
this.adj[v].push(node2);
}
pathMoreThanKUtil(src, k, path) {
if (k <= 0)
return true;
var it = this.adj[src];
for (var i = 0; i < this.adj[src].length; i++) {
var vertex = this.adj[src][i];
var v = vertex.v;
var w = vertex.weight;
if (path[v] == true)
continue;
if (w >= k)
return true;
path[v] = true;
if (this.pathMoreThanKUtil(v, k - w, path))
return true;
path[v] = false;
}
return false;
}
pathMoreThanK(src, k) {
var path = new Array(V);
for (var i = 0; i < V; i++) {
path[i] = false;
}
path[src] = true;
return this.pathMoreThanKUtil(src, k, path);
}
}
var V = 9;
var g = new Graph(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
var src = 0;
var k = 62;
if (g.pathMoreThanK(src, k)) {
console.log("YES");
} else {
console.log("NO");
}
k = 60
if (g.pathMoreThanK(src, k)) {
console.log("YES");
} else {
console.log("NO");
}
|
C++
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> iPair;
class Graph
{
int V;
list< pair<int, int> > *adj;
bool pathMoreThanKUtil(int src, int k, vector<bool> &path);
public:
Graph(int V);
void addEdge(int u, int v, int w);
bool pathMoreThanK(int src, int k);
};
bool Graph::pathMoreThanK(int src, int k)
{
vector<bool> path(V, false);
path[src] = 1;
return pathMoreThanKUtil(src, k, path);
}
bool Graph::pathMoreThanKUtil(int src, int k, vector<bool> &path)
{
if (k <= 0)
return true;
list<iPair>::iterator i;
for (i = adj[src].begin(); i != adj[src].end(); ++i)
{
int v = (*i).first;
int w = (*i).second;
if (path[v] == true)
continue;
if (w >= k)
return true;
path[v] = true;
if (pathMoreThanKUtil(v, k-w, path))
return true;
path[v] = false;
}
return false;
}
Graph::Graph(int V)
{
this->V = V;
adj = new list<iPair> [V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
int main()
{
int V = 9;
Graph g(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
int k = 62;
g.pathMoreThanK(src, k)? cout << "Yes\n" :
cout << "No\n";
k = 60;
g.pathMoreThanK(src, k)? cout << "Yes\n" :
cout << "No\n";
return 0;
}
|
Output:
No
Yes
Exercise:
Modify the above solution to find weight of longest path from a given source.
Time Complexity: The time complexity of this algorithm is O((V-1)!) where V is the number of vertices.
Auxiliary Space: O(V)
Explanation:
From the source node, we one-by-one visit all the paths and check if the total weight is greater than k for each path. So, the worst case will be when the number of possible paths is maximum. This is the case when every node is connected to every other node.
Since the starting point is fixed, we need to find a path including all the other vertices. There can be (V-1) choices for the second node, (V-2) choices for the third node, and so on till, 1 choice for the last node.
Therefore the total number of possible paths are (V-1)! in the worst case.
In the recursive call, when we reach a node, we again do recursive call for all of its child. Changing the state of array(which stores whether the node is visited or not), takes O(1) time.
So the time complexity becomes O((V-1)!).
The explanation for time complexity is contributed by Pranav Nambiar, and Aayush Patel.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...