Find if it is possible to get a ratio from given ranges of costs and quantities
Last Updated :
20 Feb, 2023
Given the range of cost from lowCost to upCost and range of quantity from lowQuant to upQuant, find if it is possible to get a given ration ratio r where  , and lowCost <= cost <= upCost and lowQuant <= quantity <= upQuant.
, and lowCost <= cost <= upCost and lowQuant <= quantity <= upQuant.
Examples :
Input : lowCost = 1, upCost = 10,
lowQuant = 2, upQuant = 8
r = 3
Output : Yes
Explanation:
cost / quantity = 6 / 2 = 3
where cost is in [1, 10] and quantity
is in [2, 8]
Input : lowCost = 14, upCost = 30,
lowQuant = 5, upQuant = 12
r = 9
Output : No
Approach: From the given formula, following equation can be easily deduced: 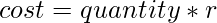 .
.
From this equation, logic can be easily deduced. Check the product of every value of quantity with r and if any value of the product lies between lowCost and upCost, then answer is Yes otherwise it is No.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isRatioPossible(int lowCost, int upCost,
int lowQuant, int upQuant,
int r)
{
for (int i = lowQuant; i <= upQuant; i++)
{
int ans = i * r;
if (lowCost <= ans && ans <= upCost)
return true;
}
return false;
}
int main()
{
int lowCost = 14, upCost = 30,
lowQuant = 5, upQuant = 12,
r = 9;
if (isRatioPossible(lowCost, upCost,
lowQuant, upQuant, r))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
import java.io.*;
class Ratio
{
static boolean isRatioPossible(int lowCost, int upCost,
int lowQuant, int upQuant,
int r)
{
for (int i = lowQuant; i <= upQuant; i++)
{
int ans = i * r;
if (lowCost <= ans && ans <= upCost)
return true;
}
return false;
}
public static void main(String args[])
{
int lowCost = 14, upCost = 30,
lowQuant = 5, upQuant = 12, r = 9;
if (isRatioPossible(lowCost, upCost,
lowQuant, upQuant, r))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def isRatioPossible(lowCost, upCost,
lowQuant, upQuant, r) :
for i in range(lowQuant, upQuant + 1) :
ans = i * r
if (lowCost <= ans and ans <= upCost) :
return True
return False
lowCost = 14; upCost = 30
lowQuant = 5; upQuant = 12; r = 9
if (isRatioPossible(lowCost, upCost,
lowQuant,upQuant, r)) :
print( "Yes" )
else :
print( "No" )
|
C#
using System;
class Ratio
{
static bool isRatioPossible(int lowCost, int upCost,
int lowQuant, int upQuant,
int r)
{
for (int i = lowQuant; i <= upQuant; i++)
{
int ans = i * r;
if (lowCost <= ans && ans <= upCost)
return true;
}
return false;
}
public static void Main()
{
int lowCost = 14, upCost = 30,
lowQuant = 5, upQuant = 12, r = 9;
if (isRatioPossible(lowCost, upCost,
lowQuant, upQuant, r))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
PHP
<?php
function isRatioPossible($lowCost, $upCost,
$lowQuant, $upQuant,$r)
{
for ($i = $lowQuant; $i <= $upQuant; $i++)
{
$ans = $i * $r;
if ($lowCost <= $ans && $ans <= $upCost)
return true;
}
return false;
}
$lowCost = 14; $upCost = 30;
$lowQuant = 5; $upQuant = 12; $r = 9;
if (isRatioPossible($lowCost, $upCost,
$lowQuant, $upQuant, $r))
echo "Yes";
else
echo "No";
# This code is contributed by ajit
?>
|
Javascript
<script>
function isRatioPossible(lowCost, upCost,
lowQuant, upQuant,
r)
{
for (let i = lowQuant; i <= upQuant; i++)
{
let ans = i * r;
if (lowCost <= ans && ans <= upCost)
return true;
}
return false;
}
let lowCost = 14, upCost = 30,
lowQuant = 5, upQuant = 12, r = 9;
if (isRatioPossible(lowCost, upCost,
lowQuant, upQuant, r))
document.write("Yes");
else
document.write("No");
</script>
|
Output :
No
Time Complexity: O(|uq-lq|), where uq is upQuant and lq is lowQuant.
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...