Find if given matrix is Toeplitz or not
Last Updated :
30 Jan, 2023
Given a square matrix, find if it’s a Toeplitz matrix or not. A Toeplitz (or diagonal-constant) matrix is a matrix in which each descending diagonal from left to right is constant, i.e., all elements in a diagonal are same.
In general, any n×n matrix mat[][] is a Toeplitz matrix if every cell mat[i][j] is same as mat[i-1][j-1], mat[i+1][j+1], mat[i-2][j-2], mat[i+2][j+2], .. for every cell mat[i][j] and all the valid cells mat[i+k][j+k] or mat[i-k][j-k]
Examples :
Input: mat[N][N] = {{ 6, 7, 8},
{ 4, 6, 7},
{ 1, 4, 6}},
Output : True;
Values in all diagonals are same.
Input: mat[N][N] = {{ 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 }};
Output : True;
Input: mat[N][N] = {{ 6, 3, 8},
{ 4, 9, 7},
{ 1, 4, 6}},
Output : False;
The idea is very simple. For each element of first row and first column(or last row and last column) in the matrix, we check if descending diagonal starting from that element have same values or not. If we found any diagonal having different values, we return false.
Below is the implementation of the above code:
C++
#include <iostream>
using namespace std;
#define N 5
#define M 4
bool checkDiagonal(int mat[N][M], int i, int j)
{
int res = mat[i][j];
while (++i < N && ++j < M)
{
if (mat[i][j] != res)
return false;
}
return true;
}
bool isToeplitz(int mat[N][M])
{
for (int i = 0; i < M; i++)
{
if (!checkDiagonal(mat, 0, i))
return false;
}
for (int i = 1; i < N; i++)
{
if (!checkDiagonal(mat, i, 0))
return false;
}
return true;
}
int main()
{
int mat[N][M] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
cout << "Matrix is a Toeplitz ";
else
cout << "Matrix is not a Toeplitz ";
return 0;
}
|
Java
import java.io.*;
class GFG
{
public static int N = 5;
public static int M = 4;
static boolean checkDiagonal(int mat[][], int i, int j)
{
int res = mat[i][j];
while (++i < N && ++j < M)
{
if (mat[i][j] != res)
return false;
}
return true;
}
static boolean isToeplitz(int mat[][])
{
for (int i = 0; i < M; i++)
{
if (!checkDiagonal(mat, 0, i))
return false;
}
for (int i = 1; i < N; i++)
{
if (!checkDiagonal(mat, i, 0))
return false;
}
return true;
}
public static void main(String[] args)
{
int mat[][] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
System.out.println("Matrix is a Toeplitz ");
else
System.out.println("Matrix is not a Toeplitz ");
}
}
|
Python3
N = 5
M = 4
def checkDiagonal(mat, i, j):
res = mat[i][j]
i += 1
j += 1
while (i < N and j < M):
if (mat[i][j] != res):
return False
i += 1
j += 1
return True
def isToeplitz(mat):
for j in range(M):
if not(checkDiagonal(mat, 0, j)):
return False
for i in range(1, N):
if not(checkDiagonal(mat, i, 0)):
return False
return True
if __name__ == "__main__":
mat = [[6, 7, 8, 9],
[4, 6, 7, 8],
[1, 4, 6, 7],
[0, 1, 4, 6],
[2, 0, 1, 4]]
if(isToeplitz(mat)):
print("Matrix is a Toeplitz")
else:
print("Matrix is not a Toeplitz")
|
C#
using System;
class GFG {
public static int N = 5;
public static int M = 4;
static bool checkDiagonal(int[, ] mat, int i, int j)
{
int res = mat[i, j];
while (++i < N && ++j < M) {
if (mat[i, j] != res)
return false;
}
return true;
}
static bool isToeplitz(int[, ] mat)
{
for (int i = 0; i < M; i++) {
if (!checkDiagonal(mat, 0, i))
return false;
}
for (int i = 1; i < N; i++) {
if (!checkDiagonal(mat, i, 0))
return false;
}
return true;
}
public static void Main()
{
int[, ] mat = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
Console.WriteLine("Matrix is a Toeplitz ");
else
Console.WriteLine("Matrix is not a Toeplitz ");
}
}
|
PHP
<?php
function checkDiagonal($mat, $i, $j)
{
$N = 5; $M = 4;
$res = $mat[$i][$j];
while (++$i < $N && ++$j < $M)
{
if ($mat[$i][$j] != $res)
return false;
}
return true;
}
function isToeplitz($mat)
{
$N = 5; $M = 4;
for ($i = 0; $i < $M; $i++)
{
if (!checkDiagonal($mat, 0, $i))
return false;
}
for ($i = 1; $i < $N; $i++)
{
if (!checkDiagonal($mat, $i, 0))
return false;
}
return true;
}
$mat = array(array( 6, 7, 8, 9 ),
array( 4, 6, 7, 8 ),
array( 1, 4, 6, 7 ),
array( 0, 1, 4, 6 ),
array( 2, 0, 1, 4 ));
if (isToeplitz($mat))
echo "Matrix is a Toeplitz ";
else
echo "Matrix is not a Toeplitz ";
?>
|
Javascript
<script>
let N = 5;
let M = 4;
function checkDiagonal(mat, i, j)
{
let res = mat[i][j];
while (++i < N && ++j < M)
{
if (mat[i][j] != res)
return false;
}
return true;
}
function isToeplitz(mat)
{
for (let i = 0; i < M; i++)
{
if (!checkDiagonal(mat, 0, i))
return false;
}
for (let i = 1; i < N; i++)
{
if (!checkDiagonal(mat, i, 0))
return false;
}
return true;
}
let mat = [ [ 6, 7, 8, 9 ],
[ 4, 6, 7, 8 ],
[ 1, 4, 6, 7 ],
[ 0, 1, 4, 6 ],
[ 2, 0, 1, 4 ] ];
if (isToeplitz(mat))
document.write("Matrix is a Toeplitz ");
else
document.write("Matrix is not a Toeplitz ");
</script>
|
Output
Matrix is a Toeplitz
The time complexity of this solution would be O(mn) where m is number of rows and n is number of columns as we are traversing through each element of the matrix.
Auxiliary Space: O(1), since no extra space has been taken.
This approach can further be improved:
As we can see that we are traversing through entire matrix so we will keep track of each element if it is equal to its diagonally above element or not. If any element fails this condition this means matrix is not “Toeplitz” so return false or if all elements pass this condition then return true.
C++
#include <iostream>
using namespace std;
#define N 5
#define M 4
bool isToeplitz(int matrix[N][M])
{
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
if (matrix[i][j] != matrix[i - 1][j - 1])
return false;
}
}
return true;
}
int main()
{
int mat[N][M] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
cout << "Matrix is a Toeplitz ";
else
cout << "Matrix is not a Toeplitz ";
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int N = 5;
public static int M = 4;
static boolean isToeplitz(int mat[][])
{
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
if (mat[i][j] != mat[i - 1][j - 1]) {
return false;
}
}
}
return true;
}
public static void main(String[] args)
{
int mat[][] = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
System.out.println("Matrix is a Toeplitz ");
else
System.out.println("Matrix is not a Toeplitz ");
}
}
|
Python3
N=5;
M=4;
def isToeplitz( matrix):
for i in range(1,N):
for j in range(1,M):
if (matrix[i][j] != matrix[i - 1][j - 1]):
return False;
return True;
mat = [ [ 6, 7, 8, 9 ],
[ 4, 6, 7, 8 ],
[ 1, 4, 6, 7 ],
[ 0, 1, 4, 6 ],
[ 2, 0, 1, 4 ] ];
if (isToeplitz(mat)):
print("Matrix is a Toeplitz ");
else:
print("Matrix is not a Toeplitz ");
|
C#
using System;
class GFG {
public static int N = 5;
public static int M = 4;
static bool isToeplitz(int[, ] mat)
{
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
if (mat[i, j] != mat[i - 1, j - 1]) {
return false;
}
}
}
return true;
}
public static void Main(string[] args)
{
int[, ] mat = { { 6, 7, 8, 9 },
{ 4, 6, 7, 8 },
{ 1, 4, 6, 7 },
{ 0, 1, 4, 6 },
{ 2, 0, 1, 4 } };
if (isToeplitz(mat))
Console.WriteLine("Matrix is a Toeplitz ");
else
Console.WriteLine("Matrix is not a Toeplitz ");
}
}
|
Javascript
const N = 5
const M = 4
function isToeplitz(matrix)
{
for (let i = 1; i < N; i++) {
for (let j = 1; j < M; j++) {
if (matrix[i][j] != matrix[i - 1][j - 1])
return false;
}
}
return true;
}
let mat = [ [ 6, 7, 8, 9 ],
[ 4, 6, 7, 8 ],
[ 1, 4, 6, 7 ],
[ 0, 1, 4, 6 ],
[ 2, 0, 1, 4 ] ];
if (isToeplitz(mat))
document.write("Matrix is a Toeplitz ");
else
document.write("Matrix is not a Toeplitz ");
|
Output
Matrix is a Toeplitz
Time complexity of this solution would be O(mn) where m is number of rows and n is number of columns as we are traversing through each element of the matrix.
Auxiliary Space: O(1), since no extra space has been taken.
Hashing based approach:
Consider an element at index (i, j) of matrix of dimension (m, n). For the matrix to be diagonal-constant, all the elements in the diagonal must be same. Consider the diagonal containing this (i, j) element. The other elements in this diagonal will have their index of the form (i+k, j+k) or (i-k, j-k). Notice that whatever x-value and y-value of these indexes are, their difference is always the same. i.e. (i+k)-(j+k) == (i-k)-(j-k) == i-j.
The diagram below gives a better visualization of this idea. Consider the diagonal coloured yellow. The difference between x-value and y-value of any index on this diagonal is 2 (2-0, 3-1, 4-2, 5-3). Same can be observed for all body diagonals.
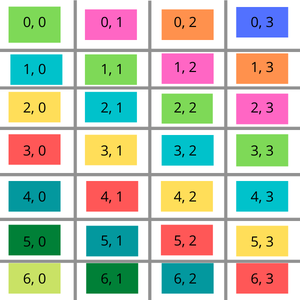
Index of a Toeplitz matrix
For red-coloured diagonal, difference is 3. For green-coloured diagonal, difference is 0. For orange-coloured diagonal, difference is -2 and so on…
The idea is to exploit the fact that for a Toeplitz matrix, these individual index differences for particular diagonals will be unique. And since it is a constant-diagonal matrix, for all these unique keys, there should be unique values same as any element on that diagonal. So, we create a HashMap to store these (key, value) pairs. At any moment if we encounter a value, that is different from it’s corresponding stored key value, we return false.
Below is the implementation of the above code:
C++
#include <bits/stdc++.h>
using namespace std;
bool isToeplitz(vector<vector<int>> matrix)
{
int row = matrix.size();
int col = matrix[0].size();
map<int, int> Map;
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
int key = i - j;
if (Map[key])
{
if (Map[key] != matrix[i][j])
return false;
}
else
{
Map[i - j] = matrix[i][j];
}
}
}
return true;
}
int main()
{
vector<vector<int>> matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
string result = (isToeplitz(matrix)) ? "Yes" : "No";
cout << result;
return 0;
}
|
Java
import java.util.*;
class GFG {
static boolean isToeplitz(int[][] matrix)
{
int row = matrix.length;
int col = matrix[0].length;
HashMap<Integer, Integer> map
= new HashMap<Integer, Integer>();
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
int key = i - j;
if (map.containsKey(key))
{
if (map.get(key) != matrix[i][j])
return false;
}
else {
map.put(i - j, matrix[i][j]);
}
}
}
return true;
}
public static void main(String[] args)
{
int[][] matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
String result = (isToeplitz(matrix)) ? "Yes" : "No";
System.out.println(result);
}
}
|
Python3
def isToeplitz(matrix):
row = len(matrix)
col = len(matrix[0])
map = {}
for i in range(row):
for j in range(col):
key = i-j
if (key in map):
if (map[key] != matrix[i][j]):
return False
else:
map[key] = matrix[i][j]
return True
if __name__ == "__main__":
matrix = [[12, 23, -32], [-20, 12, 23], [56, -20, 12], [38, 56, -20]]
if (isToeplitz(matrix)):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG{
static bool isToeplitz(int[,] matrix)
{
int row = matrix.GetLength(0);
int col = matrix.GetLength(1);
Dictionary<int,
int> map = new Dictionary<int,
int>();
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
int key = i - j;
if (map.ContainsKey(key))
{
if (map[key] != matrix[i, j])
return false;
}
else
{
map.Add(i - j, matrix[i, j]);
}
}
}
return true;
}
static void Main()
{
int[,] matrix = { { 12, 23, -32 },
{ -20, 12, 23 },
{ 56, -20, 12 },
{ 38, 56, -20 } };
string result = (isToeplitz(matrix)) ?
"Yes" : "No";
Console.WriteLine(result);
}
}
|
Javascript
<script>
function isToeplitz(matrix)
{
let row = matrix.length;
let col = matrix[0].length;
let map = new Map();
for(let i = 0; i < row; i++)
{
for(let j = 0; j < col; j++)
{
let key = i - j;
if (map.has(key))
{
if (map.get(key) != matrix[i][j])
return false;
}
else
{
map.set(i - j, matrix[i][j]);
}
}
}
return true;
}
let matrix = [ [ 12, 23, -32 ],
[ -20, 12, 23 ],
[ 56, -20, 12 ],
[38, 56, -20 ] ];
let result = (isToeplitz(matrix)) ? "Yes" : "No";
document.write(result);
</script>
|
Time Complexity: O(mn), where m is number of rows and n is number of columns.
Auxiliary Space: O(m+n), because at worst case, if a matrix is Toeplitz, we have store exactly (m+n-1) key, value pairs. (In first row we have n distinct keys and then for next each m-1 rows, we keep adding one unique key to the map.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...