Find if a degree sequence can form a simple graph | Havel-Hakimi Algorithm
Last Updated :
25 Aug, 2021
Given a sequence of non-negative integers arr[], the task is to check if there exists a simple graph corresponding to this degree sequence. Note that a simple graph is a graph with no self-loops and parallel edges.
Examples:
Input: arr[] = {3, 3, 3, 3}
Output: Yes
This is actually a complete graph(K4)
Input: arr[] = {3, 2, 1, 0}
Output: No
A vertex has degree n-1 so it’s connected to all the other n-1 vertices.
But another vertex has degree 0 i.e. isolated. It’s a contradiction.
Approach: One way to check the existence of a simple graph is by Havel-Hakimi algorithm given below:
- Sort the sequence of non-negative integers in non-increasing order.
- Delete the first element(say V). Subtract 1 from the next V elements.
- Repeat 1 and 2 until one of the stopping conditions is met.
Stopping conditions:
- All the elements remaining are equal to 0 (Simple graph exists).
- Negative number encounter after subtraction (No simple graph exists).
- Not enough elements remaining for the subtraction step (No simple graph exists).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool graphExists(vector<int> &a, int n)
{
while (1)
{
sort(a.begin(), a.end(), greater<>());
if (a[0] == 0)
return true;
int v = a[0];
a.erase(a.begin() + 0);
if (v > a.size())
return false;
for (int i = 0; i < v; i++)
{
a[i]--;
if (a[i] < 0)
return false;
}
}
}
int main()
{
vector<int> a = {3, 3, 3, 3};
int n = a.size();
graphExists(a, n) ? cout << "Yes" :
cout << "NO" << endl;
return 0;
}
|
Java
import java.util.*;
@SuppressWarnings("unchecked")
class GFG{
static boolean graphExists(ArrayList a, int n)
{
while (true)
{
Collections.sort(a, Collections.reverseOrder());
if ((int)a.get(0) == 0)
return true;
int v = (int)a.get(0);
a.remove(a.get(0));
if (v > a.size())
return false;
for(int i = 0; i < v; i++)
{
a.set(i, (int)a.get(i) - 1);
if ((int)a.get(i) < 0)
return false;
}
}
}
public static void main(String[] args)
{
ArrayList a = new ArrayList();
a.add(3);
a.add(3);
a.add(3);
a.add(3);
int n = a.size();
if (graphExists(a, n))
{
System.out.print("Yes");
}
else
{
System.out.print("NO");
}
}
}
|
Python3
def graphExists(a):
while True:
a = sorted(a, reverse = True)
if a[0]== 0 and a[len(a)-1]== 0:
return True
v = a[0]
a = a[1:]
if v>len(a):
return False
for i in range(v):
a[i]-= 1
if a[i]<0:
return False
a = [3, 3, 3, 3]
if(graphExists(a)):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections;
class GFG{
static bool graphExists(ArrayList a, int n)
{
while (true)
{
a.Sort();
a.Reverse();
if ((int)a[0] == 0)
return true;
int v = (int)a[0];
a.Remove(a[0]);
if (v > a.Count)
return false;
for(int i = 0; i < v; i++)
{
a[i] = (int)a[i] - 1;
if ((int)a[i] < 0)
return false;
}
}
}
public static void Main(string[] args)
{
ArrayList a = new ArrayList(){ 3, 3, 3, 3 };
int n = a.Count;
if (graphExists(a, n))
{
Console.Write("Yes");
}
else
{
Console.Write("NO");
}
}
}
|
Javascript
<script>
function graphExists(a, n)
{
while (1)
{
a.sort((a, b) => b - a)
if (a[0] == 0)
return true;
var v = a[0];
a.shift();
if (v > a.length)
return false;
for(var i = 0; i < v; i++)
{
a[i]--;
if (a[i] < 0)
return false;
}
}
}
var a = [ 3, 3, 3, 3 ];
var n = a.length;
graphExists(a, n) ? document.write("Yes"):
document.write("NO");
</script>
|
Time Complexity: O(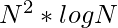 )
)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...