Find Harmonic mean using Arithmetic mean and Geometric mean
Last Updated :
17 Feb, 2023
Given two numbers, first calculate arithmetic mean and geometric mean of these two numbers. Using the arithmetic mean and geometric mean so calculated, find the harmonic mean between the two numbers.
Examples:
Input : a = 2
b = 4
Output : 2.666
Input : a = 5
b = 15
Output : 7.500
Arithmetic Mean: Arithmetic Mean ‘AM’ between two numbers a and b is such a number that AM-a = b-AM. Thus, if we are given these two numbers, the arithmetic mean AM = 1/2(a+b)
Geometric Mean: Geometric Mean ‘GM’ between two numbers a and b is such a number that GM/a = b/GM. Thus, if we are given these two numbers, the geometric mean GM = sqrt(a*b)
Harmonic Mean: Harmonic Mean ‘HM’ between two numbers a and b is such a number that 1/HM – 1/a = 1/b – 1/HM. Thus, if we are given these two numbers, the harmonic mean HM = 2ab/a+b
Now, we also know that 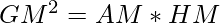
C++
#include <bits/stdc++.h>
using namespace std;
double compute(int a, int b)
{
double AM, GM, HM;
AM = (a + b) / 2;
GM = sqrt(a * b);
HM = (GM * GM) / AM;
return HM;
}
int main()
{
int a = 5, b = 15;
double HM = compute(a, b);
cout << "Harmonic Mean between " << a
<< " and " << b << " is " << HM ;
return 0;
}
|
Java
import java.io.*;
class GeeksforGeeks {
static double compute(int a, int b)
{
double AM, GM, HM;
AM = (a + b) / 2;
GM = Math.sqrt(a * b);
HM = (GM * GM) / AM;
return HM;
}
public static void main(String args[])
{
int a = 5, b = 15;
double HM = compute(a, b);
String str = "";
str = str + HM;
System.out.print("Harmonic Mean between "
+ a + " and " + b + " is "
+ str.substring(0, 5));
}
}
|
Python3
import math
def compute( a, b) :
AM = (a + b) / 2
GM = math.sqrt(a * b)
HM = (GM * GM) / AM
return HM
a = 5
b = 15
HM = compute(a, b)
print("Harmonic Mean between " , a,
" and ", b , " is " , HM )
|
C#
using System;
class GeeksforGeeks {
static double compute(int a, int b)
{
double AM, GM, HM;
AM = (a + b) / 2;
GM = Math.Sqrt(a * b);
HM = (GM * GM) / AM;
return HM;
}
public static void Main()
{
int a = 5, b = 15;
double HM = compute(a, b);
Console.WriteLine("Harmonic Mean between "
+ a + " and " + b + " is "
+HM);
}
}
|
PHP
<?php
function compute( $a, $b)
{
$AM;
$GM;
$HM;
$AM = ($a + $b) / 2;
$GM = sqrt($a * $b);
$HM = ($GM * $GM) / $AM;
return $HM;
}
$a = 5;
$b = 15;
$HM = compute($a, $b);
echo"Harmonic Mean between " .$a.
" and " .$b. " is " .$HM ;
return 0;
?>
|
Javascript
<script>
function compute(a, b)
{
var AM = (a + b) / 2;
var GM = Math.sqrt(a * b);
var HM = (GM * GM) / AM;
return HM;
}
var a = 5;
var b = 15;
var HM = compute(a, b)
document.write("Harmonic Mean between " +
a + " and " + b + " is " +
HM.toFixed(3));
</script>
|
Output:
Harmonic Mean between 5 and 15 is 7.500
Time Complexity: O(log(a*b)), for using sqrt function where a and b represents the given integers.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...