Find four factors of N with maximum product and sum equal to N
Last Updated :
14 Feb, 2023
Given an integer 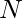 . The task is to find all factors of N print the product of four factors of N such that:
. The task is to find all factors of N print the product of four factors of N such that:
- Sum of the four factors is equal to N.
- Product of the four factors is maximum.
If it is not possible to find 4 such factors then print “Not possible”.
Note: All the four factors can be equal to each other to maximize the product.
Examples:
Input : 24
Output : Product -> 1296
All factors are -> 1 2 3 4 6 8 12 24
Choose the factor 6 four times,
Therefore, 6+6+6+6 = 24 and product is maximum.
Input : 100
Output : Product -> 390625
All the factors are -> 1 2 4 5 10 10 20 25 50 100
Choose the factor 25 four times.
In the second example, the product will be maximum when the four factors will be equal to 25. The sum of four factors is equal to ‘N’. Though we can choose the same factor four times to maximize the product.
Below is the step by step algorithm to solve this problem:
- First find the factors of a number ‘N’ by traversing from 1 to square root of ‘N’ and check if ‘i’ and ‘n/i’ divide N and store them in a vector.
- Sort the vector and print every element.
- Find three numbers to maximize the product with the fourth number, using three loops.
- Replace the next maximum product with the previous product.
- Print the product when you’ll find the four factors.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findfactors(int n)
{
vector<int> vec;
for (int i = 1; i * i <= n; i++) {
if (n % i == 0) {
vec.push_back(i);
vec.push_back(n / i);
}
}
sort(vec.begin(), vec.end());
cout << "All the factors are -> ";
for (int i = 0; i < vec.size(); i++)
cout << vec[i] << " ";
cout << endl;
int maxProduct = 1;
bool flag = 1;
for (int i = 0; i < vec.size(); i++) {
for (int j = i; j < vec.size(); j++) {
for (int k = j; k < vec.size(); k++) {
int y = n - vec[i] - vec[j] - vec[k];
if (y <= 0)
break;
if (n % y == 0) {
flag = 0;
maxProduct = max(vec[i] * vec[j] * vec[k] * y,
maxProduct);
}
}
}
}
if (flag == 0)
cout << "Product is -> " << maxProduct << endl;
else
cout << "Not possible" << endl;
}
int main()
{
int n;
n = 50;
findfactors(n);
return 0;
}
|
Java
import java.util.Collections;
import java.util.Vector;
class GFG
{
static void findfactors(int n)
{
Vector<Integer> vec = new Vector<Integer>();
for (int i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
vec.add(i);
vec.add(n / i);
}
}
Collections.sort(vec);
System.out.println("All the factors are -> ");
for (int i = 0; i < vec.size(); i++)
{
System.out.print(vec.get(i) + " ");
}
System.out.println();
int maxProduct = 1;
boolean flag = true;
for (int i = 0; i < vec.size(); i++)
{
for (int j = i; j < vec.size(); j++)
{
for (int k = j; k < vec.size(); k++)
{
int y = n - vec.get(i) - vec.get(j) -
vec.get(k);
if (y <= 0)
{
break;
}
if (n % y == 0)
{
flag = false;
maxProduct = Math.max(vec.get(i) * vec.get(j) *
vec.get(k) * y, maxProduct);
}
}
}
}
if (flag == false)
{
System.out.println("Product is -> " + maxProduct);
}
else
{
System.out.println("Not possible");
}
}
public static void main(String[] args)
{
int n;
n = 50;
findfactors(n);
}
}
|
Python3
from math import *
def findfactors(n) :
vec = []
for i in range(1, int(sqrt(n)) + 1) :
if n % i == 0 :
vec.append(i)
vec.append(n // i)
vec.sort()
print("All the factors are -> ",
end = "")
for i in range(len(vec)) :
print(vec[i], end = " ")
print()
maxProduct = 1
flag = 1
for i in range(0, len(vec)) :
for j in range(i, len(vec)) :
for k in range(j, len(vec)) :
y = n - vec[i] - vec[j] - vec[k]
if y <= 0 :
break
if n % y == 0 :
flag = 0
maxProduct = max(vec[i] * vec[j] *
vec[k] * y , maxProduct)
if flag == 0 :
print("Product is - >", maxProduct)
else :
print("Not possible")
if __name__ == "__main__" :
n = 50
findfactors(n)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void findfactors(int n)
{
List<int> vec = new List<int>();
for (int i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
vec.Add(i);
vec.Add(n / i);
}
}
vec.Sort();
Console.WriteLine("All the factors are -> ");
for (int i = 0; i < vec.Count; i++)
{
Console.Write(vec[i] + " ");
}
Console.WriteLine();
int maxProduct = 1;
Boolean flag = true;
for (int i = 0; i < vec.Count; i++)
{
for (int j = i; j < vec.Count; j++)
{
for (int k = j; k < vec.Count; k++)
{
int y = n - vec[i] - vec[j] -
vec[k];
if (y <= 0)
{
break;
}
if (n % y == 0)
{
flag = false;
maxProduct = Math.Max(vec[i] * vec[j] *
vec[k] * y, maxProduct);
}
}
}
}
if (flag == false)
{
Console.WriteLine("Product is -> " +
maxProduct);
}
else
{
Console.WriteLine("Not possible");
}
}
public static void Main(String[] args)
{
int n;
n = 50;
findfactors(n);
}
}
|
PHP
<?php
function findfactors($n)
{
$vec = array();
for ($i = 1; $i * $i <= $n; $i++)
{
if ($n % $i == 0)
{
array_push($vec, $i);
array_push($vec, ($n / $i));
}
}
sort($vec);
echo "All the factors are -> ";
for ($i = 0; $i < sizeof($vec); $i++)
echo $vec[$i] . " ";
echo "\n";
$maxProduct = 1;
$flag = 1;
for ($i = 0; $i < sizeof($vec); $i++)
{
for ($j = $i;
$j < sizeof($vec); $j++)
{
for ($k = $j;
$k < sizeof($vec); $k++)
{
$y = $n - $vec[$i] -
$vec[$j] - $vec[$k];
if ($y <= 0)
break;
if ($n % $y == 0)
{
$flag = 0;
$maxProduct = max($vec[$i] * $vec[$j] *
$vec[$k] * $y, $maxProduct);
}
}
}
}
if ($flag == 0)
echo "Product is -> " .
$maxProduct ."\n";
else
echo "Not possible" ."\n";
}
$n = 50;
findfactors($n);
?>
|
Javascript
<script>
function findfactors(n)
{
let vec = [];
for (let i = 1; i * i <= n; i++)
{
if (n % i == 0)
{
vec.push(i);
vec.push(Math.floor(n / i));
}
}
vec.sort(function(a,b){return a-b;});
document.write("All the factors are -> ");
for (let i = 0; i < vec.length; i++)
{
document.write(vec[i] + " ");
}
document.write("<br>");
let maxProduct = 1;
let flag = true;
for (let i = 0; i < vec.length; i++)
{
for (let j = i; j < vec.length; j++)
{
for (let k = j; k < vec.length; k++)
{
let y = n - vec[i] - vec[j] -
vec[k];
if (y <= 0)
{
break;
}
if (n % y == 0)
{
flag = false;
maxProduct = Math.max(vec[i] *
vec[j] * vec[k] * y, maxProduct);
}
}
}
}
if (flag == false)
{
document.write("Product is -> " + maxProduct);
}
else
{
document.write("Not possible");
}
}
let n = 50;
findfactors(n);
</script>
|
Output: All the factors are -> 1 2 5 10 25 50
Product is -> 12500
Time Complexity: O(sqrt(n)+m3) where m is the number of factors of n.
Auxiliary Space: O(m)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...