Find foot of perpendicular from a point in 2 D plane to a Line

Given a point P in 2-D plane and equation of a line, the task is to find the foot of the perpendicular from P to the line.

Note: Equation of line is in form ax+by+c=0.

Examples:

Input :  P=(1, 0), a = -1, b = 1, c = 0
Output : Q = (0.5, 0.5)
The foot of perpendicular from point (1, 0) 
to line -x + y = 0 is (0.5, 0.5)

Input :  P=(3, 3), a = 0, b = 1, c = -2
Output : Q = (3, 2)
The foot of perpendicular from point (3, 3) 
to line y-2 = 0 is (3, 2)

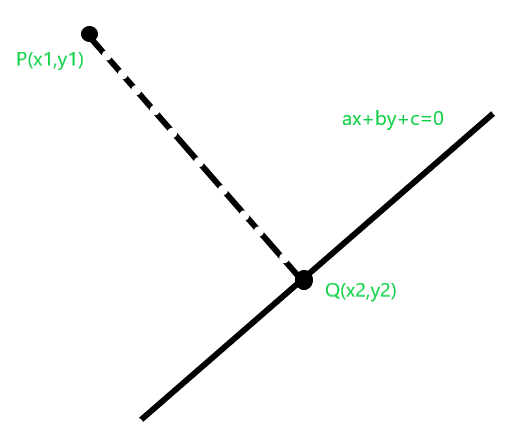
Since equation of the line is given to be of the form ax + by + c = 0. Equation of line passing through P and is perpendicular to line. Therefore equation of line passing through P and Q becomes ay – bx + d = 0. Also, P passes through line passing through P and Q, so we put coordinate of P in the above equation:

ay1 - bx1 + d = 0 
or, d = bx1 - ay1

Also, Q is the intersection of the given line and the line passing through P and Q. So we can find the solution of:

ax + by + c = 0
and,
ay - bx + (bx1-ay1) = 0

Since a, b, c, d all are known we can find x and y here as:

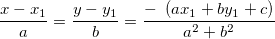
Below is the implementation of the above approach:

C++

// C++ program for implementation of
// the above approach
#include <iostream>
using namespace std;
 
// Function to find foot of perpendicular from
// a point in 2 D plane to a Line
pair<double, double> findFoot(double a, double b, double c,
                              double x1, double y1)
{
    double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
    double x = temp * a + x1;
    double y = temp * b + y1;
    return make_pair(x, y);
}
 
// Driver Code
int main()
{
    // Equation of line is
    // ax + by + c = 0
    double a = 0.0;
    double b = 1.0;
    double c = -2;
 
    // Coordinates of point p(x1, y1).
    double x1 = 3.0;
    double y1 = 3.0;
 
    pair<double, double> foot = findFoot(a, b, c, x1, y1);
    cout << foot.first << " " << foot.second;
 
    return 0;
}

Java

import javafx.util.Pair;
 
// Java program for implementation of
// the above approach
class GFG
{
 
// Function to find foot of perpendicular from
// a point in 2 D plane to a Line
static Pair<Double, Double> findFoot(double a, double b, double c,
                            double x1, double y1)
{
    double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
    double x = temp * a + x1;
    double y = temp * b + y1;
    return new Pair(x, y);
}
 
// Driver Code
public static void main(String[] args)
{
    // Equation of line is
    // ax + by + c = 0
    double a = 0.0;
    double b = 1.0;
    double c = -2;
 
    // Coordinates of point p(x1, y1).
    double x1 = 3.0;
    double y1 = 3.0;
 
    Pair<Double, Double> foot = findFoot(a, b, c, x1, y1);
    System.out.println(foot.getKey() + " " + foot.getValue());
    }
}
 
// This code contributed by Rajput-Ji

Python3

# Python3 implementation of the approach
 
# Function to find foot of perpendicular
# from a point in 2 D plane to a Line
def findFoot(a, b, c, x1, y1):
 
    temp = (-1 * (a * x1 + b * y1 + c) //
                  (a * a + b * b))
    x = temp * a + x1
    y = temp * b + y1
    return (x, y)
 
# Driver Code
if __name__ == "__main__":
 
    # Equation of line is
    # ax + by + c = 0
    a, b, c = 0.0, 1.0, -2
     
    # Coordinates of point p(x1, y1).
    x1, y1 = 3.0, 3.0
 
    foot = findFoot(a, b, c, x1, y1)
    print(int(foot[0]), int(foot[1]))
         
# This code is contributed
# by Rituraj Jain

C#

// C# program for implementation of
// the above approach
using System;
 
class GFG
{
    // Pair class
    public class Pair
    {
        public double first,second;
        public Pair(double a,double b)
        {
            first = a;
            second = b;
        }
    }
 
// Function to find foot of perpendicular from
// a point in 2 D plane to a Line
static Pair findFoot(double a, double b, double c,
                            double x1, double y1)
{
    double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
    double x = temp * a + x1;
    double y = temp * b + y1;
    return new Pair(x, y);
}
 
// Driver Code
public static void Main(String []args)
{
    // Equation of line is
    // ax + by + c = 0
    double a = 0.0;
    double b = 1.0;
    double c = -2;
 
    // Coordinates of point p(x1, y1).
    double x1 = 3.0;
    double y1 = 3.0;
 
    Pair foot = findFoot(a, b, c, x1, y1);
    Console.WriteLine(foot.first + " " + foot.second);
    }
}
 
// This code contributed by Arnab Kundu

PHP

<?php
// PHP implementation of the approach
 
// Function to find foot of perpendicular
// from a point in 2 D plane to a Line
function findFoot($a, $b, $c, $x1, $y1)
{
 
    $temp = floor((-1 * ($a * $x1 + $b * $y1 + $c) /
                        ($a * $a + $b * $b)));
    $x = $temp * $a + $x1;
    $y = $temp * $b + $y1;
    return array($x, $y);
 
}
 
// Driver Code
 
// Equation of line is
// ax + by + c = 0
$a = 0.0;
$b = 1.0 ;
$c = -2 ;
 
// Coordinates of point p(x1, y1).
$x1 = 3.0 ;
$y1 = 3.0 ;
 
$foot = findFoot($a, $b, $c, $x1, $y1);
echo floor($foot[0]), " ", floor($foot[1]);
 
// This code is contributed by Ryuga
?>

Javascript

<script>
      // JavaScript implementation of the approach
 
      // Function to find foot of perpendicular
      // from a point in 2 D plane to a Line
      function findFoot(a, b, c, x1, y1) {
        var temp = (-1 * (a * x1 + b * y1 + c)) / (a * a + b * b);
        var x = temp * a + x1;
        var y = temp * b + y1;
        return [x, y];
      }
 
      // Driver Code
      // Equation of line is
      // ax + by + c = 0
      var a = 0.0;
      var b = 1.0;
      var c = -2;
 
      // Coordinates of point p(x1, y1).
      var x1 = 3.0;
      var y1 = 3.0;
 
      var foot = findFoot(a, b, c, x1, y1);
      document.write(parseInt(foot[0]) + " " + parseInt(foot[1]));
    </script>