Find first node of loop in a linked list
Last Updated :
11 Jan, 2024
Write a function findFirstLoopNode() that checks whether a given Linked List contains a loop. If the loop is present then it returns point to the first node of the loop. Else it returns NULL.
Example :
Input : Head of below linked list
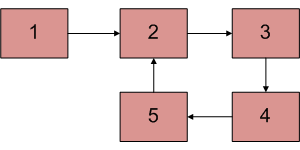
Output : Pointer to node 2
We have discussed Floyd’s loop detection algorithm. Below are steps to find the first node of the loop.
1. If a loop is found, initialize a slow pointer to head, let fast pointer be at its position.
2. Move both slow and fast pointers one node at a time.
3. The point at which they meet is the start of the loop.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* next;
};
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->next = NULL;
return temp;
}
void printList(Node* head)
{
while (head != NULL) {
cout << head->key << " ";
head = head->next;
}
cout << endl;
}
Node* detectAndRemoveLoop(Node* head)
{
if (head == NULL || head->next == NULL)
return NULL;
Node *slow = head, *fast = head;
slow = slow->next;
fast = fast->next->next;
while (fast && fast->next) {
if (slow == fast)
break;
slow = slow->next;
fast = fast->next->next;
}
if (slow != fast)
return NULL;
slow = head;
while (slow != fast) {
slow = slow->next;
fast = fast->next;
}
return slow;
}
int main()
{
Node* head = newNode(50);
head->next = newNode(20);
head->next->next = newNode(15);
head->next->next->next = newNode(4);
head->next->next->next->next = newNode(10);
head->next->next->next->next->next = head->next->next;
Node* res = detectAndRemoveLoop(head);
if (res == NULL)
cout << "Loop does not exist";
else
cout << "Loop starting node is " << res->key;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int key;
struct Node* next;
} Node;
Node* newNode(int key)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->key = key;
temp->next = NULL;
return temp;
}
void printList(Node* head)
{
while (head != NULL) {
printf("%d ",head->key);
head = head->next;
}
printf("/n");
}
Node* detectAndRemoveLoop(Node* head)
{
if (head == NULL || head->next == NULL)
return NULL;
Node *slow = head, *fast = head;
slow = slow->next;
fast = fast->next->next;
while (fast && fast->next) {
if (slow == fast)
break;
slow = slow->next;
fast = fast->next->next;
}
if (slow != fast)
return NULL;
slow = head;
while (slow != fast) {
slow = slow->next;
fast = fast->next;
}
return slow;
}
int main()
{
Node* head = newNode(50);
head->next = newNode(20);
head->next->next = newNode(15);
head->next->next->next = newNode(4);
head->next->next->next->next = newNode(10);
head->next->next->next->next->next = head->next->next;
Node* res = detectAndRemoveLoop(head);
if (res == NULL)
printf("Loop does not exist");
else
printf("Loop starting node is %d ",res->key);
return 0;
}
|
Java
import java.util.*;
class GFG{
static class Node
{
int key;
Node next;
};
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
static void printList(Node head)
{
while (head != null)
{
System.out.print(head.key + " ");
head = head.next;
}
System.out.println();
}
static Node detectAndRemoveLoop(Node head)
{
if (head == null || head.next == null)
return null;
Node slow = head, fast = head;
slow = slow.next;
fast = fast.next.next;
while (fast != null &&
fast.next != null)
{
if (slow == fast)
break;
slow = slow.next;
fast = fast.next.next;
}
if (slow != fast)
return null;
slow = head;
while (slow != fast)
{
slow = slow.next;
fast = fast.next;
}
return slow;
}
public static void main(String[] args)
{
Node head = newNode(50);
head.next = newNode(20);
head.next.next = newNode(15);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next = head.next.next;
Node res = detectAndRemoveLoop(head);
if (res == null)
System.out.print("Loop does not exist");
else
System.out.print("Loop starting node is " + res.key);
}
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.next = None
def newNode(key):
temp = Node(key)
return temp
def printList(head):
while (head != None):
print(head.key, end = ' ')
head = head.next
print()
def detectAndRemoveLoop(head):
if (head == None or head.next == None):
return None
slow = head
fast = head
slow = slow.next
fast = fast.next.next
while (fast and fast.next):
if (slow == fast):
break
slow = slow.next
fast = fast.next.next
if (slow != fast):
return None
slow = head
while (slow != fast):
slow = slow.next
fast = fast.next
return slow
if __name__=='__main__':
head = newNode(50)
head.next = newNode(20)
head.next.next = newNode(15)
head.next.next.next = newNode(4)
head.next.next.next.next = newNode(10)
head.next.next.next.next.next = head.next.next
res = detectAndRemoveLoop(head)
if (res == None):
print("Loop does not exist")
else:
print("Loop starting node is " +
str(res.key))
|
C#
using System;
class GFG{
class Node
{
public int key;
public Node next;
};
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
static void printList(Node head)
{
while (head != null)
{
Console.Write(head.key + " ");
head = head.next;
}
Console.WriteLine();
}
static Node detectAndRemoveLoop(Node head)
{
if (head == null || head.next == null)
return null;
Node slow = head, fast = head;
slow = slow.next;
fast = fast.next.next;
while (fast != null &&
fast.next != null)
{
if (slow == fast)
break;
slow = slow.next;
fast = fast.next.next;
}
if (slow != fast)
return null;
slow = head;
while (slow != fast)
{
slow = slow.next;
fast = fast.next;
}
return slow;
}
public static void Main(String[] args)
{
Node head = newNode(50);
head.next = newNode(20);
head.next.next = newNode(15);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next =
head.next.next;
Node res = detectAndRemoveLoop(head);
if (res == null)
Console.Write("Loop does not exist");
else
Console.Write("Loop starting node is " +
res.key);
}
}
|
Javascript
<script>
class Node
{
constructor(key)
{
this.key=key;
this.next=null;
}
}
function printList(head)
{
while (head != null)
{
document.write(head.key + " ");
head = head.next;
}
document.write("<br>");
}
function detectAndRemoveLoop(head)
{
if (head == null || head.next == null)
return null;
let slow = head, fast = head;
slow = slow.next;
fast = fast.next.next;
while (fast != null &&
fast.next != null)
{
if (slow == fast)
break;
slow = slow.next;
fast = fast.next.next;
}
if (slow != fast)
return null;
slow = head;
while (slow != fast)
{
slow = slow.next;
fast = fast.next;
}
return slow;
}
let head = new Node(50);
head.next = new Node(20);
head.next.next = new Node(15);
head.next.next.next = new Node(4);
head.next.next.next.next = new Node(10);
head.next.next.next.next.next = head.next.next;
let res = detectAndRemoveLoop(head);
if (res == null)
document.write("Loop does not exist");
else
document.write("Loop starting node is " + res.key);
</script>
|
Output
Loop starting node is 15
Time Complexity: O(N), where N is length of array.
Auxiliary Space: O(1)
How does this approach work?
Let slow and fast meet at some point after Floyd’s Cycle finding algorithm. The below diagram shows the situation when the cycle is found.
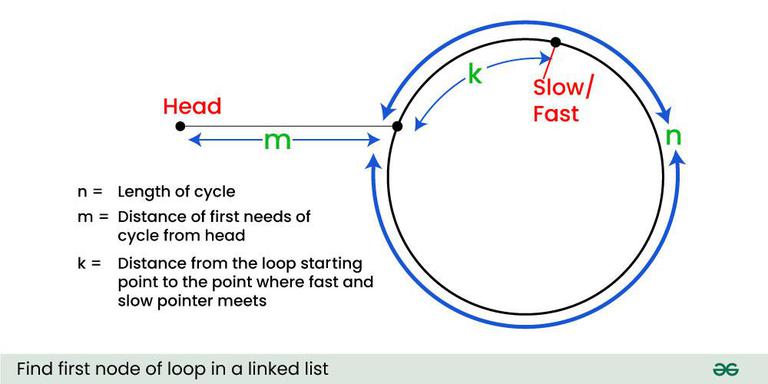
Find first node of loop in a linked list
We can conclude below from the above diagram
Distance traveled by fast pointer = 2 * (Distance traveled
by slow pointer)
(m + n*x + k) = 2*(m + n*y + k)
Note that before meeting the point shown above, fast
was moving at twice speed.
x --> Number of complete cyclic rounds made by
fast pointer before they meet first time
y --> Number of complete cyclic rounds made by
slow pointer before they meet first time
From the above equation, we can conclude below
m + k = (x-2y)*n
Which means m+k is a multiple of n.
So if we start moving both pointers again at the same speed such that one pointer (say slow) begins from the head node of the linked list and other pointers (say fast) begins from the meeting point. When the slow pointer reaches the beginning of the loop (has made m steps), the fast pointer would have made also moved m steps as they are now moving the same pace. Since m+k is a multiple of n and fast starts from k, they would meet at the beginning. Can they meet before also? No, because the slow pointer enters the cycle first time after m steps.
Method 2:
In this method, a temporary node is created. The next pointer of each node that is traversed is made to point to this temporary node. This way we are using the next pointer of a node as a flag to indicate whether the node has been traversed or not. Every node is checked to see if the next is pointing to a temporary node or not. In the case of the first node of the loop, the second time we traverse it this condition will be true, hence we return that node.
The code runs in O(n) time complexity and uses constant memory space.
Steps to solve this problem:
1. Create a temporary node and a pointer temp.
2. While head is not null:
*Check if head->next is null then return null.
*Check if head->next is temp than break.
*Create a nex pointer to a node and point it to head->next.
*Point head->next to temp.
*Update head to nex.
3. Return head.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* next;
};
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->next = NULL;
return temp;
}
void printList(Node* head)
{
while (head != NULL) {
cout << head->key << " ";
head = head->next;
}
cout << endl;
}
Node* detectLoop(Node* head)
{
Node* temp = new Node;
while (head != NULL) {
if (head->next == NULL) {
return NULL;
}
if (head->next == temp) {
break;
}
Node* nex = head->next;
head->next = temp;
head = nex;
}
return head;
}
int main()
{
Node* head = newNode(50);
head->next = newNode(20);
head->next->next = newNode(15);
head->next->next->next = newNode(4);
head->next->next->next->next = newNode(10);
head->next->next->next->next->next = head->next->next;
Node* res = detectLoop(head);
if (res == NULL)
cout << "Loop does not exist";
else
cout << "Loop starting node is " << res->key;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int key;
struct Node* next;
} Node;
Node* newNode(int key)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->key = key;
temp->next = NULL;
return temp;
}
void printList(Node* head)
{
while (head != NULL) {
printf("%d ", head->key);
head = head->next;
}
printf("\n");
}
Node* detectLoop(Node* head)
{
Node* temp = (Node *)malloc(sizeof(Node));
while (head != NULL) {
if (head->next == NULL)
return NULL;
if (head->next == temp)
break;
Node* nex = head->next;
head->next = temp;
head = nex;
}
return head;
}
int main()
{
Node* head = newNode(50);
head->next = newNode(20);
head->next->next = newNode(15);
head->next->next->next = newNode(4);
head->next->next->next->next = newNode(10);
head->next->next->next->next->next = head->next->next;
Node* res = detectLoop(head);
if (res == NULL)
printf("Loop does not exist");
else
printf("Loop starting node is %d ", res->key);
return 0;
}
|
Java
import java.util.*;
class GFG{
static class Node
{
int key;
Node next;
};
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
static void printList(Node head)
{
while (head != null)
{
System.out.print(head.key + " ");
head = head.next;
}
System.out.println();
}
static Node detectLoop(Node head)
{
Node temp = new Node();
while (head != null)
{
if (head.next == null)
{
return null;
}
if (head.next == temp)
{
break;
}
Node nex = head.next;
head.next = temp;
head = nex;
}
return head;
}
public static void main(String[] args)
{
Node head = newNode(50);
head.next = newNode(20);
head.next.next = newNode(15);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next = head.next.next;
Node res = detectLoop(head);
if (res == null)
System.out.print("Loop does not exist");
else
System.out.print("Loop starting node is " +
res.key);
}
}
|
Python3
class Node:
def __init__(self, x):
self.key = x
self.next = None
def printList(head):
while (head != None):
print(head.key, end = " ")
head = head.next
def detectLoop(head):
temp = Node(-1)
while (head != None):
if (head.next == None):
return None
if (head.next == temp):
break
nex = head.next
head.next = temp
head = nex
return head
if __name__ == '__main__':
head = Node(50)
head.next = Node(20)
head.next.next = Node(15)
head.next.next.next = Node(4)
head.next.next.next.next = Node(10)
head.next.next.next.next.next = head.next.next
res = detectLoop(head)
if (res == None):
print("Loop does not exist")
else:
print("Loop starting node is ", res.key)
|
C#
using System;
class GFG{
class Node
{
public int key;
public Node next;
};
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
static void printList(Node head)
{
while (head != null)
{
Console.Write(head.key + " ");
head = head.next;
}
Console.WriteLine();
}
static Node detectLoop(Node head)
{
Node temp = new Node();
while (head != null)
{
if (head.next == null)
{
return null;
}
if (head.next == temp)
{
break;
}
Node nex = head.next;
head.next = temp;
head = nex;
}
return head;
}
public static void Main(String[] args)
{
Node head = newNode(50);
head.next = newNode(20);
head.next.next = newNode(15);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next = head.next.next;
Node res = detectLoop(head);
if (res == null)
Console.Write("Loop does not exist");
else
Console.Write("Loop starting node is " +
res.key);
}
}
|
Javascript
<script>
class Node {
constructor() {
this.key = 0;
this.next = null;
}
}
function newNode(key) {
temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
function printList( head) {
while (head != null) {
document.write(head.key + " ");
head = head.next;
}
document.write("<br/>");
}
function detectLoop( head) {
temp = new Node();
while (head != null) {
if (head.next == null) {
return null;
}
if (head.next == temp) {
break;
}
nex = head.next;
head.next = temp;
head = nex;
}
return head;
}
head = newNode(50);
head.next = newNode(20);
head.next.next = newNode(15);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next = head.next.next;
res = detectLoop(head);
if (res == null)
document.write("Loop does not exist");
else
document.write("Loop starting node is " + res.key);
</script>
|
Output
Loop starting node is 15
Time Complexity: O(N)
Auxiliary Space: O(1)
Method 3:
We can also use the concept of hashing in order to detect the first node of the loop. The idea is simple just iterate over the entire linked list and store node addresses in a set(C++ STL) one by one, while adding the node address into the set check if it already contains that particular node address if not then add node address to set if it is already present in the set then the current node is the first node of the loop.
C++14
#include<bits/stdc++.h>
using namespace std;
struct ListNode{
int val;
ListNode *next;
ListNode(int x){
this->val = x;
this->next = NULL;
}
};
ListNode* detectCycle(ListNode* A){
unordered_set<ListNode*> uset;
ListNode *ptr = A;
while (ptr != NULL) {
if (uset.find(ptr) != uset.end())
return ptr;
else
uset.insert(ptr);
ptr = ptr->next;
}
return NULL;
}
int main(){
ListNode* head = new ListNode(50);
head->next = new ListNode(20);
head->next->next = new ListNode(15);
head->next->next->next = new ListNode(4);
head->next->next->next->next = new ListNode(10);
head->next->next->next->next->next = head->next->next;
ListNode* res = detectCycle(head);
if (res == NULL)
cout << "Loop does not exist";
else
cout << "Loop starting node is " << res->val;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static Node detectCycle(Node A)
{
Set<Node> uset = new HashSet<Node>();
Node = A;
while (ptr != NULL)
{
if(uset.contains(ptr))
{
return ptr;
}
else
{
uset.add(ptr);
}
ptr = ptr.next;
}
return null;
}
}
|
Python3
def detectCycle(A):
uset = set()
ptr = A
while (ptr != None):
if (ptr in uset):
return ptr
else:
uset.add(ptr)
ptr = ptr.next
return None
|
C#
using System.Collections.Generic;
public class GFG
{
class Node
{
public int key;
public Node next;
};
static Node detectCycle(Node A)
{
HashSet<Node> uset = new HashSet<Node>();
Node ptr = A;
while (ptr != null)
{
if(uset.Contains(ptr))
{
return ptr;
}
else
{
uset.Add(ptr);
}
ptr = ptr.next;
}
return null;
}
}
|
Javascript
<script>
function detectCycle(A)
{
let uset = new Set();
let ptr = A;
while (ptr != NULL)
{
if(uset.has(ptr))
{
return ptr;
}
else
{
uset.add(ptr);
}
ptr = ptr.next;
}
return null;
}
</script>
|
Output
Loop starting node is 15
Time Complexity: O(NlogN)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...