Find count of Almost Prime numbers from 1 to N
Last Updated :
20 Aug, 2022
Given a number N. Find number of almost primes from 1 to 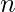 . A number is called almost if it has exactly two distinct prime factors.
. A number is called almost if it has exactly two distinct prime factors.
Note: The numbers can have any number of non-prime factors but should have exactly two prime factors.
Examples:
Input : N = 10
Output : 2
Explanation : 6, 10 are such numbers.
Input : N = 21
Output : 8
An efficient solution is to find prime numbers using Sieve of Eratosthenes. And find distinct prime factors count for numbers less than N.
Please Refer: Almost Prime Numbers
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define N 100005
bool prime[N];
void SieveOfEratosthenes()
{
memset(prime, true, sizeof(prime));
prime[1] = false;
for (int p = 2; p * p < N; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < N; i += p)
prime[i] = false;
}
}
}
int almostPrimes(int n)
{
int ans = 0;
for (int i = 6; i <= n; i++) {
int c = 0;
for (int j = 2; j * j <= i; j++) {
if (i % j == 0) {
if (j * j == i) {
if (prime[j])
c++;
}
else {
if (prime[j])
c++;
if (prime[i / j])
c++;
}
}
}
if (c == 2)
ans++;
}
return ans;
}
int main()
{
SieveOfEratosthenes();
int n = 21;
cout << almostPrimes(n);
return 0;
}
|
C
#include <stdio.h>
#include <stdbool.h>
#include <string.h>
#define N 100005
bool prime[N];
void SieveOfEratosthenes()
{
memset(prime, true, sizeof(prime));
prime[1] = false;
for (int p = 2; p * p < N; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < N; i += p)
prime[i] = false;
}
}
}
int almostPrimes(int n)
{
int ans = 0;
for (int i = 6; i <= n; i++) {
int c = 0;
for (int j = 2; j * j <= i; j++) {
if (i % j == 0) {
if (j * j == i) {
if (prime[j])
c++;
}
else {
if (prime[j])
c++;
if (prime[i / j])
c++;
}
}
}
if (c == 2)
ans++;
}
return ans;
}
int main()
{
SieveOfEratosthenes();
int n = 21;
printf("%d",almostPrimes(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int N = 100005;
static boolean prime[] = new boolean[N];
static void SieveOfEratosthenes()
{
for(int i=0;i<N;i++)
prime[i] =true;
prime[1] = false;
for (int p = 2; p * p < N; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < N; i += p)
prime[i] = false;
}
}
}
static int almostPrimes(int n)
{
int ans = 0;
for (int i = 6; i <= n; i++) {
int c = 0;
for (int j = 2; j * j <= i; j++) {
if (i % j == 0) {
if (j * j == i) {
if (prime[j])
c++;
}
else {
if (prime[j])
c++;
if (prime[i / j])
c++;
}
}
}
if (c == 2)
ans++;
}
return ans;
}
public static void main (String[] args) {
SieveOfEratosthenes();
int n = 21;
System.out.println( almostPrimes(n));
}
}
|
Python 3
from math import *
N = 100005
prime = [True] * N
def SieveOfEratosthenes() :
prime[1] = False
for p in range(2, int(sqrt(N))) :
if prime[p] == True :
for i in range(2*p, N, p) :
prime[i] = False
def almostPrimes(n) :
ans = 0
for i in range(6, n + 1) :
c = 0
for j in range(2, int(sqrt(i)) + 1) :
if i % j == 0 :
if j * j == i :
if prime[j] :
c += 1
else :
if prime[j] :
c += 1
if prime[i // j] :
c += 1
if c == 2 :
ans += 1
return ans
if __name__ == "__main__" :
SieveOfEratosthenes()
n = 21
print(almostPrimes(n))
|
C#
using System;
class GFG
{
static int N = 100005;
static bool []prime = new bool[N];
static void SieveOfEratosthenes()
{
for(int i = 0; i < N; i++)
prime[i] = true;
prime[1] = false;
for (int p = 2; p * p < N; p++)
{
if (prime[p] == true)
{
for (int i = p * 2; i < N; i += p)
prime[i] = false;
}
}
}
static int almostPrimes(int n)
{
int ans = 0;
for (int i = 6; i <= n; i++)
{
int c = 0;
for (int j = 2; j * j <= i; j++)
{
if (i % j == 0)
{
if (j * j == i)
{
if (prime[j])
c++;
}
else
{
if (prime[j])
c++;
if (prime[i / j])
c++;
}
}
}
if (c == 2)
ans++;
}
return ans;
}
public static void Main ()
{
SieveOfEratosthenes();
int n = 21;
Console.WriteLine( almostPrimes(n));
}
}
|
PHP
<?php
$N = 100005;
$prime = array_fill(0, $N, true);
function SieveOfEratosthenes()
{
global $N, $prime;
$prime[1] = false;
for($p = 2; $p < (int)(sqrt($N)); $p++)
{
if ($prime[$p] == true)
for($i = 2 * $p; $i < $N; $i += $p)
$prime[$i] = false;
}
}
function almostPrimes($n)
{
global $prime;
$ans = 0;
for($i = 6; $i < $n + 1; $i++)
{
$c = 0;
for($j = 2; $i >= $j * $j; $j++)
{
if ($i % $j == 0)
{
if ($j * $j == $i)
{
if ($prime[$j])
$c += 1;
}
else
{
if ($prime[$j])
$c += 1;
if ($prime[($i / $j)])
$c += 1;
}
}
}
if ($c == 2)
$ans += 1;
}
return $ans;
}
SieveOfEratosthenes();
$n = 21;
print(almostPrimes($n));
?>
|
Javascript
<script>
let N = 100005;
let prime = new Array(N).fill(true);
function SieveOfEratosthenes()
{
prime[1] = false;
for(let p = 2; p < Math.floor(Math.sqrt(N)); p++)
{
if (prime[p] == true)
for(let i = 2 * p; i < N; i += p)
prime[i] = false;
}
}
function almostPrimes(n)
{
let ans = 0;
for(let i = 6; i < n + 1; i++)
{
let c = 0;
for(let j = 2; i >= j * j; j++)
{
if (i % j == 0)
{
if (j * j == i)
{
if (prime[j])
c += 1;
}
else
{
if (prime[j])
c += 1;
if (prime[(i / j)])
c += 1;
}
}
}
if (c == 2)
ans += 1;
}
return ans;
}
SieveOfEratosthenes();
let n = 21;
document.write(almostPrimes(n));
</script>
|
Time Complexity: O(n3/2 + 1000053/2)
Auxiliary Space: O(100005)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...