Find array using different XORs of elements in groups of size 4
Last Updated :
27 Apr, 2021
Given an array q[] of XOR queries of size N (N is a multiple of 4) which describe an array of the same size as follows:
q[0 – 3] describe arr[0 – 3], q[4 – 7] describe arr[4 – 7], and so on…
If arr[0 – 3] = {a1, a2, a3, a4} then
q[0 – 3] = {a1 ? a2 ? a3, a1 ? a2 ? a4, a1 ? a3 ? a4, a2 ? a3 ? a4}
The task is to find the values of the original array arr[] when only q[] is given.
Example:
Input: q[] = {4, 1, 7, 0}
Output: 2 5 3 6
a1 ? a2 ? a3 = 4 ? 1 ? 7 = 2
a1 ? a2 ? a4 = 4 ? 1 ? 0 = 5
a1 ? a3 ? a4 = 4 ? 7 ? 0 = 3
a2 ? a3 ? a4 = 1 ? 7 ? 0 = 6
Input: q[] = {4, 1, 7, 0, 8, 5, 1, 4}
Output: 2 5 3 6 12 9 13 0
Approach: From the properties of xor, a ? a = 0 and a ? 0 = a.
(a ? b ? c) ? (b ? c ? d) = a ? d (As (b ? c) ? (b ? c) = 0)
So we will divide array in groups of 4 elements and for each group(a, b, c, d) we will
be given results of the following queries:
- a ? b ? c
- a ? b ? d
- a ? c ? d
- b ? c ? d
As (a ? b ? c) ? (b ? c ? d) = a ? d,
using this (a ? d) we can get b and c from query 2 and 3 in the following manner:
(a ? b ? d) ? (a ? d) = b
(a ? c ? d) ? (a ? d) = c
Then using b and c we can get a from query 1 and d from query 4 in the following way:
(a ? b ? c) ? (b) ? (c) = a
(b ? c ? d) ? (b) ? (c) = d
This process will be repeated (iteratively) for all groups of 4 elements and we will get elements of all indices(ex.(a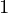 , a
, a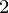 , a
, a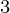 , a
, a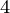 ) then (a
) then (a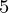 , a
, a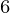 , a
, a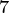 , a
, a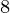 ) etc.)
) etc.)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printArray(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
void findArray(int q[], int n)
{
int arr[n], ans;
for (int k = 0, j = 0; j < n / 4; j++) {
ans = q[k] ^ q[k + 3];
arr[k + 1] = q[k + 1] ^ ans;
arr[k + 2] = q[k + 2] ^ ans;
arr[k] = q[k] ^ ((arr[k + 1]) ^ (arr[k + 2]));
arr[k + 3] = q[k + 3] ^ (arr[k + 1] ^ arr[k + 2]);
k += 4;
}
printArray(arr, n);
}
int main()
{
int q[] = { 4, 1, 7, 0 };
int n = sizeof(q) / sizeof(q[0]);
findArray(q, n);
return 0;
}
|
Java
class GFG
{
static void printArray(int []arr, int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
static void findArray(int []q, int n)
{
int ans;
int []arr = new int[n];
for (int k = 0, j = 0;
j < n / 4; j++)
{
ans = q[k] ^ q[k + 3];
arr[k + 1] = q[k + 1] ^ ans;
arr[k + 2] = q[k + 2] ^ ans;
arr[k] = q[k] ^ ((arr[k + 1]) ^
(arr[k + 2]));
arr[k + 3] = q[k + 3] ^ (arr[k + 1] ^
arr[k + 2]);
k += 4;
}
printArray(arr, n);
}
public static void main(String args[])
{
int []q = { 4, 1, 7, 0 };
int n = q.length;
findArray(q, n);
}
}
|
Python3
def printArray(arr, n):
for i in range(n):
print(arr[i], end = " ")
def findArray(q, n):
arr = [None] * n
k = 0
for j in range(int(n / 4)):
ans = q[k] ^ q[k + 3]
arr[k + 1] = q[k + 1] ^ ans
arr[k + 2] = q[k + 2] ^ ans
arr[k] = q[k] ^ ((arr[k + 1]) ^
(arr[k + 2]))
arr[k + 3] = q[k + 3] ^ (arr[k + 1] ^
arr[k + 2])
k += 4
printArray(arr, n)
if __name__ == '__main__':
q = [4, 1, 7, 0]
n = len(q)
findArray(q, n)
|
C#
using System;
class GFG
{
static void printArray(int []arr, int n)
{
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
static void findArray(int []q, int n)
{
int ans;
int []arr = new int[n] ;
for (int k = 0, j = 0; j < n / 4; j++)
{
ans = q[k] ^ q[k + 3];
arr[k + 1] = q[k + 1] ^ ans;
arr[k + 2] = q[k + 2] ^ ans;
arr[k] = q[k] ^ ((arr[k + 1]) ^ (arr[k + 2]));
arr[k + 3] = q[k + 3] ^ (arr[k + 1] ^ arr[k + 2]);
k += 4;
}
printArray(arr, n);
}
public static void Main()
{
int []q = { 4, 1, 7, 0 };
int n = q.Length ;
findArray(q, n);
}
}
|
PHP
<?php
function printArray($arr, $n)
{
for ($i = 0; $i < $n; $i++)
echo($arr[$i] ." ");
}
function findArray($q, $n)
{
$ans;
$arr = array($n);
for ($k = 0, $j = 0; $j < $n / 4; $j++)
{
$ans = $q[$k] ^ $q[$k + 3];
$arr[$k + 1] = $q[$k + 1] ^ $ans;
$arr[$k + 2] = $q[$k + 2] ^ $ans;
$arr[$k] = $q[$k] ^ (($arr[$k + 1]) ^
($arr[$k + 2]));
$arr[$k + 3] = $q[$k + 3] ^ ($arr[$k + 1] ^
$arr[$k + 2]);
$k += 4;
}
printArray($arr, $n);
}
{
$q = array( 4, 1, 7, 0 );
$n = sizeof($q);
findArray($q, $n);
}
|
Javascript
<script>
function printArray(arr, n)
{
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
}
function findArray(q, n)
{
let arr = new Array(n), ans;
for (let k = 0, j = 0; j <
parseInt(n / 4); j++)
{
ans = q[k] ^ q[k + 3];
arr[k + 1] = q[k + 1] ^ ans;
arr[k + 2] = q[k + 2] ^ ans;
arr[k] = q[k] ^ ((arr[k + 1]) ^
(arr[k + 2]));
arr[k + 3] = q[k + 3] ^ (arr[k + 1] ^
arr[k + 2]);
k += 4;
}
printArray(arr, n);
}
let q = [ 4, 1, 7, 0 ];
let n = q.length;
findArray(q, n);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...