Find if an array of strings can be chained to form a circle | Set 2

Given an array of strings, find if the given strings can be chained to form a circle. A string X can be put before another string Y in a circle if the last character of X is the same as the first character of Y.

Examples: 

Input: arr[] = {"geek", "king"}
Output: Yes, the given strings can be chained.
Note that the last character of first string is same
as first character of second string and vice versa is
also true.

Input: arr[] = {"for", "geek", "rig", "kaf"}
Output: Yes, the given strings can be chained.
The strings can be chained as "for", "rig", "geek" 
and "kaf"

Input: arr[] = {"aab", "bac", "aaa", "cda"}
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bac" 
and "cda"

Input: arr[] = {"aaa", "bbb", "baa", "aab"};
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bbb" 
and "baa"

Input: arr[] = {"aaa"};
Output: Yes

Input: arr[] = {"aaa", "bbb"};
Output: No

Input  : arr[] = ["abc", "efg", "cde", "ghi", "ija"]
Output : Yes
These strings can be reordered as, “abc”, “cde”, “efg”,
“ghi”, “ija”

Input : arr[] = [“ijk”, “kji”, “abc”, “cba”]
Output : No

We strongly recommend that you click here and practice it, before moving on to the solution.

We have discussed one approach to this problem in the below post. 
Find if an array of strings can be chained to form a circle | Set 1

In this post, another approach is discussed. We solve this problem by treating this as a graph problem, where vertices will be the first and last character of strings, and we will draw an edge between two vertices if they are the first and last character of the same string, so a number of edges in the graph will be same as the number of strings in the array. 
Graph representation of some string arrays are given in the below diagram, 

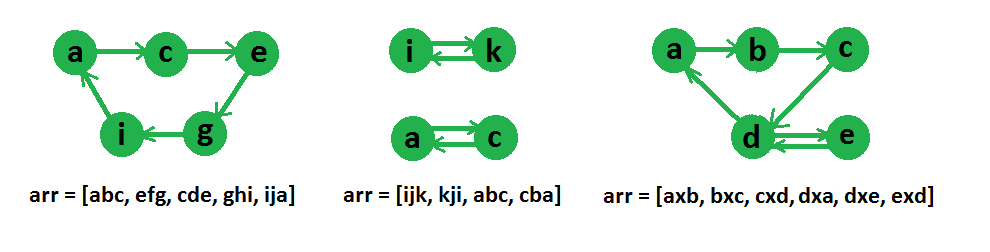
Now it can be clearly seen after graph representation that if a loop among graph vertices is possible then we can reorder the strings otherwise not. As in the above diagram’s example, a loop can be found in the first and third array of string but not in the second array of string. Now to check whether this graph can have a loop which goes through all the vertices, we’ll check two conditions, 

1. Indegree and Outdegree of each vertex should be the same.
2. The graph should be strongly connected.

The first condition can be checked easily by keeping two arrays, in and out for each character. For checking whether a graph is having a loop which goes through all vertices is the same as checking complete directed graph is strongly connected or not because if it has a loop which goes through all vertices then we can reach to any vertex from any other vertex that is, the graph will be strongly connected and the same argument can be given for reverse statement also. 

Now for checking the second condition we will just run a DFS from any character and visit all reachable vertices from this, now if the graph has a loop then after this one DFS all vertices should be visited, if all vertices are visited then we will return true otherwise false so visiting all vertices in a single DFS flags a possible ordering among strings. 

C++

// C++ code to check if cyclic order is possible among strings
// under given constraints
#include <bits/stdc++.h>
using namespace std;
#define M 26

//    Utility method for a depth first search among vertices
void dfs(vector<int> g[], int u, vector<bool> &visit)
{
    visit[u] = true;
    for (int i = 0; i < g[u].size(); ++i)
        if(!visit[g[u][i]])
            dfs(g, g[u][i], visit);
}

//    Returns true if all vertices are strongly connected
// i.e. can be made as loop
bool isConnected(vector<int> g[], vector<bool> &mark, int s)
{
    // Initialize all vertices as not visited
    vector<bool> visit(M, false);

    //    perform a dfs from s
    dfs(g, s, visit);

    //    now loop through all characters
    for (int i = 0; i < M; i++)
    {
        /*  I character is marked (i.e. it was first or last
            character of some string) then it should be
            visited in last dfs (as for looping, graph
            should be strongly connected) */
        if (mark[i] && !visit[i])
            return false;
    }

    //    If we reach that means graph is connected
    return true;
}

//    return true if an order among strings is possible
bool possibleOrderAmongString(string arr[], int N)
{
    // Create an empty graph
    vector<int> g[M];

    // Initialize all vertices as not marked
    vector<bool> mark(M, false);

    // Initialize indegree and outdegree of every
    // vertex as 0.
    vector<int> in(M, 0), out(M, 0);

    // Process all strings one by one
    for (int i = 0; i < N; i++)
    {
        // Find first and last characters
        int f = arr[i].front() - 'a';
        int l = arr[i].back() - 'a';

        // Mark the characters
        mark[f] = mark[l] = true;

        //    increase indegree and outdegree count
        in[l]++;
        out[f]++;

        // Add an edge in graph
        g[f].push_back(l);
    }

    // If for any character indegree is not equal to
    // outdegree then ordering is not possible
    for (int i = 0; i < M; i++)
        if (in[i] != out[i])
            return false;

    return isConnected(g, mark, arr[0].front() - 'a');
}

//    Driver code to test above methods
int main()
{
    // string arr[] = {"abc", "efg", "cde", "ghi", "ija"};
    string arr[] = {"ab", "bc", "cd", "de", "ed", "da"};
    int N = sizeof(arr) / sizeof(arr[0]);

    if (possibleOrderAmongString(arr, N) == false)
        cout << "Ordering not possible\n";
    else
        cout << "Ordering is possible\n";
    return 0;
}

Java

// Java code to check if cyclic order is
// possible among strings under given constraints
import java.io.*;
import java.util.*;

class GFG{

// Return true if an order among strings is possible
public static boolean possibleOrderAmongString(
    String s[], int n)
{
    int m = 26;
    boolean mark[] = new boolean[m];
    int in[] = new int[26];
    int out[] = new int[26];

    ArrayList<
    ArrayList<Integer>> adj = new ArrayList<
                                  ArrayList<Integer>>();
    for(int i = 0; i < m; i++)
        adj.add(new ArrayList<>());

    // Process all strings one by one
    for(int i = 0; i < n; i++)
    {

        // Find first and last characters
        int f = (int)(s[i].charAt(0) - 'a');
        int l = (int)(s[i].charAt(
                 s[i].length() - 1) - 'a');

        // Mark the characters
        mark[f] = mark[l] = true;

        // Increase indegree and outdegree count
        in[l]++;
        out[f]++;

        // Add an edge in graph
        adj.get(f).add(l);
    }

    // If for any character indegree is not equal to
    // outdegree then ordering is not possible
    for(int i = 0; i < m; i++)
    {
        if (in[i] != out[i])
            return false;
    }
    return isConnected(adj, mark,
                       s[0].charAt(0) - 'a');
}

// Returns true if all vertices are strongly
// connected i.e. can be made as loop
public static boolean isConnected(
    ArrayList<ArrayList<Integer>> adj,
    boolean mark[], int src)
{
    boolean visited[] = new boolean[26];

    // Perform a dfs from src
    dfs(adj, visited, src);
    for(int i = 0; i < 26; i++)
    {

        /*  I character is marked (i.e. it was first or
         last character of some string) then it should
         be visited in last dfs (as for looping, graph
         should be strongly connected) */
        if (mark[i] && !visited[i])
            return false;
    }

    // If we reach that means graph is connected
    return true;
}

// Utility method for a depth first
// search among vertices
public static void dfs(ArrayList<ArrayList<Integer>> adj,
                       boolean visited[], int src)
{
    visited[src] = true;
    for(int i = 0; i < adj.get(src).size(); i++)
        if (!visited[adj.get(src).get(i)])
            dfs(adj, visited, adj.get(src).get(i));
}

// Driver code
public static void main(String[] args)
{
    String s[] = { "ab", "bc", "cd", "de", "ed", "da" };
    int n = s.length;

    if (possibleOrderAmongString(s, n))
        System.out.println("Ordering is possible");
    else
        System.out.println("Ordering is not possible");
}
}

// This code is contributed by parascoding

Python3

# Python3 code to check if
# cyclic order is possible
# among strings under given
# constraints
M = 26

# Utility method for a depth
# first search among vertices
def dfs(g, u, visit):
    visit[u] = True

    for i in range(len(g[u])):
        if(not visit[g[u][i]]):
            dfs(g, g[u][i], visit)

# Returns true if all vertices
# are strongly connected i.e.
# can be made as loop
def isConnected(g, mark, s):

    # Initialize all vertices
    # as not visited
    visit = [False for i in range(M)]

    # Perform a dfs from s
    dfs(g, s, visit)

    # Now loop through
    # all characters
    for i in range(M):

        # I character is marked
        # (i.e. it was first or last
        # character of some string)
        # then it should be visited
        # in last dfs (as for looping,
        # graph should be strongly
        # connected) */
        if(mark[i] and (not visit[i])):
            return False

    # If we reach that means
    # graph is connected
    return True

# return true if an order among
# strings is possible
def possibleOrderAmongString(arr, N):

    # Create an empty graph
    g = {}

    # Initialize all vertices
    # as not marked
    mark = [False for i in range(M)]

    # Initialize indegree and
    # outdegree of every
    # vertex as 0.
    In = [0 for i in range(M)]
    out = [0 for i in range(M)]

    # Process all strings
    # one by one
    for i in range(N):

        # Find first and last
        # characters
        f = (ord(arr[i][0]) -
             ord('a'))
        l = (ord(arr[i][-1]) -
             ord('a'))

        # Mark the characters
        mark[f] = True
        mark[l] = True

        # Increase indegree
        # and outdegree count
        In[l] += 1
        out[f] += 1

        if f not in g:
            g[f] = []

        # Add an edge in graph
        g[f].append(l)

    # If for any character
    # indegree is not equal to
    # outdegree then ordering
    # is not possible
    for i in range(M):
        if(In[i] != out[i]):
            return False

    return isConnected(g, mark,
                       ord(arr[0][0]) -
                       ord('a'))

# Driver code
arr = ["ab", "bc",
       "cd", "de",
       "ed", "da"]
N = len(arr)
if(possibleOrderAmongString(arr, N) ==
   False):
    print("Ordering not possible")
else:
    print("Ordering is possible")

# This code is contributed by avanitrachhadiya2155

C#

// C# code to check if cyclic order is
// possible among strings under given constraints
using System;
using System.Collections.Generic;
class GFG {

    // Return true if an order among strings is possible
    static bool possibleOrderAmongString(string[] s, int n)
    {
        int m = 26;
        bool[] mark = new bool[m];
        int[] In = new int[26];
        int[] Out = new int[26];

        List<List<int>> adj = new List<List<int>>();
        for(int i = 0; i < m; i++)
            adj.Add(new List<int>());

        // Process all strings one by one
        for(int i = 0; i < n; i++)
        {

            // Find first and last characters
            int f = (int)(s[i][0] - 'a');
            int l = (int)(s[i][s[i].Length - 1] - 'a');

            // Mark the characters
            mark[f] = mark[l] = true;

            // Increase indegree and outdegree count
            In[l]++;
            Out[f]++;

            // Add an edge in graph
            adj[f].Add(l);
        }

        // If for any character indegree is not equal to
        // outdegree then ordering is not possible
        for(int i = 0; i < m; i++)
        {
            if (In[i] != Out[i])
                return false;
        }
        return isConnected(adj, mark,
                           s[0][0] - 'a');
    }

    // Returns true if all vertices are strongly
    // connected i.e. can be made as loop
    public static bool isConnected(
        List<List<int>> adj,
        bool[] mark, int src)
    {
        bool[] visited = new bool[26];

        // Perform a dfs from src
        dfs(adj, visited, src);
        for(int i = 0; i < 26; i++)
        {

            /*  I character is marked (i.e. it was first or
             last character of some string) then it should
             be visited in last dfs (as for looping, graph
             should be strongly connected) */
            if (mark[i] && !visited[i])
                return false;
        }

        // If we reach that means graph is connected
        return true;
    }

    // Utility method for a depth first
    // search among vertices
    public static void dfs(List<List<int>> adj,
                           bool[] visited, int src)
    {
        visited[src] = true;
        for(int i = 0; i < adj[src].Count; i++)
            if (!visited[adj[src][i]])
                dfs(adj, visited, adj[src][i]);
    }

  static void Main() {
    string[] s = { "ab", "bc", "cd", "de", "ed", "da" };
    int n = s.Length;

    if (possibleOrderAmongString(s, n))
        Console.Write("Ordering is possible");
    else
        Console.Write("Ordering is not possible");
  }
}

// This code is contributed by divyesh072019.

Javascript

<script>
    // Javascript code to check if cyclic order is
    // possible among strings under given constraints

    // Return true if an order among strings is possible
    function possibleOrderAmongString(s, n)
    {
        let m = 26;
        let mark = new Array(m);
        mark.fill(false);
        let In = new Array(26);
        In.fill(0);
        let Out = new Array(26);
        Out.fill(0);

        let adj = [];
        for(let i = 0; i < m; i++)
            adj.push([]);

        // Process all strings one by one
        for(let i = 0; i < n; i++)
        {

            // Find first and last characters
            let f = (s[i][0].charCodeAt() - 'a'.charCodeAt());
            let l = (s[i][s[i].length - 1].charCodeAt() - 'a'.charCodeAt());

            // Mark the characters
            mark[f] = mark[l] = true;

            // Increase indegree and outdegree count
            In[l]++;
            Out[f]++;

            // Add an edge in graph
            adj[f].push(l);
        }

        // If for any character indegree is not equal to
        // outdegree then ordering is not possible
        for(let i = 0; i < m; i++)
        {
            if (In[i] != Out[i])
                return false;
        }
        return isConnected(adj, mark, s[0][0].charCodeAt() - 'a'.charCodeAt());
    }

    // Returns true if all vertices are strongly
    // connected i.e. can be made as loop
    function isConnected(adj, mark, src)
    {
        let visited = new Array(26);
        visited.fill(false);

        // Perform a dfs from src
        dfs(adj, visited, src);
        for(let i = 0; i < 26; i++)
        {

            /*  I character is marked (i.e. it was first or
             last character of some string) then it should
             be visited in last dfs (as for looping, graph
             should be strongly connected) */
            if (mark[i] && !visited[i])
                return false;
        }

        // If we reach that means graph is connected
        return true;
    }

    // Utility method for a depth first
    // search among vertices
    function dfs(adj, visited, src)
    {
        visited[src] = true;
        for(let i = 0; i < adj[src].length; i++)
            if (!visited[adj[src][i]])
                dfs(adj, visited, adj[src][i]);
    }

    let s = [ "ab", "bc", "cd", "de", "ed", "da" ];
    let n = s.length;

    if (possibleOrderAmongString(s, n))
        document.write("Ordering is possible");
    else
        document.write("Ordering is not possible");

    // This code is contributed by decode2207.
</script>

Output

Ordering is possible

Time complexity: O(n)
Auxiliary Space: O(n)

This article is contributed by Utkarsh Trivedi. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.