Find all even length binary sequences with same sum of first and second half bits

Given a number n, find all binary sequences of length 2n such that sum of first n bits is same as sum of last n bits.
Examples: 

Input:  N = 2
Output: 
0101 1111 1001 0110 0000 1010 

Input:  N = 3
Output:  
011011 001001 011101 010001 101011 111111
110011 101101 100001 110101 001010 011110 
010010 001100 000000 010100 101110 100010 
110110 100100 

The idea is to fix first and last bits and then recur for remaining 2*(n-1) bits. There are four possibilities when we fix first and last bits –

1. First and last bits are 1, remaining n – 1 bits on both sides should also have the same sum.
2. First and last bits are 0, remaining n – 1 bits on both sides should also have the same sum.
3. First bit is 1 and last bit is 0, sum of remaining n – 1 bits on left side should be 1 less than the sum n-1 bits on right side.
4. First bit is 0 and last bit is 1, sum of remaining n – 1 bits on left side should be 1 more than the sum n-1 bits on right side.

Below is implementation of above idea –

C++

// C++ program to print even length binary sequences
// whose sum of first and second half bits is same
#include <bits/stdc++.h>
using namespace std;

// Function to print even length binary sequences
// whose sum of first and second half bits is same

// diff --> difference between sums of first n bits
// and last n bits
// out --> output array
// start --> starting index
// end --> ending index
void findAllSequences(int diff, char* out, int start, int end)
{
    // We can't cover difference of more than n with 2n bits
    if (abs(diff) > (end - start + 1) / 2)
        return;

    // if all bits are filled
    if (start > end)
    {
        // if sum of first n bits and last n bits are same
        if (diff == 0)
            cout << out << " ";
        return;
    }

    // fill first bit as 0 and last bit as 1
    out[start] = '0', out[end] = '1';
    findAllSequences(diff + 1, out, start + 1, end - 1);

    // fill first and last bits as 1
    out[start] = out[end] = '1';
    findAllSequences(diff, out, start + 1, end - 1);

    // fill first and last bits as 0
    out[start] = out[end] = '0';
    findAllSequences(diff, out, start + 1, end - 1);

    // fill first bit as 1 and last bit as 0
    out[start] = '1', out[end] = '0';
    findAllSequences(diff - 1, out, start + 1, end - 1);
}

// Driver program
int main()
{
    // input number
    int n = 2;

    // allocate string containing 2*n characters
    char out[2 * n + 1];

    // null terminate output array
    out[2 * n] = '\0';

    findAllSequences(0, out, 0, 2*n - 1);

    return 0;
}

Java

// Java program to print even length binary
// sequences whose sum of first and second
// half bits is same
import java.io.*;
import java.util.*;

class GFG
{
    // Function to print even length binary sequences
    // whose sum of first and second half bits is same

    // diff --> difference between sums of first n bits
    // and last n bits
    // out --> output array
    // start --> starting index
    // end --> ending index
    static void findAllSequences(int diff, char out[],
                                     int start, int end)
    {
        // We can't cover difference of more
        // than n with 2n bits
        if (Math.abs(diff) > (end - start + 1) / 2)
            return;

        // if all bits are filled
        if (start > end)
        {
            // if sum of first n bits and
            // last n bits are same
            if (diff == 0)
            {
                System.out.print(out);
                System.out.print(" ");
            }
            return;
        }

        // fill first bit as 0 and last bit as 1
        out[start] = '0';
        out[end] = '1';
        findAllSequences(diff + 1, out, start + 1, end - 1);

        // fill first and last bits as 1
        out[start] = out[end] = '1';
        findAllSequences(diff, out, start + 1, end - 1);

        // fill first and last bits as 0
        out[start] = out[end] = '0';
        findAllSequences(diff, out, start + 1, end - 1);

        // fill first bit as 1 and last bit as 0
        out[start] = '1';
        out[end] = '0';
        findAllSequences(diff - 1, out, start + 1, end - 1);
    }

    // Driver program
    public static void main (String[] args)
    {
        // input number
        int n = 2;

        // allocate string containing 2*n characters
        char[] out = new char[2 * n + 1];

        // null terminate output array
        out[2 * n] = '\0';

        findAllSequences(0, out, 0, 2*n - 1);
    }
}

// This code is contributed by Pramod Kumar

Python3

# Python3 program to print even length binary sequences
# whose sum of first and second half bits is same

# Function to print even length binary sequences
# whose sum of first and second half bits is same

# diff --> difference between sums of first n bits
# and last n bits
# out --> output array
# start --> starting index
# end --> ending index
def findAllSequences(diff, out, start, end):

    # We can't cover difference of more than n with 2n bits
    if (abs(diff) > (end - start + 1) // 2):
        return;

    # if all bits are filled
    if (start > end):
        # if sum of first n bits and last n bits are same
        if (diff == 0):
            print(''.join(list(out)),end=" ");
        return;

    # fill first bit as 0 and last bit as 1
    out[start] = '0';
    out[end] = '1';
    findAllSequences(diff + 1, out, start + 1, end - 1);

    # fill first and last bits as 1
    out[start] = out[end] = '1';
    findAllSequences(diff, out, start + 1, end - 1);

    # fill first and last bits as 0
    out[start] = out[end] = '0';
    findAllSequences(diff, out, start + 1, end - 1);

    # fill first bit as 1 and last bit as 0
    out[start] = '1';
    out[end] = '0';
    findAllSequences(diff - 1, out, start + 1, end - 1);

# Driver program

# input number
n = 2;

# allocate string containing 2*n characters
out=[""]*(2*n);

findAllSequences(0, out, 0, 2*n - 1);

# This code is contributed by mits

C#

// C# program to print even length binary
// sequences whose sum of first and second
// half bits is same
using System;

class GFG {

    // Function to print even length binary
    // sequences whose sum of first and
    // second half bits is same

    // diff --> difference between sums of
    // first n bits
    // and last n bits
    // out --> output array
    // start --> starting index
    // end --> ending index
    static void findAllSequences(int diff,
            char []outt, int start, int end)
    {

        // We can't cover difference of
        // more than n with 2n bits
        if (Math.Abs(diff) > (end - start
                                   + 1) / 2)
            return;

        // if all bits are filled
        if (start > end)
        {

            // if sum of first n bits and
            // last n bits are same
            if (diff == 0)
            {
                Console.Write(outt);
                Console.Write(" ");
            }
            return;
        }

        // fill first bit as 0 and last bit
        // as 1
        outt[start] = '0';
        outt[end] = '1';
        findAllSequences(diff + 1, outt,
                        start + 1, end - 1);

        // fill first and last bits as 1
        outt[start] = outt[end] = '1';
        findAllSequences(diff, outt,
                        start + 1, end - 1);

        // fill first and last bits as 0
        outt[start] = outt[end] = '0';
        findAllSequences(diff, outt,
                         start + 1, end - 1);

        // fill first bit as 1 and last
        // bit as 0
        outt[start] = '1';
        outt[end] = '0';
        findAllSequences(diff - 1, outt,
                         start + 1, end - 1);
    }

    // Driver program
    public static void Main ()
    {

        // input number
        int n = 2;

        // allocate string containing 2*n
        // characters
        char []outt = new char[2 * n + 1];

        // null terminate output array
        outt[2 * n] = '\0';

        findAllSequences(0, outt, 0, 2*n - 1);
    }
}

// This code is contributed by nitin mittal.

PHP

<?php
// PHP program to print even length binary sequences
// whose sum of first and second half bits is same

// Function to print even length binary sequences
// whose sum of first and second half bits is same

// diff --> difference between sums of first n bits
// and last n bits
// out --> output array
// start --> starting index
// end --> ending index
function findAllSequences($diff, $out, $start, $end)
{
    // We can't cover difference of more than n with 2n bits
    if (abs($diff) > (int)(($end - $start + 1) / 2))
        return;

    // if all bits are filled
    if ($start > $end)
    {
        // if sum of first n bits and last n bits are same
        if ($diff == 0)
            print(implode("",$out)." ");
        return;
    }

    // fill first bit as 0 and last bit as 1
    $out[$start] = '0';
    $out[$end] = '1';
    findAllSequences($diff + 1, $out, $start + 1, $end - 1);

    // fill first and last bits as 1
    $out[$start] = $out[$end] = '1';
    findAllSequences($diff, $out, $start + 1, $end - 1);

    // fill first and last bits as 0
    $out[$start] = $out[$end] = '0';
    findAllSequences($diff, $out, $start + 1, $end - 1);

    // fill first bit as 1 and last bit as 0
    $out[$start] = '1';
    $out[$end] = '0';
    findAllSequences($diff - 1, $out, $start + 1, $end - 1);
}

// Driver program

    // input number
    $n = 2;

    // allocate string containing 2*n characters
    $out=array_fill(0,2*$n,"");

    findAllSequences(0, $out, 0, 2*$n - 1);

// This code is contributed by chandan_jnu
?>

Javascript

<script>

    // JavaScript program to print even length binary
    // sequences whose sum of first and second
    // half bits is same

    // Function to print even length binary
    // sequences whose sum of first and
    // second half bits is same

    // diff --> difference between sums of
    // first n bits
    // and last n bits
    // out --> output array
    // start --> starting index
    // end --> ending index
    function findAllSequences(diff, outt, start, end)
    {

        // We can't cover difference of
        // more than n with 2n bits
        if (Math.abs(diff) > parseInt((end - start + 1) / 2, 10))
            return;

        // if all bits are filled
        if (start > end)
        {

            // if sum of first n bits and
            // last n bits are same
            if (diff == 0)
            {
                document.write(outt.join(""));
                document.write(" ");
            }
            return;
        }

        // fill first bit as 0 and last bit
        // as 1
        outt[start] = '0';
        outt[end] = '1';
        findAllSequences(diff + 1, outt, start + 1, end - 1);

        // fill first and last bits as 1
        outt[start] = outt[end] = '1';
        findAllSequences(diff, outt, start + 1, end - 1);

        // fill first and last bits as 0
        outt[start] = outt[end] = '0';
        findAllSequences(diff, outt, start + 1, end - 1);

        // fill first bit as 1 and last
        // bit as 0
        outt[start] = '1';
        outt[end] = '0';
        findAllSequences(diff - 1, outt, start + 1, end - 1);
    }

    // input number
    let n = 2;

    // allocate string containing 2*n
    // characters
    let outt = new Array(2 * n + 1);

    // null terminate output array
    outt[2 * n] = '\0';

    findAllSequences(0, outt, 0, 2*n - 1);

</script>

Output

0101 1111 1001 0110 0000 1010 

Time Complexity: O((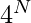)* N)

4^N because of 4 recursive calls, and N (simplified from 2N) for time spent printing strings of size 2N

Auxiliary Space: O(N) 

There is another approach by which we generate all possible strings of length n and store them in a list at an index representing their sum. Then, we iterate through each list and generate the strings of size 2n by printing each string with all other strings in the list adding up to the same value.

C++

// C++ program to implement the approach

#include <bits/stdc++.h>

using namespace std;

//function that generates the sequence
void generateSequencesWithSum(
    int n, vector<vector<string> >& sumToString,
    vector<string> sequence, int sumSoFar)
{
    // Base case, if there are no more binary digits to
    // include
    if (n == 0) {
        // add permutation to list of sequences with sum
        // corresponding to index
        string seq = "";
        for (int i = 0; i < sequence.size(); i++) {
            seq = seq + sequence[i];
        }
        vector<string> x = sumToString[sumSoFar];
        x.push_back(seq);
        sumToString[sumSoFar] = x;
        return;
    }
    // Generate sequence +0
    sequence.push_back("0");
    generateSequencesWithSum(n - 1, sumToString, sequence,
                             sumSoFar);
    sequence.erase(sequence.begin());
    // Generate sequence +1
    sequence.push_back("1");
    generateSequencesWithSum(n - 1, sumToString, sequence,
                             sumSoFar + 1);
    sequence.erase(sequence.begin());
}

// function to form permutations of the sequences
void permuteSequences(vector<vector<string> > sumToString)
{
    // There are 2^n substring in this list of lists
    for (int sumIndexArr = 0;
         sumIndexArr < sumToString.size(); sumIndexArr++) {
        // Append
        for (int sequence1 = 0;
             sequence1 < sumToString[sumIndexArr].size();
             sequence1++) {
            for (int sequence2 = 0;
                 sequence2
                 < sumToString[sumIndexArr].size();
                 sequence2++) {
                if (sumIndexArr == sumToString.size() - 1
                    && sequence1
                           == sumToString[sumIndexArr]
                                      .size()
                                  - 1
                    && sequence2
                           == sumToString[sumIndexArr]
                                      .size()
                                  - 1) {
                    cout << "1111 ";
                }
                else {
                    cout << sumToString[sumIndexArr]
                                       [sequence1]
                                + sumToString[sumIndexArr]
                                             [sequence2]
                         << " ";
                }
            }
        }
    }
}

// function that finds all the subsequences
void findAllSequences(int n)
{
    vector<vector<string> > sumToString;
    for (int i = 0; i < n + 1; i++) {
        sumToString.push_back(
            vector<string>()); // list of strings
                               // where index
                               // represents sum
    }
    generateSequencesWithSum(n, sumToString,
                             vector<string>(), 0);
    permuteSequences(sumToString);
}

// Driver Code
int main()
{

    // Function Call
    findAllSequences(2);
    return 0;
}

// this code is contributed by phasing17

Java

// Java program to implement the approach
import java.util.*;

class GFG {

    // function that finds all the subsequences
    static void findAllSequences(int n)
    {
        ArrayList<ArrayList<String> > sumToString
            = new ArrayList<ArrayList<String> >();
        for (int i = 0; i < n + 1; i++) {
            sumToString.add(
                new ArrayList<String>()); // list of strings
                                          // where index
                                          // represents sum
        }
        generateSequencesWithSum(
            n, sumToString, new ArrayList<String>(), 0);
        permuteSequences(sumToString);
    }
    static void generateSequencesWithSum(
        int n, ArrayList<ArrayList<String> > sumToString,
        ArrayList<String> sequence, int sumSoFar)
    {
        // Base case, if there are no more binary digits to
        // include
        if (n == 0) {
            // add permutation to list of sequences with sum
            // corresponding to index
            String seq = "";
            for (int i = 0; i < sequence.size(); i++) {
                seq = seq + sequence.get(i);
            }
            ArrayList<String> x = sumToString.get(sumSoFar);
            x.add(seq);
            sumToString.set(sumSoFar, x);
            return;
        }
        // Generate sequence +0
        sequence.add("0");
        generateSequencesWithSum(n - 1, sumToString,
                                 sequence, sumSoFar);
        sequence.remove(0);
        // Generate sequence +1
        sequence.add("1");
        generateSequencesWithSum(n - 1, sumToString,
                                 sequence, sumSoFar + 1);
        sequence.remove(0);
    }

    // function to form permutations of the sequences
    static void permuteSequences(
        ArrayList<ArrayList<String> > sumToString)
    {
        // There are 2^n substring in this list of lists
        for (int sumIndexArr = 0;
             sumIndexArr < sumToString.size();
             sumIndexArr++) {
            // Append
            for (int sequence1 = 0;
                 sequence1
                 < sumToString.get(sumIndexArr).size();
                 sequence1++) {
                for (int sequence2 = 0;
                     sequence2
                     < sumToString.get(sumIndexArr).size();
                     sequence2++) {
                    if (sumIndexArr
                            == sumToString.size() - 1
                        && sequence1
                               == sumToString
                                          .get(sumIndexArr)
                                          .size()
                                      - 1
                        && sequence2
                               == sumToString
                                          .get(sumIndexArr)
                                          .size()
                                      - 1) {
                        System.out.print("1111");
                    }
                    else {
                        System.out.println(
                            sumToString.get(sumIndexArr)
                                .get(sequence1)
                            + sumToString.get(sumIndexArr)
                                  .get(sequence2));
                    }
                }
            }
        }
    }
    // Driver Code
    public static void main(String[] args)
    {
        // Function Call
        findAllSequences(2);
    }

    // this code is contributed by phasing17
}

Python3

def findAllSequences(n):
    sumToString = [[] for x in range(n+1)] # list of strings where index represents sum
    generateSequencesWithSum(n, sumToString, [], 0)
    permuteSequences(sumToString)


def generateSequencesWithSum(n, sumToString, sequence, sumSoFar):
    #Base case, if there are no more binary digits to include
    if n == 0:
        sumToString[sumSoFar].append("".join(sequence)) #add permutation to list of sequences with sum corresponding to index
        return
    #Generate sequence +0
    sequence.append("0")
    generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar)
    sequence.pop()
    #Generate sequence +1
    sequence.append("1")
    generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar+1)
    sequence.pop()


def permuteSequences(sumToString):
    #There are 2^n substring in this list of lists
    for sumIndexArr in sumToString:
        # Append
        for sequence1 in sumIndexArr:
            for sequence2 in sumIndexArr:
                print(sequence1 + sequence2)


findAllSequences(2)

#Contribution by Xavier Jean Baptiste

C#

using System;
using System.Collections.Generic;
class GFG {

  static void findAllSequences(int n)
  {
    List<List<string>> sumToString = new List<List<string>>();
    for(int i = 0; i < n + 1; i++)
    {
      sumToString.Add(new List<string>()); // list of strings where index represents sum
    }
    generateSequencesWithSum(n, sumToString, new List<string>(), 0);
    permuteSequences(sumToString);
  }

  static void generateSequencesWithSum(int n, List<List<string>> sumToString, List<string> sequence, int sumSoFar)
  {
    // Base case, if there are no more binary digits to include
    if(n == 0)
    {
      //add permutation to list of sequences with sum corresponding to index
      string seq = "";
      for(int i = 0; i < sequence.Count; i++)
      {
        seq = seq + sequence[i];
      }
      sumToString[sumSoFar].Add(seq);
      return;
    }
    // Generate sequence +0
    sequence.Add("0");
    generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar);
    sequence.RemoveAt(0);
    // Generate sequence +1
    sequence.Add("1");
    generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar+1);
    sequence.RemoveAt(0);
  }

  static void permuteSequences(List<List<string>> sumToString)
  {
    // There are 2^n substring in this list of lists
    for(int sumIndexArr = 0; sumIndexArr < sumToString.Count; sumIndexArr++)
    {
      // Append
      for(int sequence1 = 0; sequence1 < sumToString[sumIndexArr].Count; sequence1++)
      {
        for(int sequence2 = 0; sequence2 < sumToString[sumIndexArr].Count; sequence2++)
        {
          if(sumIndexArr == sumToString.Count-1 && sequence1 == sumToString[sumIndexArr].Count-1 && sequence2 == sumToString[sumIndexArr].Count-1)
          {
            Console.Write("1111");
          }
          else
          {
            Console.WriteLine(sumToString[sumIndexArr][sequence1] + sumToString[sumIndexArr][sequence2]);
          }
        }
      }
    }
  }

  static void Main() {
    findAllSequences(2);
  }
}

// This code is contributed by divyesh072019.

Javascript

<script>
    function findAllSequences(n)
    {
      let sumToString = [];
      for(let i = 0; i < n + 1; i++)
      {
          sumToString.push([]); // list of strings where index represents sum
      }
      generateSequencesWithSum(n, sumToString, [], 0);
      permuteSequences(sumToString);
    }

    function generateSequencesWithSum(n, sumToString, sequence, sumSoFar)
    {
      // Base case, if there are no more binary digits to include
      if(n == 0)
      {
            //add permutation to list of sequences with sum corresponding to index
          sumToString[sumSoFar].push(sequence.join(""));
          return;
      }
      // Generate sequence +0
      sequence.push("0");
      generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar);
      sequence.shift();
      // Generate sequence +1
      sequence.push("1");
      generateSequencesWithSum(n-1, sumToString, sequence, sumSoFar+1);
      sequence.shift();
    }

    function permuteSequences(sumToString)
    {
      // There are 2^n substring in this list of lists
      for(let sumIndexArr = 0; sumIndexArr < sumToString.length; sumIndexArr++)
      {
          // Append
          for(let sequence1 = 0; sequence1 < sumToString[sumIndexArr].length; sequence1++)
          {
              for(let sequence2 = 0; sequence2 < sumToString[sumIndexArr].length; sequence2++)
              {
                    if(sumIndexArr == sumToString.length-1 && sequence1 == sumToString[sumIndexArr].length-1 && sequence2 == sumToString[sumIndexArr].length-1)
                  {
                      document.write("1111");
                  }
                  else
                  {
                      document.write(sumToString[sumIndexArr][sequence1] + sumToString[sumIndexArr][sequence2] + "</br>");
                  }
              }
          }
      }
    }

    findAllSequences(2);

    // This code is contributed by decode2207.
</script>

Output

0000 0101 0110 1001 1010 1111 

Time complexity analysis:

generateSequencesWithSum = O((2^N)*N)

• 2^N: we generate all permutation of binary strings of size N
• N: convert the list of characters to a string and store into array. This is done in the base case.

permuteSequences = O((2^N) * N!/(N/2)!² * N)

• 2^N: we iterate through all the string generated of size n
• N!/(N/2)!²: This one is a bit challenging to explain

let’s take N = 2 as an example. Our array of possible sequence of size n would be:

array index	0	1	2
list of strings	00	01,10	11

In the list of strings which the index represents the sum, we get the count of strings of size 2n by using “n choose k” formula. I our case it would be nCk *nCk where k represents the number of 1s in each half of the string of size 2n:

k = 0, we have (2C0)^2 = 1 string (0000)

k =  1, we have (2C1)^2 string = 4 strings(0101 0110 1001 1010)

k = 2, we have (2c2)^2 = 1 string (1111)

We get our longest list of string when k = N/2, hence _NC_N/2 = N!/[(N/2)! * (N – N/2)!]  which simplifies to _NC_N/2 = N!/(N/2)!²

Hence, for each element, we must iterate through, at most, _NC_N/2 for forming strings of length 2N

Without formal proof, if we graph 2^N and N!/(N/2)!², we see that 2^N has a faster growth rate than the latter. Therefore O(2^N* N!/(N/2)² ) < O(2^N*2^N) = O(2²ⁿ) = O(4^N)

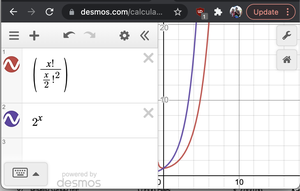
Graph of 2^x and nC(n/2)

• N: we must print each string of size 2N

Finally we can ignore the time complexity of generateSequencesWithSum because permuteSequence is the leading term

Time complexity: O(2^N * N!/(N/2)!² * N) (better than the first solution of O((4^N) * N, see explanation above for further details)

Auxiliary space: O(2^N) because we store all binary string permutations of size N

This article is contributed by Aditya Goel and improved by Xavier Jean Baptiste. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Java

import java.util.*;

class GFG {
    static class FirstHalf {
        String data;
        int sum;

        FirstHalf(String data, int sum) {
            this.data = data;
            this.sum = sum;
        }
    }

    //MAP: Key -> sum of bits; Value -> All possible permutation with respective sum
    static Map<Integer, ArrayList<String>> map = new HashMap<>();

    //first N-half bits
    static List<FirstHalf> firstHalf = new ArrayList<>();

    //function to find sum of the bits from a String
    public static int sumOfString(String s) {
        int sum = 0;
        //ex: converts "1" to 1 -> (ASCII('1') - ASCII('0') = 1)
        for(char c: s.toCharArray()) {
            sum += c - '0';
        }
        return sum;
    }

    public static void perm(String p, char[] bin, int level, int n) {
        //p: processed string(processed permutation at current level)
        //bin: {'0', '1'}
        //l: current level of recursion tree (leaf/solution level = 0)
        //n: total levels
        if(level == 0) {
            //at solution level find sum of the current permutation
            int sum = sumOfString(p);
            //store current permutation to firstHalf list
            firstHalf.add(new FirstHalf(p, sum));
            //put current permutation to its respective sum value
            map.putIfAbsent(sum, new ArrayList<String>());
            map.get(sum).add(p);
            return;
        }

        //generate calls for permutation
        //working: first solution with all 0s, then replacing last 0 with 1 and so on...
        for(char c: bin) {
            perm(p+c, bin, level-1, n);
        }
    }

    public static void result() {
        int i = 0;
        for(FirstHalf first: firstHalf) {
            //for each firstHalf string
            //find sum of the bits of current string
            int sum = first.sum;
            //retrieve respective secondHalf from map based on sum key
            ArrayList<String> secondHalf = map.get(sum);
            for(String second: secondHalf) {
                //append first and second half and print
                System.out.print(first.data+second+" ");
                //after every 6 solution line is changed in output
                //only for formatting below lines could be removed
                i++;
                if(i % 6 == 0)
                    System.out.println();
            }
        }
    }


    public static void main(String[] args) {
        char[] up = {'0', '1'};
        int n = 2;
        perm("", up, n, n);
        result();
    }
}
//Code contributed by Animesh Singh

Output

0000 0101 0110 1001 1010 1111 

Algorithm:

1. Generate all binary permutations of size n

2. Calculate sum of the bits of each permutation and remember it for second half

[for ex: for n=2, remember there are two strings with sum = 1 i.e. “01”, “10” ]

3. Iterate all the generated permutations and for each of them append the second half according to the sum of the bits

Time complexity analysis:

sumOfString() = O(N) : traverse each bit and add it to sum

perm() = O(2^N * N)

2N * N : we generate all permutations of binary bits of size N and find sum of the bits for each permutation

result() = O((2^N) * (N!/(N/2)!)2)

2^N: we iterate through all possible permutations of size N (first-Half)
NCN/2 = N!/(N/2)!² : (second-Half maximum size) : explanation below:

let’s take N = 4 as an example.:

//Hash-Map looks like

0 -> [0000] …………………………..(list-size: 4C0 = 1)
1 -> [0001, 0010, 0100, 1000] …………………………..(list-size: 4C1 = 4)
2 -> [0011, 0101, 0110, 1001, 1010, 1100] …………………………..(list-size: 4C2 = 6)
3 -> [0111, 1011, 1101, 1110] …………………………..(list-size: 4C3 = 4)
4 -> [1111] …………………………..(list-size: 4C4 = 1)

We observe here that each list has a size of N choose Key which will be maximum at N choose N/2

Since we are iterating all the 2^N permutations and appending second half from the map. The map has the maximum sized list at N/2 position.

Worst case occurs in N/2 position where we’ve to traverse NCN/2 = N!/(N/2)!² permutations.

Time complexity: O(2^N * N!/(N/2)!² )

Auxiliary space: O(2^N) because we store all binary string permutations of size N