Find a point such that sum of the Manhattan distances is minimized
Last Updated :
31 Aug, 2022
Given N points in K dimensional space where 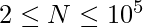 and
and 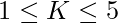 . The task is to determine the point such that the sum of Manhattan distances from this point to the N points is minimized.
. The task is to determine the point such that the sum of Manhattan distances from this point to the N points is minimized.
Manhattan distance is the distance between two points measured along axes at right angles. In a plane with p1 at (x1, y1) and p2 at (x2, y2), it is |x1 – x2| + |y1 – y2|.
Examples:
Input: N = 3, K = 3, Points = {1, 1, 1}, {2, 2, 2}, {3, 3, 3}
Output: 2 2 2
Input: N = 4, K = 4, Points = {1, 6, 9, 6}, {5, 2, 5, 7}, {2, 0, 1, 5}, {4, 6, 3, 9}
Output: 2 2 3 6
Approach: To minimize the Manhattan distance, all we have to do is just sort the points in all K dimensions and output the middle elements of each of the K dimensions.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void minDistance(int n, int k, vector<vector<int> >& point)
{
for (int i = 0; i < k; ++i)
sort(point[i].begin(), point[i].end());
for (int i = 0; i < k; ++i)
cout << point[i][(ceil((double)n / 2) - 1)] << " ";
}
int main()
{
int n = 4, k = 4;
vector<vector<int> > point = { { 1, 5, 2, 4 },
{ 6, 2, 0, 6 },
{ 9, 5, 1, 3 },
{ 6, 7, 5, 9 } };
minDistance(n, k, point);
return 0;
}
|
Java
import java.util.Arrays;
class GFG
{
static void minDistance(int n, int k,
int point[][])
{
for (int i = 0; i < k; i++)
Arrays.sort(point[i]);
for (int i = 0; i < k; i++)
System.out.print(point[i][(int)
Math.ceil((double)(n / 2) - 1)] + " ");
}
public static void main(String[] args)
{
int n = 4;
int k = 4;
int point[][] = { { 1, 5, 2, 4 },
{ 6, 2, 0, 6 },
{ 9, 5, 1, 3 },
{ 6, 7, 5, 9 } };
minDistance(n, k, point);
}
}
|
Python
def minDistance(n, k, point):
for i in range(k):
point[i].sort()
for i in range(k):
print(point[i][((n + 1) // 2) - 1], end =" ")
n = 4
k = 4
point = [[1, 5, 2, 4],
[6, 2, 0, 6],
[9, 5, 1, 3],
[6, 7, 5, 9]]
minDistance(n, k, point)
|
C#
using System;
class GFG
{
static void minDistance(int n, int k,
int[][] point)
{
for (int i = 0; i < k; i++)
Array.Sort(point[i]);
for (int i = 0; i < k; i++)
System.Console.Write(point[i][(int)
Math.Ceiling((double)(n / 2) - 1)] + " ");
}
public static void Main()
{
int n = 4;
int k = 4;
int[][] point = new int[][]{ new int[]{ 1, 5, 2, 4 },
new int[]{ 6, 2, 0, 6 },
new int[]{ 9, 5, 1, 3 },
new int[]{ 6, 7, 5, 9 } };
minDistance(n, k, point);
}
}
|
PHP
<?php
function minDistance($n, $k, &$point)
{
for ($i = 0; $i < $k; ++$i)
sort($point[$i]);
for ($i = 0; $i < $k; ++$i)
echo $point[$i][(ceil(
(double)$n / 2) - 1)] . " ";
}
$n = 4;
$k = 4;
$point = array(array( 1, 5, 2, 4 ),
array( 6, 2, 0, 6 ),
array( 9, 5, 1, 3 ),
array( 6, 7, 5, 9 ));
minDistance($n, $k, $point);
?>
|
Javascript
<script>
function minDistance(n,k,points)
{
for (let i = 0; i < k; i++)
(point[i]).sort(function(a,b){return a-b;});
for (let i = 0; i < k; i++)
document.write(point[i][
Math.ceil((n / 2) - 1)] + " ");
}
let n = 4;
let k = 4;
let point = [[1, 5, 2, 4],
[6, 2, 0, 6],
[9, 5, 1, 3],
[6, 7, 5, 9]];
minDistance(n, k, point);
</script>
|
Time Complexity: O(k*nlog(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...