Find a permutation of 2N numbers such that the result of given expression is exactly 2K
Last Updated :
23 Jun, 2022
Given two integers N and K, the task is to find a permutation of first 2*N natural numbers such that the following equation is satisfied.
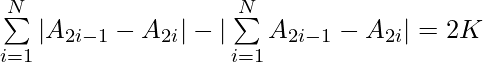
Note: The value of K will always be less than or equal to N.
Examples:
Input : N = 1, K = 0
Output : 1 2
The result of the above expression will be:
|1-2|-|1-2| =0
Input : N = 2, K = 1
Output : 2 1 3 4
The result of the above expression will be:
(|2-1|+|3-4|)-(|2-1+3-4|) = 2
Approach:
Consider the sorted permutation:
1, 2, 3, 4, 5, 6....
The result of the expression will come out to be exactly 0. If we swap any 2 indices 2i-1 and 2i, the result will increase by exactly 2. So we need to make K such swaps.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printPermutation(int n, int k)
{
for (int i = 1; i <= n; i++) {
int x = 2 * i - 1;
int y = 2 * i;
if (i <= k)
cout << y << " " << x << " ";
else
cout << x << " " << y << " ";
}
}
int main()
{
int n = 2, k = 1;
printPermutation(n, k);
return 0;
}
|
Java
class GFG
{
static void printPermutation(int n, int k)
{
for (int i = 1; i <= n; i++)
{
int x = 2 * i - 1;
int y = 2 * i;
if (i <= k)
System.out.print(y + " " + x + " ");
else
System.out.print(x + " " + y + " ");
}
}
public static void main(String []args)
{
int n = 2, k = 1;
printPermutation(n, k);
}
}
|
Python3
def printPermutation(n, k) :
for i in range(1, n + 1) :
x = 2 * i - 1;
y = 2 * i;
if (i <= k) :
print(y, x, end = " ");
else :
print(x, y, end = " ");
if __name__ == "__main__" :
n = 2; k = 1;
printPermutation(n, k);
|
C#
using System;
class GFG
{
static void printPermutation(int n, int k)
{
for (int i = 1; i <= n; i++)
{
int x = 2 * i - 1;
int y = 2 * i;
if (i <= k)
Console.Write(y + " " + x + " ");
else
Console.Write(x + " " + y + " ");
}
}
public static void Main()
{
int n = 2, k = 1;
printPermutation(n, k);
}
}
|
PHP
<?php
function printPermutation($n, $k)
{
for ($i = 1; $i <= $n; $i++)
{
$x = 2 * $i - 1;
$y = 2 * $i;
if ($i <= $k)
echo $y . " " . $x . " ";
else
echo $x . " " . $y . " ";
}
}
$n = 2;
$k = 1;
printPermutation($n, $k);
?>
|
Javascript
<script>
function printPermutation( n, k)
{
for (var i = 1; i <= n; i++)
{
var x = 2 * i - 1;
var y = 2 * i;
if (i <= k)
document.write(y + " " + x + " ");
else
document.write(x + " " + y + " ");
}
}
var n = 2, k = 1;
printPermutation(n, k);
</script>
|
Time Complexity: O(N), since there runs a loop from 1 to n.
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...