Find a pair of elements swapping which makes sum of two arrays same
Last Updated :
29 Mar, 2024
Given two arrays of integers, find a pair of values (one value from each array) that you can swap to give the two arrays the same sum.
Examples:
Input: A[] = {4, 1, 2, 1, 1, 2}, B[] = (3, 6, 3, 3)
Output: {1, 3}
Sum of elements in A[] = 11
Sum of elements in B[] = 15
To get same sum from both arrays, we
can swap following values:
1 from A[] and 3 from B[]
Input: A[] = {5, 7, 4, 6}, B[] = {1, 2, 3, 8}
Output: 6 2
Method 1 (Naive Implementation):
Iterate through the arrays and check all pairs of values. Compare new sums or look for a pair with that difference.
C++
#include <iostream>
using namespace std;
int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
void findSwapValues(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
int newsum1, newsum2, val1, val2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
newsum1 = sum1 - A[i] + B[j];
newsum2 = sum2 - B[j] + A[i];
if (newsum1 == newsum2) {
val1 = A[i];
val2 = B[j];
}
}
}
cout << val1 << " " << val2;
}
int main()
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = sizeof(A) / sizeof(A[0]);
int B[] = { 3, 6, 3, 3 };
int m = sizeof(B) / sizeof(B[0]);
findSwapValues(A, n, B, m);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static void findSwapValues(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
int newsum1, newsum2, val1 = 0, val2 = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
newsum1 = sum1 - A[i] + B[j];
newsum2 = sum2 - B[j] + A[i];
if (newsum1 == newsum2)
{
val1 = A[i];
val2 = B[j];
}
}
}
System.out.println(val1+" "+val2);
}
public static void main (String[] args)
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = A.length;
int B[] = { 3, 6, 3, 3 };
int m = B.length;
findSwapValues(A, n, B, m);
}
}
|
Python3
def getSum(X):
sum=0
for i in X:
sum+=i
return sum
def findSwapValues(A,B):
sum1=getSum(A)
sum2=getSum(B)
k=False
val1,val2=0,0
for i in A:
for j in B:
newsum1=sum1-i+j
newsum2=sum2-j+i
if newsum1 ==newsum2:
val1=i
val2=j
k=True
break
if k==True:
break
print (val1,val2)
return
A=[4,1,2,1,1,2]
B=[3,6,3,3]
findSwapValues(A,B)
|
C#
using System;
class GFG
{
static int getSum(int[] X, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static void findSwapValues(int[] A, int n,
int[] B, int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
int newsum1, newsum2,
val1 = 0, val2 = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
newsum1 = sum1 - A[i] + B[j];
newsum2 = sum2 - B[j] + A[i];
if (newsum1 == newsum2)
{
val1 = A[i];
val2 = B[j];
}
}
}
Console.Write(val1 + " " + val2);
}
public static void Main ()
{
int[] A = { 4, 1, 2, 1, 1, 2 };
int n = A.Length;
int[] B = { 3, 6, 3, 3 };
int m = B.Length;
findSwapValues(A, n, B, m);
}
}
|
PHP
<?php
function getSum($X, $n)
{
$sum = 0;
for ($i = 0; $i < $n; $i++)
$sum += $X[$i];
return $sum;
}
function findSwapValues($A, $n, $B, $m)
{
$sum1 = getSum($A, $n);
$sum2 = getSum($B, $m);
for ($i = 0; $i < $n; $i++)
{
for ($j = 0; $j < $m; $j++)
{
$newsum1 = $sum1 - $A[$i] + $B[$j];
$newsum2 = $sum2 - $B[$j] + $A[$i];
if ($newsum1 == $newsum2)
{
$val1 = $A[$i];
$val2 = $B[$j];
}
}
}
echo $val1 . " " . $val2;
}
$A = array(4, 1, 2, 1, 1, 2 );
$n = sizeof($A);
$B = array(3, 6, 3, 3 );
$m = sizeof($B);
findSwapValues($A, $n, $B, $m);
?>
|
Javascript
<script>
function getSum(X,n)
{
let sum = 0;
for (let i = 0; i < n; i++)
sum += X[i];
return sum;
}
function findSwapValues(A,n,B,m)
{
let sum1 = getSum(A, n);
let sum2 = getSum(B, m);
let newsum1, newsum2, val1 = 0, val2 = 0;
for (let i = 0; i < n; i++)
{
for (let j = 0; j < m; j++)
{
newsum1 = sum1 - A[i] + B[j];
newsum2 = sum2 - B[j] + A[i];
if (newsum1 == newsum2)
{
val1 = A[i];
val2 = B[j];
}
}
}
document.write(val1+" "+val2);
}
let A=[4, 1, 2, 1, 1, 2];
let n = A.length;
let B=[3, 6, 3, 3 ];
let m = B.length;
findSwapValues(A, n, B, m);
</script>
|
Time Complexity :- O(n*m)
Space Complexity : O(1)
Method 2 -> Other Naive implementation
We are looking for two values, a and b, such that:
sumA - a + b = sumB - b + a
2a - 2b = sumA - sumB
a - b = (sumA - sumB) / 2
Therefore, we’re looking for two values that have a specific target difference: (sumA – sumB) / 2.
C++
#include <iostream>
using namespace std;
int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
int getTarget(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
void findSwapValues(int A[], int n, int B[], int m)
{
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int val1, val2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (A[i] - B[j] == target) {
val1 = A[i];
val2 = B[j];
}
}
}
cout << val1 << " " << val2;
}
int main()
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = sizeof(A) / sizeof(A[0]);
int B[] = { 3, 6, 3, 3 };
int m = sizeof(B) / sizeof(B[0]);
findSwapValues(A, n, B, m);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static int getTarget(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
static void findSwapValues(int A[], int n, int B[], int m)
{
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int val1 = 0, val2 = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (A[i] - B[j] == target)
{
val1 = A[i];
val2 = B[j];
}
}
}
System.out.println(val1+" "+val2);
}
public static void main (String[] args)
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = A.length;
int B[] = { 3, 6, 3, 3 };
int m = B.length;
findSwapValues(A, n, B, m);
}
}
|
Python3
def getSum(X):
sum=0
for i in X:
sum+=i
return sum
def getTarget(A,B):
sum1=getSum(A)
sum2=getSum(B)
if( (sum1-sum2)%2!=0):
return 0
return (sum1-sum2)//2
def findSwapValues(A,B):
target=getTarget(A,B)
if target==0:
return
flag=False
val1,val2=0,0
for i in A:
for j in B:
if i-j == target:
val1=i
val2=j
flag=True
break
if flag==True:
break
print (val1,val2)
return
A=[4,1,2,1,1,2]
B=[3,6,3,3]
findSwapValues(A,B)
|
C#
using System;
class GFG
{
static int getSum(int []X, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static int getTarget(int []A, int n, int []B, int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
static void findSwapValues(int []A, int n, int []B, int m)
{
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int val1 = 0, val2 = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (A[i] - B[j] == target)
{
val1 = A[i];
val2 = B[j];
}
}
}
Console.Write(val1+" "+val2);
}
public static void Main ()
{
int []A = { 4, 1, 2, 1, 1, 2 };
int n = A.Length;
int []B = { 3, 6, 3, 3 };
int m = B.Length;
findSwapValues(A, n, B, m);
}
}
|
PHP
<?php
function getSum($X, $n)
{
$sum = 0;
for ($i = 0; $i < $n; $i++)
$sum += $X[$i];
return $sum;
}
function getTarget($A, $n, $B, $m)
{
$sum1 = getSum($A, $n);
$sum2 = getSum($B, $m);
if (($sum1 - $sum2) % 2 != 0)
return 0;
return (($sum1 - $sum2) / 2);
}
function findSwapValues($A, $n, $B, $m)
{
$target = getTarget($A, $n, $B, $m);
if ($target == 0)
return;
for ($i = 0; $i < $n; $i++)
{
for ($j = 0; $j < $m; $j++)
{
if ($A[$i] - $B[$j] == $target)
{
$val1 = $A[$i];
$val2 = $B[$j];
}
}
}
echo $val1 . " " . $val2;
}
$A = array(4, 1, 2, 1, 1, 2);
$n = sizeof($A);
$B = array(3, 6, 3, 3);
$m = sizeof($B);
findSwapValues($A, $n, $B, $m);
?>
|
Javascript
<script>
function getSum(X,n)
{
let sum = 0;
for (let i = 0; i < n; i++)
sum += X[i];
return sum;
}
function getTarget(A,n,B,m)
{
let sum1 = getSum(A, n);
let sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
function findSwapValues(A,n,B,m)
{
let target = getTarget(A, n, B, m);
if (target == 0)
return;
let val1 = 0, val2 = 0;
for (let i = 0; i < n; i++)
{
for (let j = 0; j < m; j++)
{
if (A[i] - B[j] == target)
{
val1 = A[i];
val2 = B[j];
}
}
}
document.write(val1+" "+val2+"<br>");
}
let A=[4, 1, 2, 1, 1, 2];
let n = A.length;
let B=[3, 6, 3, 3 ];
let m = B.length;
findSwapValues(A, n, B, m);
</script>
|
Time Complexity :- O(n*m)
Space Complexity :- O(1)
Method 3 -> Optimized Solution :-
- Sort the arrays.
- Traverse both array simultaneously and do following for every pair.
- If the difference is too small then, make it bigger by moving ‘a’ to a bigger value.
- If it is too big then, make it smaller by moving b to a bigger value.
- If it’s just right, return this pair.
Below image is a dry run of the above approach:
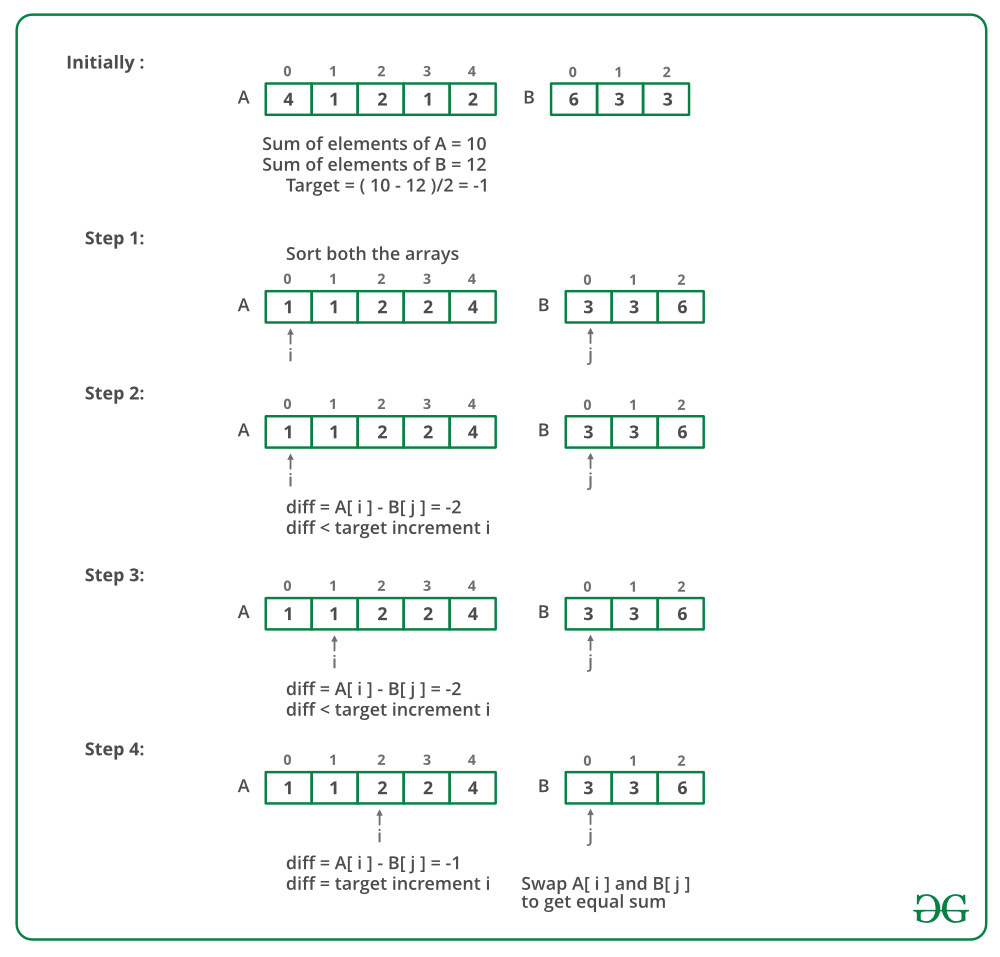
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
int getTarget(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
void findSwapValues(int A[], int n, int B[], int m)
{
sort(A, A + n);
sort(B, B + m);
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int i = 0, j = 0;
while (i < n && j < m) {
int diff = A[i] - B[j];
if (diff == target) {
cout << A[i] << " " << B[j];
return;
}
else if (diff < target)
i++;
else
j++;
}
}
int main()
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = sizeof(A) / sizeof(A[0]);
int B[] = { 1, 6, 3, 3 };
int m = sizeof(B) / sizeof(B[0]);
findSwapValues(A, n, B, m);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static int getSum(int X[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static int getTarget(int A[], int n, int B[], int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
static void findSwapValues(int A[], int n, int B[], int m)
{
Arrays.sort(A);
Arrays.sort(B);
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int i = 0, j = 0;
while (i < n && j < m)
{
int diff = A[i] - B[j];
if (diff == target)
{
System.out.println(A[i]+" "+B[i]);
return;
}
else if (diff < target)
i++;
else
j++;
}
}
public static void main (String[] args)
{
int A[] = { 4, 1, 2, 1, 1, 2 };
int n = A.length;
int B[] = { 3, 6, 3, 3 };
int m = B.length;
findSwapValues(A, n, B, m);
}
}
|
Python3
def getSum(X):
sum=0
for i in X:
sum+=i
return sum
def getTarget(A,B):
sum1=getSum(A)
sum2=getSum(B)
if( (sum1-sum2)%2!=0):
return 0
return (sum1-sum2)//2
def findSwapValues(A,B):
A.sort()
B.sort()
target=getTarget(A,B)
if(target==0):
return
i,j=0,0
while(i<len(A) and j<len(B)):
diff=A[i]-B[j]
if diff == target:
print (A[i],B[j])
return
elif diff <target:
i+=1
else:
j+=1
A=[4,1,2,1,1,2]
B=[3,6,3,3]
findSwapValues(A,B)
|
C#
using System;
class GFG
{
static int getSum(int []X, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += X[i];
return sum;
}
static int getTarget(int []A, int n, int []B, int m)
{
int sum1 = getSum(A, n);
int sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
static void findSwapValues(int []A, int n, int []B, int m)
{
Array.Sort(A);
Array.Sort(B);
int target = getTarget(A, n, B, m);
if (target == 0)
return;
int i = 0, j = 0;
while (i < n && j < m)
{
int diff = A[i] - B[j];
if (diff == target)
{
Console.WriteLine(A[i]+" "+B[i]);
return;
}
else if (diff < target)
i++;
else
j++;
}
}
public static void Main (String[] args)
{
int []A = { 4, 1, 2, 1, 1, 2 };
int n = A.Length;
int []B = { 3, 6, 3, 3 };
int m = B.Length;
findSwapValues(A, n, B, m);
}
}
|
Javascript
<script>
function getSum(X,n)
{
let sum = 0;
for (let i = 0; i < n; i++)
sum += X[i];
return sum;
}
function getTarget(A,n,B,m)
{
let sum1 = getSum(A, n);
let sum2 = getSum(B, m);
if ((sum1 - sum2) % 2 != 0)
return 0;
return ((sum1 - sum2) / 2);
}
function findSwapValues(A,n,B,m)
{
A.sort(function(a,b){return a-b;});
B.sort(function(a,b){return a-b;});
let target = getTarget(A, n, B, m);
if (target == 0)
return;
let i = 0, j = 0;
while (i < n && j < m)
{
let diff = A[i] - B[j];
if (diff == target)
{
document.write(A[i]+" "+B[j]);
return;
}
else if (diff < target)
i++;
else
j++;
}
}
let A=[4, 1, 2, 1, 1, 2 ];
let n = A.length;
let B=[3, 6, 3, 3 ];
let m = B.length;
findSwapValues(A, n, B, m);
</script>
|
Time Complexity :-
If arrays are sorted : O(n + m)
If arrays aren’t sorted : O(nlog(n) + mlog(m))
Space Complexity : O(1)
Method 4 (Hashing)
We can solve this problem in O(m+n) time and O(m) auxiliary space. Below are algorithmic steps.
// assume array1 is small i.e. (m < n)
// where m is array1.length and n is array2.length
1. Find sum1(sum of small array elements) and sum2
(sum of larger array elements). // time O(m+n)
2. Make a hashset for small array(here array1).
3. Calculate diff as (sum1-sum2)/2.
4. Run a loop for array2
for (int i equal to 0 to n-1)
if (hashset contains (array2[i]+diff))
print array2[i]+diff and array2[i]
set flag and break;
5. If flag is unset then there is no such kind of
pair.
Thanks to nicky khan for suggesting method 4.
If you like GeeksforGeeks (We know you do!) and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org.
Another Approach:
We can also solve this problem in linear time using hashing. Let us assume that sum of the elements of the first array a[] is s1, and of the second array b[] is s2. Also suppose that a pair to be swapped is (p, q), where p belongs to a[] and q belongs to b[]. Therefore, we have the equation s1 – p + q = s2 – q + p, i.e. 2q = s2 – s1 + 2p. Since both 2p and 2q are even integers, the difference s2 – s1 must be an even integer too. So, given any p, our aim is to find an appropriate q satisfying the above conditions.
Below is an implementation of the said approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findSwapValues(int a[], int m, int b[], int n);
int main()
{
int a[] = { 4, 1, 2, 1, 1, 2 }, b[] = { 1, 6, 3, 3 };
int m, n;
m = sizeof(a) / sizeof(int),
n = sizeof(b) / sizeof(int);
findSwapValues(a, m, b, n);
return 0;
}
void findSwapValues(int a[], int m, int b[], int n)
{
unordered_set<int> x,
y;
unordered_set<int>::iterator p, q;
int s1, s2;
int i;
s1 = 0;
for (i = 0; i < m;
i++)
s1 += a[i], x.insert(a[i]);
s2 = 0;
for (i = 0; i < n; i++)
s2 += b[i], y.insert(b[i]);
if ((s1 - s2) % 2)
{
printf("No such values exist.\n");
return;
}
for (p = x.begin(); p != x.end(); p++) {
q = y.find(
((s2 - s1) + 2 * *p)
/ 2);
if (q != y.end()) {
printf("%d %d\n", *p, *q);
return;
}
}
printf("No such values exist.\n");
}
|
Java
import java.util.*;
public class Solution {
static void findSwapValues(int a[], int m, int b[],
int n)
{
HashSet<Integer> x = new HashSet<>();
HashSet<Integer> y = new HashSet<>();
int s1, s2;
int i;
s1 = 0;
for (i = 0; i < m; i++) {
s1 += a[i];
x.add(a[i]);
}
s2 = 0;
for (i = 0; i < n; i++) {
s2 += b[i];
y.add(b[i]);
}
if ((s1 - s2) % 2 != 0)
{
System.out.println("No such values exist.");
return;
}
for (Integer p : x) {
int q = ((s2 - s1) + 2 * p) / 2;
if (y.contains(q)) {
System.out.println(p + " " + q);
return;
}
}
System.out.println("No such values exist.");
}
public static void main(String[] args)
{
int a[] = { 4, 1, 2, 1, 1, 2 };
int b[] = { 1, 6, 3, 3 };
int m = a.length;
int n = b.length;
findSwapValues(a, m, b, n);
}
}
|
Python3
def findSwapValues(a, m, b, n):
x, y = {}, {}
s1, s2 = 0, 0
for i in range(m):
s1 += a[i]
x[a[i]] = x.get(a[i], 0) + 1
for i in range(n):
s2 += b[i]
y[b[i]] = y.get(b[i], 0) + 1
if (s1 - s2) % 2:
print("No such values exist.")
return
for p in x:
q = ((s2 - s1)//2) + p
if q in y:
print(p, q)
return
print("No such values exist.")
if __name__ == "__main__":
a = [4, 1, 2, 1, 1, 2]
b = [1, 6, 3, 3]
m = len(a)
n = len(b)
findSwapValues(a, m, b, n)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static void findSwapValues(int[] a, int m, int[] b,
int n)
{
HashSet<int> x = new HashSet<int>();
HashSet<int> y = new HashSet<int>();
int s1, s2;
int i;
s1 = 0;
for (i = 0; i < m; i++) {
s1 += a[i];
x.Add(a[i]);
}
s2 = 0;
for (i = 0; i < n; i++) {
s2 += b[i];
y.Add(b[i]);
}
if ((s1 - s2) % 2
!= 0)
{
Console.Write("No such values exist");
return;
}
foreach(int p in x)
{
int q = ((s2 - s1) + 2 * p)
/ 2;
if (y.Contains(q)) {
Console.Write(p + " " + q);
return;
}
}
Console.Write("No such values exist");
}
public static void Main(string[] args)
{
int[] a = { 4, 1, 2, 1, 1, 2 };
int[] b = { 1, 6, 3, 3 };
int m = 6;
int n = 4;
findSwapValues(a, m, b, n);
}
}
|
Javascript
function findSwapValues(a, m, b, n)
{
let x = new Set();
let y = new Set();
let s1, s2;
let i;
s1 = 0;
for (i = 0; i < m; i++){
s1 += a[i];
x.add(a[i]);
}
s2 = 0;
for (i = 0; i < n; i++){
s2 += b[i];
y.add(b[i]);
}
if ((s1 - s2) % 2)
{
console.log("No such values exist.");
return;
}
for(let p of x){
let ele = ((s2-s1) + 2**p)/ 2;
let q = y.has(ele);
if(q){
console.log(p + " " + ele);
return;
}
}
console.log("No such values exist.");
}
let a = [ 4, 1, 2, 1, 1, 2 ];
let b = [ 1, 6, 3, 3 ];
let m, n;
m = a.length;
n = b.length;
findSwapValues(a, m, b, n);
|
Time complexity of the above code is O(m + n), where m and n respectively represent the sizes of the two input arrays, and space complexity O(s + t), where s and t respectively represent the number of distinct elements present in the two input arrays.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...