Fibonomial coefficient and Fibonomial triangle
Last Updated :
23 Nov, 2022
Fibonomial Coefficient:
In mathematics, the Fibonomial coefficients or Fibonacci-binomial coefficients are defined as
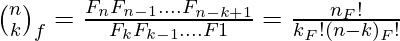
where n and k are non-negative integers, 0 ? k ? n, Fj is the j-th Fibonacci number and n!F is the nth Fibonorial, where 0!F, being the empty product, evaluates to 1.
The Fibonomial coefficients are all integers. Some special values are:
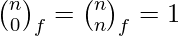
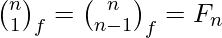
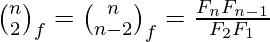
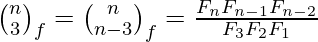
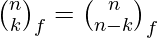
Fibonomial Triangle
The Fibonomial coefficients are similar to binomial coefficients and can be displayed in a triangle similar to Pascal’s triangle. The first eight rows are shown below.

The Recurrence Relation for Fibonomial Triangle:
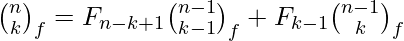
Given a positive integer n. The task is to print Fibonomial triangle of height n (or n + 1 rows).
Examples:
Input : n = 6
Output :
1
1 1
1 1 1
1 2 2 1
1 3 6 3 1
1 5 15 15 5 1
1 8 40 60 40 8 1
Input : n = 5
Output :
1
1 1
1 1 1
1 2 2 1
1 3 6 3 1
1 5 15 15 5 1
Below is the implementation of printing Fibonomial Triangle of height n:
C++
#include<bits/stdc++.h>
#define N 6
using namespace std;
void fib(int f[], int n)
{
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i-1] + f[i-2];
}
void fibcoef(int fc[][N+1], int f[], int n)
{
for (int i = 0; i <= n; i++)
fc[i][0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
int k = j;
while(k--)
fc[i][j] *= f[k];
k = 1;
while((j+1)!=k)
fc[i][j] /= f[k++];
}
}
}
void printFibonomialTriangle(int n)
{
int f[N+1] = { 0 };
fib(f, n);
int dp[N+1][N+1] = { 0 };
for (int i = 0; i <= n; i++)
dp[i][0] = dp[i][i] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < i; j++)
dp[i][j] = f[i-j+1]*dp[i-1][j-1] +
f[j-1]*dp[i-1][j];
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= i; j++)
cout << dp[i][j] << " ";
cout << endl;
}
}
int main()
{
int n = 6;
printFibonomialTriangle(n);
return 0;
}
|
Java
class GFG
{
static final int N=6;
static void fib(int f[], int n)
{
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i-1] + f[i-2];
}
static void fibcoef(int fc[][], int f[], int n)
{
for (int i = 0; i <= n; i++)
fc[i][0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
int k = j;
while(k > 0)
{
k--;
fc[i][j] *= f[k];
}
k = 1;
while((j + 1) != k)
fc[i][j] /= f[k++];
}
}
}
static void printFibonomialTriangle(int n)
{
int f[] = new int[N+1];
fib(f, n);
int dp[][] = new int[N + 1][N + 1];
for (int i = 0; i <= n; i++)
dp[i][0] = dp[i][i] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < i; j++)
dp[i][j] = f[i - j + 1] * dp[i - 1][j - 1] +
f[j-1]*dp[i-1][j];
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= i; j++)
System.out.print(dp[i][j] + " ");
System.out.println();
}
}
public static void main (String[] args)
{
int n = 6;
printFibonomialTriangle(n);
}
}
|
Python3
N = 6;
def fib(f, n):
f[0] = 0;
f[1] = 1;
for i in range(2, n + 1):
f[i] = f[i - 1] + f[i - 2];
def fibcoef(fc, f, n):
for i in range(n + 1):
fc[i][0] = 1;
for i in range(1, n + 1):
for j in range(1, i + 1):
k = j;
while(k > 0):
k -= 1;
fc[i][j] *= f[k];
k = 1;
while((j + 1) != k):
fc[i][j] /= f[k];
k += 1;
def printFibonomialTriangle(n):
f = [0] * (N + 1);
fib(f, n);
dp = [[0 for x in range(N + 1)]
for y in range(N + 1)];
for i in range(n + 1):
dp[i][0] = 1;
dp[i][i] = 1;
for i in range(1, n + 1):
for j in range(1, i):
dp[i][j] = (f[i - j + 1] * dp[i - 1][j - 1] +
f[j - 1] * dp[i - 1][j]);
for i in range(n + 1):
for j in range(i + 1):
print(dp[i][j], end = " ");
print("");
n = 6;
printFibonomialTriangle(n);
|
C#
using System;
class GFG
{
static int N = 6;
static void fib(int []f, int n)
{
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
}
static void fibcoef(int [,]fc, int []f, int n)
{
for (int i = 0; i <= n; i++)
fc[i,0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
int k = j;
while(k > 0)
{
k--;
fc[i, j] *= f[k];
}
k = 1;
while((j + 1) != k)
fc[i, j] /= f[k++];
}
}
}
static void printFibonomialTriangle(int n)
{
int []f = new int[N + 1];
fib(f, n);
int [,]dp = new int[N + 1, N + 1];
for (int i = 0; i <= n; i++)
dp[i, 0] = dp[i, i] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < i; j++)
dp[i,j] = f[i - j + 1] * dp[i - 1,j - 1] +
f[j - 1] * dp[i - 1, j];
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= i; j++)
Console.Write(dp[i,j] + " ");
Console.WriteLine();
}
}
public static void Main ()
{
int n = 6;
printFibonomialTriangle(n);
}
}
|
PHP
<?php
$N=6;
function fib(&$f, $n)
{
$f[0] = 0;
$f[1] = 1;
for ($i = 2; $i <= $n; $i++)
$f[$i] = $f[$i-1] + $f[$i-2];
}
function fibcoef($fc, $f, $n)
{
for ($i = 0; $i <= $n; $i++)
$fc[$i][0] = 1;
for ($i = 1; $i <= $n; $i++)
{
for ($j = 1; $j <= $i; $j++)
{
$k = $j;
while($k--)
$fc[$i][$j] *= $f[$k];
$k = 1;
while(($j+1)!=$k)
$fc[$i][$j] /= $f[$k++];
}
}
}
function printFibonomialTriangle($n)
{
global $N;
$f=array_fill(0,$N+1,0);
fib($f, $n);
$dp=array_fill(0,$N+1,array_fill(0,$N+1,0));
for ($i = 0; $i <= $n; $i++)
$dp[$i][0] = $dp[$i][$i] = 1;
for ($i = 1; $i <= $n; $i++)
{
for ($j = 1; $j < $i; $j++)
$dp[$i][$j] = $f[$i-$j+1]*$dp[$i-1][$j-1] +
$f[$j-1]*$dp[$i-1][$j];
}
for ($i = 0; $i <= $n; $i++)
{
for ($j = 0; $j <= $i; $j++)
echo $dp[$i][$j]." ";
echo "\n";
}
}
$n = 6;
printFibonomialTriangle($n);
?>
|
Javascript
<script>
var N = 6;
function fib(f , n) {
var i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
}
function fibcoef(fc , f , n) {
for (i = 0; i <= n; i++)
fc[i][0] = 1;
for (i = 1; i <= n; i++) {
for (j = 1; j <= i; j++) {
var k = j;
while (k > 0) {
k--;
fc[i][j] *= f[k];
}
k = 1;
while ((j + 1) != k)
fc[i][j] /= f[k++];
}
}
}
function printFibonomialTriangle(n) {
var f = Array(N + 1).fill(0);
fib(f, n);
var dp = Array(N + 1);
for(var i =0;i<N+1;i++)
dp[i] = Array(N + 1).fill(0);
for (i = 0; i <= n; i++)
dp[i][0] = dp[i][i] = 1;
for (i = 1; i <= n; i++) {
for (j = 1; j < i; j++)
dp[i][j] = f[i - j + 1] * dp[i - 1][j - 1] +
f[j - 1] * dp[i - 1][j];
}
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++)
document.write(dp[i][j] + " ");
document.write("<br/>");
}
}
var n = 6;
printFibonomialTriangle(n);
</script>
|
Output1
1 1
1 1 1
1 2 2 1
1 3 6 3 1
1 5 15 15 5 1
1 8 40 60 40 8 1
Time Complexity: O(n2)
Auxiliary Space: O(n2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...