Fibonacci modulo p

The Fibonacci sequence is defined as 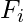= 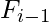+ 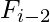where 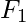= 1 and 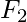= 1 are the seeds. 
For a given prime number p, consider a new sequence which is (Fibonacci sequence) mod p. For example for p = 5, the new sequence would be 1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4 … 
The minimal zero of the new sequence is defined as the first Fibonacci number that is a multiple of p or 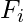mod p = 0. 
Given prime no p, find the minimal zero of the sequence Fibonacci modulo p.
Examples:

Input : 5
Output : 5
The fifth Fibonacci no (1 1 2 3 5) 
is divisible by 5 so 5 % 5 = 0.

Input : 7
Output : 8
The 8th Fibonacci no (1 1 2 3 5 8 13 21) 
is divisible by 7 so 21 % 7 = 0.

A simple approach is to keep calculating Fibonacci numbers and for each of them calculate Fi mod p. However if we observe this new sequence, let 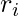denote the 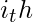term of the sequence, then it follows : 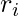= (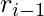+ 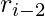) mod p. i.e. the remainder 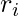is actually the sum of remainders of previous two terms of this series. Therefore instead of generating the Fibonacci sequence and then taking modulo of each term we simply add previous two remainders and then take its modulo p. 
Below is the implementation to find the minimal 0. 

C++

// C++ program to find minimal 0 Fibonacci
// for a prime number p
#include<bits/stdc++.h>
using namespace std;

// Returns position of first Fibonacci number
// whose modulo p is 0.
int findMinZero(int p)
{
    int first = 1, second = 1, number = 2, next = 1;
    while (next)
    {
        next = (first + second) % p;
        first = second;
        second = next;
        number++;
    }
    return number;
}

// Driver code
int main()
{
    int p = 7;
    cout << "Minimal zero is: "
        << findMinZero(p) << endl;
    return 0;
}

Java

// Java program to find minimal 0 Fibonacci
// for a prime number p
import java.io.*;

class FibZero
{
    // Function that returns position of first Fibonacci number
    // whose modulo p is 0
    static int findMinZero(int p)
    {
        int first = 1, second = 1, number = 2, next = 1;
        while (next > 0)
        {
            // add previous two remainders and
            // then take its modulo p.
            next = (first + second) % p;
            first = second;
            second = next;
            number++;
        }
        return number;
    }

    // Driver program
    public static void main (String[] args)
    {
        int p = 7;
        System.out.println("Minimal zero is " + findMinZero(p));
    }
}

Python3

# Python 3 program to find minimal
# 0 Fibonacci for a prime number p

# Returns position of first Fibonacci
# number whose modulo p is 0.
def findMinZero(p):
    first = 1
    second = 1
    number = 2
    next = 1

    while (next):
        next = (first + second) % p
        first = second
        second = next
        number = number + 1

    return number

# Driver code
if __name__ == '__main__':
    p = 7
    print("Minimal zero is:", findMinZero(p))

# This code is contributed by
# Surendra_Gangwar

C#

// C# program to find minimal 0
// Fibonacci for a prime number p
using System;

class GFG {

    // Function that returns position
    // of first Fibonacci number
    // whose modulo p is 0
    static int findMinZero(int p)
    {
        int first = 1, second = 1;
        int number = 2, next = 1;
        while (next > 0)
        {

            // add previous two
            // remainders and then
            // take its modulo p.
            next = (first + second) % p;
            first = second;
            second = next;
            number++;
        }
        return number;
    }

    // Driver program
    public static void Main ()
    {
        int p = 7;
        Console.WriteLine("Minimal zero "
              + "is :" + findMinZero(p));
    }
}

// This code is contributed by anuj_67.

PHP

<?php
// PHP program to find
// minimal 0 Fibonacci
// for a prime number p

// Returns position of
// first Fibonacci number
// whose modulo p is 0.
function findMinZero($p)
{
    $first = 1;
    $second = 1;
    $number = 2;
    $next = 1;
    while ($next)
    {
        $next = ($first +
                 $second) % $p;
        $first = $second;
        $second = $next;
        $number++;
    }

    return $number;
}

// Driver code
$p = 7;
echo "Minimal zero is: ",
    findMinZero($p), "\n";

// This code is contributed
// by akt_mit
?>

Javascript

<script>
// Javascript program to find
// minimal 0 Fibonacci
// for a prime number p

// Returns position of
// first Fibonacci number
// whose modulo p is 0.
function findMinZero(p)
{
    let first = 1;
    let second = 1;
    let number = 2;
    let next = 1;
    while (next)
    {
        next = (first +
                second) % p;
        first = second;
        second = next;
        number++;
    }

    return number;
}

// Driver code
let p = 7;
document.write("Minimal zero is: ",
    findMinZero(p) + "<br>");

// This code is contributed
// by akt_mit
</script>

Output:

Minimal zero is: 8

This article is contributed by Aditi Sharma. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.