Fibonacci modulo p
Last Updated :
24 Mar, 2021
The Fibonacci sequence is defined as 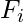 =
= 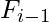 +
+ 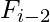 where
where 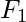 = 1 and
= 1 and 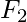 = 1 are the seeds.
= 1 are the seeds.
For a given prime number p, consider a new sequence which is (Fibonacci sequence) mod p. For example for p = 5, the new sequence would be 1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4 …
The minimal zero of the new sequence is defined as the first Fibonacci number that is a multiple of p or 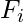 mod p = 0.
mod p = 0.
Given prime no p, find the minimal zero of the sequence Fibonacci modulo p.
Examples:
Input : 5
Output : 5
The fifth Fibonacci no (1 1 2 3 5)
is divisible by 5 so 5 % 5 = 0.
Input : 7
Output : 8
The 8th Fibonacci no (1 1 2 3 5 8 13 21)
is divisible by 7 so 21 % 7 = 0.
A simple approach is to keep calculating Fibonacci numbers and for each of them calculate Fi mod p. However if we observe this new sequence, let 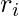 denote the
denote the 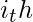 term of the sequence, then it follows :
term of the sequence, then it follows : 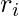 = (
= (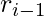 +
+ 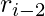 ) mod p. i.e. the remainder
) mod p. i.e. the remainder 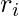 is actually the sum of remainders of previous two terms of this series. Therefore instead of generating the Fibonacci sequence and then taking modulo of each term we simply add previous two remainders and then take its modulo p.
is actually the sum of remainders of previous two terms of this series. Therefore instead of generating the Fibonacci sequence and then taking modulo of each term we simply add previous two remainders and then take its modulo p.
Below is the implementation to find the minimal 0.
C++
#include<bits/stdc++.h>
using namespace std;
int findMinZero(int p)
{
int first = 1, second = 1, number = 2, next = 1;
while (next)
{
next = (first + second) % p;
first = second;
second = next;
number++;
}
return number;
}
int main()
{
int p = 7;
cout << "Minimal zero is: "
<< findMinZero(p) << endl;
return 0;
}
|
Java
import java.io.*;
class FibZero
{
static int findMinZero(int p)
{
int first = 1, second = 1, number = 2, next = 1;
while (next > 0)
{
next = (first + second) % p;
first = second;
second = next;
number++;
}
return number;
}
public static void main (String[] args)
{
int p = 7;
System.out.println("Minimal zero is " + findMinZero(p));
}
}
|
Python3
def findMinZero(p):
first = 1
second = 1
number = 2
next = 1
while (next):
next = (first + second) % p
first = second
second = next
number = number + 1
return number
if __name__ == '__main__':
p = 7
print("Minimal zero is:", findMinZero(p))
|
C#
using System;
class GFG {
static int findMinZero(int p)
{
int first = 1, second = 1;
int number = 2, next = 1;
while (next > 0)
{
next = (first + second) % p;
first = second;
second = next;
number++;
}
return number;
}
public static void Main ()
{
int p = 7;
Console.WriteLine("Minimal zero "
+ "is :" + findMinZero(p));
}
}
|
PHP
<?php
function findMinZero($p)
{
$first = 1;
$second = 1;
$number = 2;
$next = 1;
while ($next)
{
$next = ($first +
$second) % $p;
$first = $second;
$second = $next;
$number++;
}
return $number;
}
$p = 7;
echo "Minimal zero is: ",
findMinZero($p), "\n";
?>
|
Javascript
<script>
function findMinZero(p)
{
let first = 1;
let second = 1;
let number = 2;
let next = 1;
while (next)
{
next = (first +
second) % p;
first = second;
second = next;
number++;
}
return number;
}
let p = 7;
document.write("Minimal zero is: ",
findMinZero(p) + "<br>");
</script>
|
Output:
Minimal zero is: 8
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...