Fast inverse square root
Last Updated :
30 Mar, 2023
Fast inverse square root is an algorithm that estimates 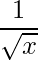 , the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number x in IEEE 754 floating-point format. Computing reciprocal square roots is necessary in many applications, such as vector normalization in video games and is mostly used in calculations involved in 3D programming. In 3D graphics, surface normals, 3-coordinate vectors of length 1 is used, to express lighting and reflection. There were a lot of surface normals. And calculating them involves normalizing a lot of vectors. Normalizing is often just a fancy term for division. The Pythagorean theorem computes distance between points, and dividing by distance helps normalize vectors:
, the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number x in IEEE 754 floating-point format. Computing reciprocal square roots is necessary in many applications, such as vector normalization in video games and is mostly used in calculations involved in 3D programming. In 3D graphics, surface normals, 3-coordinate vectors of length 1 is used, to express lighting and reflection. There were a lot of surface normals. And calculating them involves normalizing a lot of vectors. Normalizing is often just a fancy term for division. The Pythagorean theorem computes distance between points, and dividing by distance helps normalize vectors:
 This algorithm is best known for its implementation in 1999 in the source code of Quake III Arena Game, a first-person shooter video game that made heavy use of 3D graphics. At that time, it was generally computationally expensive to compute the reciprocal of a floating-point number, especially on a large scale; the fast inverse square root bypassed this step. Algorithm : Step 1 : It reinterprets the bits of the floating-point input as an integer.
This algorithm is best known for its implementation in 1999 in the source code of Quake III Arena Game, a first-person shooter video game that made heavy use of 3D graphics. At that time, it was generally computationally expensive to compute the reciprocal of a floating-point number, especially on a large scale; the fast inverse square root bypassed this step. Algorithm : Step 1 : It reinterprets the bits of the floating-point input as an integer.
i = * ( long * ) &y;
Step 2 : It takes the resulting value and does integer arithmetic on it which produces an approximation of the value we’re looking for.
i = 0x5f3759df - ( i >> 1 );
Step 3 : The result is not the approximation itself though, it is an integer which happens to be, if you reinterpret the bits as a floating point number, the approximation. So the code does the reverse of the conversion in step 1 to get back to floating point:
y = * ( float * ) &i;
Step 4 : And finally it runs a single iteration of Newton’s method to improve the approximation.
y = y * ( threehalfs - ( x2 * y * y ) ); //threehalfs = 1.5F;
The algorithm accepts a 32-bit floating-point number as the input and stores a halved value for later use. Then, treating the bits representing the floating-point number as a 32-bit integer, a logical shift right by one bit is performed and the result subtracted from the magic number 0x5F3759DF. This is the first approximation of the inverse square root of the input. Treating the bits again as a floating-point number, it runs one iteration of Newton’s approximation method, yielding a more precise approximation. Let’s say there is a number in exponent form or scientific notation: 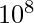 =100 million Now, to find the regular square root, we’d just divide the exponent by 2:
=100 million Now, to find the regular square root, we’d just divide the exponent by 2: 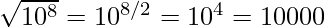 And if, want to know the inverse square root, divide the exponent by -2 to flip the sign:
And if, want to know the inverse square root, divide the exponent by -2 to flip the sign: 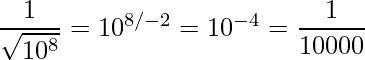 So, the code converts the floating-point number into an integer. It then shifts the bits by one, which means the exponent bits are divided by 2 (when we eventually turn the bits back into a float). And lastly, to negate the exponent, we subtract from the magic number 0x5f3759df. This does a few things: it preserves the mantissa (the non-exponent part, aka 5 in: 5 ·
So, the code converts the floating-point number into an integer. It then shifts the bits by one, which means the exponent bits are divided by 2 (when we eventually turn the bits back into a float). And lastly, to negate the exponent, we subtract from the magic number 0x5f3759df. This does a few things: it preserves the mantissa (the non-exponent part, aka 5 in: 5 · 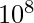 ), handles odd-even exponents, shifting bits from the exponent into the mantissa, and all sorts of funky stuff. The following code is the fast inverse square root implementation from Quake III Arena (exact original comment written in Quake III Arena Game).
), handles odd-even exponents, shifting bits from the exponent into the mantissa, and all sorts of funky stuff. The following code is the fast inverse square root implementation from Quake III Arena (exact original comment written in Quake III Arena Game).
CPP
#include<bits/stdc++.h>
using namespace std;
float inverse_rsqrt( float number )
{
const float threehalfs = 1.5F;
float x2 = number * 0.5F;
float y = number;
long i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) );
return y;
}
int main(){
int n = 256;
float f = inverse_rsqrt(n);
cout << f << endl;
return 0;
}
|
Java
public class FastInverseSqrt {
public static float inverse_rsqrt(float number) {
final float threehalfs = 1.5F;
float x2 = number * 0.5F;
float y = number;
int i = Float.floatToRawIntBits(y);
i = 0x5f3759df - (i >> 1);
y = Float.intBitsToFloat(i);
y = y * (threehalfs - (x2 * y * y));
return y;
}
public static void main(String[] args) {
int n = 256;
float f = inverse_rsqrt(n);
System.out.println(f);
}
}
|
Python3
import struct
def inverse_rsqrt(number):
threehalfs = 1.5
x2 = number * 0.5
y = number
i = struct.unpack('I', struct.pack('f', y))[0]
i = 0x5f3759df - (i >> 1)
y = struct.unpack('f', struct.pack('I', i))[0]
y = y * (threehalfs - (x2 * y * y))
result_bits = struct.unpack('I', struct.pack('f', y))[0]
size = struct.calcsize('I')
if result_bits < 0 or result_bits >= (1 << (size * 8)):
raise ValueError('result_bits out of range')
return struct.unpack('f', struct.pack('I', result_bits))[0]
if __name__ == '__main__':
n = 256
f = inverse_rsqrt(n)
print(f)
|
C#
using System;
class Gfg
{
static float inverse_rsqrt(float number)
{
const float threehalfs = 1.5F;
float x2 = number * 0.5F;
float y = number;
uint i = BitConverter.ToUInt32(BitConverter.GetBytes(y), 0);
i = 0x5f3759df - (i >> 1);
y = BitConverter.ToSingle(BitConverter.GetBytes(i), 0);
y = y * (threehalfs - (x2 * y * y));
return y;
}
static void Main(string[] args)
{
int n = 256;
float f = inverse_rsqrt(n);
Console.WriteLine(f);
}
}
|
Javascript
function inverse_rsqrt(number)
{
const threehalfs = 1.5;
let x2 = number * 0.5;
let y = number;
let i = new Int32Array(new Float32Array([y]).buffer)[0];
i = 0x5f3759df - (i >> 1);
y = new Float32Array(new Int32Array([i]).buffer)[0];
y = y * (threehalfs - (x2 * y * y));
return y;
}
let n = 256;
let f = inverse_rsqrt(n);
console.log(f);
|
Output :
0.0623942
Time Complexity: O(1)
Space Complexity: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...