A basic algebraic concept called factoring polynomials involves breaking down a polynomial equation into simpler parts. Factoring can be used to solve equations, simplify complicated expressions, and locate the roots or zeros of polynomial functions.
In several fields of mathematics, including engineering, physics, and computer science, the ability to factor is a crucial skill. Finding the common factors, or roots, of the equation and breaking them down into a set of simpler expressions are the general steps involved in factoring a polynomial.
What is Factoring of Polynomials?
The process by which we find the constituent factors of a higher-degree polynomial is called factoring polynomials.
For example, by multiplying x+2 and x -1 we get x2+x-2, where x + 2 and x -1 are the factors of the expression x2+x-2.
Thus, finding these factors from a given expression is called Factoring of Polynomial.
By the fundamental theorem of algebra, we know that any polynomial of degree n has n roots, either real or complex. Thus, it also has n factors as well. as every unique root gives a unique factor to the provided expression.
Steps for Factoring a Polynomial
For factorizing any polynomial, we need to follow three steps as follows:
- Firstly, factor out the common factor of all the terms of the given polynomial.
- Secondly, choose the best technique for factoring polynomials.
- And last, write all the factors as the product, as it gives the provided polynomial.
Techniques for Factoring Polynomials
Common Factors
The first method is the common factors method, in which if there is a common factor for each term in the polynomial, we factor that common term out and write the remaining polynomial.
The first approach is known as the “common factors method,” in which the common factors of each term are factored out in the polynomial.
Example: What are the factors of 3x2 + 6x +12?
Solution:
Let f(x) = 3x2 + 6x +12
As 3 is present in each term as expression can be rewritten as
f(x) =3x2+3×2x-3×4
⇒ f(x) = 3(x2+2x+4)
Thus, factors of the 3x2 + 6x +12 are 3 and x2 + 2x +4.
Grouping Method
This method factors polynomials by grouping terms with two or more terms together and finding the greatest common factor for each grouping. Once the common factors for each grouping were found, each group had the same factor.
Example: Factorize the expression ax2+7abx+ax+7ab as a and b are some real numbers.
Solution:
Let f(x) = ax2+7abx+ax+7ab
Grouping two elements at a time,
⇒ f(x) = (ax2+ax)+(7abx+7ab)
⇒ f(x) = ax(x+1)+7ab(x+1)
⇒ f(x) = (ax+7ab)(x+1)
Thus, ax+7ab and x + 1 are the required factors.
Splitting the Middle Term
Using this technique; the quadratic polynomials with a leading coefficient of 1, are factorized. This method is highly useful since higher-degree polynomials are frequently converted to quadratic polynomials using the factor theorem.
Step 1: f(x) = x2+(a+b)x+ab
Step 2: f(x)= x2+ax+bx+ab
Step 3: f(x)= x(x+a)+b(x+a)
Step 4: f(x)= (x+a)(x+b)
So all quadratic polynomial of form x2+(a+b)x+ab, can be factorize using Splitting the Middle Term method,
Example: Factorize x2+5x+6.
Solution:
Let f(x) = x2+5x+6
f(x)= x2 + (2+3)x+2×3
⇒ f(x)= x2+2x+3x+2×3
⇒ f(x)= x(x+2)+3(x+2)
⇒ f(x)= (x+2)(x+3)
Thus, x+2 and x+3 are the factors of the expression x2+5x+6.
Algebraic Identities
There are numerous Algebraic Identities that can be used to factorize different kinds and forms of polynomials. The following are some of the most commonly used identities:
- a2+b2+2ab = (a+b)2 = (a+b)(a+b)
- a2+b2-2ab = (a-b)2 = (a-b)(a-b)
- a2 – b2 = (a + b)(a – b)
- a2+b2+c2+2ab+2bc+2ca = (a+b+c)2 = (a+b+c)(a+b+c)
- a3 – b3 = (a – b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 – ab + b2)
- a4 – b4 = (a2 + b2)(a + b)(a – b)
Example: Factorize 16x4 – 9
Solution:
Let f(x) = 16x4 – 81
⇒ f(x) = (2x)4 – (3)4
⇒ f(x) = [(2x)2+32](2x+3)(2x-3)
⇒ f(x) = (4x2+9)(2x+3)(2x-3)
Thus, 4x2+9, 2x+3 and 2x-3 are the factors of expression 16x4 – 9.
Long Division Method
Long Division is a method for dividing polynomials similar to numbers, where a higher-degree polynomial can be divided by the lower-degree polynomial to find the quotient and remainder. Using long division and the factor and remainder theorem together, we can factorize any polynomial with an integer coefficient easily.
For example, Long division of x3-5x2+9x-5 by x -1 is shown in the following illustration.

Factor Theorem
Factor Theorem states that for any polynomial f(x) = 0, x – a is the factor of f(x) if and only if x = a is the zero of the polynomial.
Example: Use the Factor Theorem to determine whether x – 3 is a factor of f(x) = x3 – 6x2 + 11x – 6.
Solution:
By Factor Theorem we know, x – 3 is a factor of f(x) when f(3) = 0.
f(3) = 33 – 6(3)2 + 11(3) – 6
⇒ f(3)= 27 – 54 + 33 – 6 = 0
Since f(3) = 0, thus x – 3 is a factor of f(x).
Reminder Theorem
Remainder Theorem states that if x-a is the factor of a polynomial f(x)=0 then f(a) is the reminder of the polynomial when divided by x-a.
Example : Find the remainder when f(x) = 2x3 + 3x2 – 5x + 2 is divided by (x – 2).
Solution:
To find the remainder, we need to evaluate f(x) at x = 2, since the divisor is (x – 2).
Therefore, the remainder is:
f(2) = 2(2)3+ 3(2)2 – 5(2) + 2
f(2) = 16 + 12 – 10 + 2 = 20
Therefore, the remainder when f(x) is divided by (x – 2) is 20.
With the help of both the above-mentioned theorems and the long division method, most of the polynomials can be factorized. One of the examples is as follows
Example: f(x) = x3-6x2+3x+10
Solution:
Step 1: Consider all the divisors of the constant part of the polynomial and out of those divisors one should satisfy the given polynomial.
Constant part in the polynomial is 10 whose divisors are ±1, ±2, ±5.
Now, f(1) = 1 – 6 +3 +10 = 8 ≠ 0, So x – 1 is not a factor of f(x).
f(-1) = -1 – 6 -3 +10 = 0, thus x+1 is factor of f(x).
Step 2: Divide the polynomial f(x) with the newly found factor i.e., divide f(x) using long division by x+1.
So, f(x) = (x+1)(x2-7x+10)
Step 3: Factorize the remaining part using Splitting the Middle Term,
f(x) = (x+1)(x2-7x+10)
⇒ f(x) = (x+1)(x2-2x-5x+10)
⇒ f(x) = (x+1)[x(x-2)-5(x-2)]
⇒ f(x) = (x+1)(x-2)(x-5)
Thus, x+1, x-2 and x-5 are the factors of the polynomial f(x) = x3-6x2+3x+10
Sridharacharya Formula
For any quadratic equation ax2+bx+c =0, its two roots can be calculated using Sridharacharya Formula
and using factor theorem,  and
and  are the factors of the quadratic polynomial x2+(b/a)x+(c/a)
are the factors of the quadratic polynomial x2+(b/a)x+(c/a)
Related Resources
Solved Examples of Factoring Polynomial
Example 1: Factorize 7x2 – 21x.
Solution:
Let f(x) = 7x2 – 21x
As 7 and x is common in each term of the given polynomial
f(x) = 7x(x -3)
Hence, 7x and x – 3 are the factors of the given polynomial.
Example 2: What are the factors of y2-8y+7?
Solution:
Let g(y) = y2-8y+7
⇒ g(y) = y2-8y+7
⇒ g(y) = y2-7y-y+7
⇒ g(y) = y(y-7)-(y-7)
⇒ g(y) = (y-7)(y-1)
Thus, y-7 and y-1 are the factors of y2-8y+7.
Example 3: Factorize x2+x-1.
Solution:
Comparing x2+x-1 with the general quadratic expression ax2+bx+c, we get
a=1, b=1 and c=-1
Using Sridharacharya Formula,
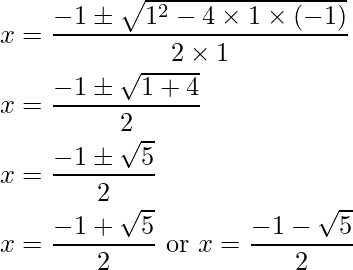
Thus, using factor theorem  and
and  are the factors of the given polynomial.
are the factors of the given polynomial.
Example 4: Factorize x3-5x2+9x-5.
Solution:
Let f(x) = x3-5x2+9x-5
As constant part is 5, and it’s divisors are ±1, ±5.
f(1) = 1 – 5 +9 -5 = 0
Thus, x-1 is factor of f(x).
Now, dividing f(x) using long division by x-1
Thus, f(x) = (x-1)(x2-4x+5)
As x2-4x+5 can’t be factored further,
So, x-1 and x2-4x+5 are the required factors of x3-5x2+9x-5.
FAQs on Factoring Polynomial
Question 1: What is factoring a polynomial?
Answer:
Factoring a polynomial is the process of expressing a higher-degree polynomial as the product of lower-degree polynomials. For example, the polynomial f(x) = 7x2 – 21x can be factorized as 7x(x-3), where 7, x, and x-3 are the factors of the given polynomial.
Question 2: What are the methods for factoring polynomials?
Answer:
There are a lot of methods for factoring polynomials, including factoring by grouping, factoring using the Sridharacharya Formula, factoring quadratic polynomials using the splitting the middle term method, using algebraic identities to factorize different polynomials, etc.
Question 3: What is the difference between a factor and a root of a polynomial?
Answer:
Factor is the lower-degree polynomial that can evenly divide the given polynomial and leave no remainder.
On the other hand, the root, or zero, of a polynomial is the real number for which the value of the polynomial becomes zero.
For example, for the polynomial f(x) = x2+ 2x+1 = (x + 1)2, (x + 1) is the factor of the polynomial, and x = -1 is the root of the polynomial.
Question 4: How can you check if a factor is correct?
Answer:
If the factors of the given polynomial are correct, then the product of all the factors is the polynomial itself. In other words, by multiplying all the factors of a polynomial together, we end up with the polynomial itself.
Question 5: How to Factorize Polynomials in 3 Degree?
Answer:
Follow the following steps to factorize a three-degree polynomial.
Step 1: For polynomial f(x) find its factor x – a such that f(a) = 0 by the hit and trial method.
Step 2: Using the long division method divide f(x) by x – a to get a two-degree polynomial.
Step 3: Factorize the two-degree polynomial obtained by the methods as discussed in the article.
Now, the three-degree polynomial f(x) is factorized.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...