Expected SARSA in Reinforcement Learning

Prerequisites: SARSA
SARSA and Q-Learning technique in Reinforcement Learning are algorithms that uses Temporal Difference(TD) Update to improve the agent’s behaviour. Expected SARSA technique is an alternative for improving the agent’s policy. It is very similar to SARSA and Q-Learning, and differs in the action value function it follows. 

Expected SARSA (State-Action-Reward-State-Action) is a reinforcement learning algorithm used for making decisions in an uncertain environment. It is a type of on-policy control method, meaning that it updates its policy while following it.

In Expected SARSA, the agent estimates the Q-value (expected reward) of each action in a given state, and uses these estimates to choose which action to take in the next state. The Q-value is defined as the expected cumulative reward that the agent will receive by taking a specific action in a specific state, and then following its policy from that state onwards.

The main difference between SARSA and Expected SARSA is in how they estimate the Q-value. SARSA estimates the Q-value using the Q-learning update rule, which selects the maximum Q-value of the next state and action pair. Expected SARSA, on the other hand, estimates the Q-value by taking a weighted average of the Q-values of all the possible actions in the next state. The weights are based on the probabilities of selecting each action in the next state, according to the current policy.

The steps of the Expected SARSA algorithm are as follows:

Initialize the Q-value estimates for each state-action pair to some initial value.

Repeat until convergence or a maximum number of iterations:
a. Observe the current state.
b. Choose an action according to the current policy, based on the estimated Q-values for that state.
c. Observe the reward and the next state.
d. Update the Q-value estimates for the current state-action pair, using the Expected SARSA update rule.
e. Update the policy for the current state, based on the estimated Q-values.

The Expected SARSA update rule is as follows:

Q(s, a) = Q(s, a) + α [R + γ ∑ π(a’|s’) Q(s’, a’) – Q(s, a)]

where:

Q(s, a) is the Q-value estimate for state s and action a.
α is the learning rate, which determines the weight given to new information.
R is the reward received for taking action a in state s and transitioning to the next state s’.
γ is the discount factor, which determines the importance of future rewards.
π(a’|s’) is the probability of selecting action a’ in state s’, according to the current policy.
Q(s’, a’) is the estimated Q-value for the next state-action pair.
Expected SARSA is a useful algorithm for reinforcement learning in scenarios where the agent must make decisions based on uncertain and changing environments. Its ability to estimate the expected reward of each action in the next state, taking into account the current policy, makes it a useful tool for online decision-making tasks.
We know that SARSA is an on-policy technique, Q-learning is an off-policy technique, but Expected SARSA can be use either as an on-policy or off-policy. This is where Expected SARSA is much more flexible compared to both these algorithms.
Let’s compare the action-value function of all the three algorithms and find out what is different in Expected SARSA. 

• SARSA:
• Q-Learning:
  
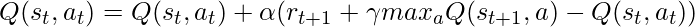
• Expected SARSA:
  

We see that Expected SARSA takes the weighted sum of all possible next actions with respect to the probability of taking that action. If the Expected Return is greedy with respect to the expected return, then this equation gets transformed to Q-Learning. Otherwise Expected SARSA is on-policy and computes the expected return for all actions, rather than randomly selecting an action like SARSA.
Keeping the theory and the formulae in mind, let us compare all the three algorithms, with an experiment. We shall implement a Cliff Walker as our environment provided by the gym library
Code: Python code to create the class Agent which will be inherited by the other agents to avoid duplicate code.

Python3

# Agent.py

import numpy as np

class Agent:
    """
    The Base class that is implemented by
    other classes to avoid the duplicate 'choose_action'
    method
    """
    def choose_action(self, state):
        action = 0
        if np.random.uniform(0, 1) < self.epsilon:
            action = self.action_space.sample()
        else:
            action = np.argmax(self.Q[state, :])
        return action

Code: Python code to create the SARSA Agent.

Python3

# SarsaAgent.py

import numpy as np
from Agent import Agent

class SarsaAgent(Agent):
    """
    The Agent that uses SARSA update to improve it's behaviour
    """
    def __init__(self, epsilon, alpha, gamma, num_state, num_actions, action_space):
        """
        Constructor
        Args:
            epsilon: The degree of exploration
            gamma: The discount factor
            num_state: The number of states
            num_actions: The number of actions
            action_space: To call the random action
        """
        self.epsilon = epsilon
        self.alpha = alpha
        self.gamma = gamma
        self.num_state = num_state
        self.num_actions = num_actions

        self.Q = np.zeros((self.num_state, self.num_actions))
        self.action_space = action_space

    def update(self, prev_state, next_state, reward, prev_action, next_action):
        """
        Update the action value function using the SARSA update.
        Q(S, A) = Q(S, A) + alpha(reward + (gamma * Q(S_, A_) - Q(S, A))
        Args:
            prev_state: The previous state
            next_state: The next state
            reward: The reward for taking the respective action
            prev_action: The previous action
            next_action: The next action
        Returns:
            None
        """
        predict = self.Q[prev_state, prev_action]
        target = reward + self.gamma * self.Q[next_state, next_action]
        self.Q[prev_state, prev_action] += self.alpha * (target - predict)

Code: Python code to create the Q-Learning Agent.

Python3

# QLearningAgent.py

import numpy as np
from Agent import Agent

class QLearningAgent(Agent):
    def __init__(self, epsilon, alpha, gamma, num_state, num_actions, action_space):
        """
        Constructor
        Args:
            epsilon: The degree of exploration
            gamma: The discount factor
            num_state: The number of states
            num_actions: The number of actions
            action_space: To call the random action
        """
        self.epsilon = epsilon
        self.alpha = alpha
        self.gamma = gamma
        self.num_state = num_state
        self.num_actions = num_actions

        self.Q = np.zeros((self.num_state, self.num_actions))
        self.action_space = action_space
    def update(self, state, state2, reward, action, action2):
        """
        Update the action value function using the Q-Learning update.
        Q(S, A) = Q(S, A) + alpha(reward + (gamma * Q(S_, A_) - Q(S, A))
        Args:
            prev_state: The previous state
            next_state: The next state
            reward: The reward for taking the respective action
            prev_action: The previous action
            next_action: The next action
        Returns:
            None
        """
        predict = self.Q[state, action]
        target = reward + self.gamma * np.max(self.Q[state2, :])
        self.Q[state, action] += self.alpha * (target - predict)

Code: Python code to create the Expected SARSA Agent. In this experiment we are using the following equation for the policy.

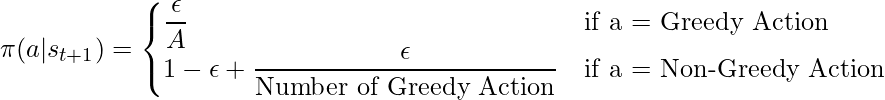
Python3

# ExpectedSarsaAgent.py

import numpy as np
from Agent import Agent

class ExpectedSarsaAgent(Agent):
    def __init__(self, epsilon, alpha, gamma, num_state, num_actions, action_space):
        """
        Constructor
        Args:
            epsilon: The degree of exploration
            gamma: The discount factor
            num_state: The number of states
            num_actions: The number of actions
            action_space: To call the random action
        """
        self.epsilon = epsilon
        self.alpha = alpha
        self.gamma = gamma
        self.num_state = num_state
        self.num_actions = num_actions

        self.Q = np.zeros((self.num_state, self.num_actions))
        self.action_space = action_space
    def update(self, prev_state, next_state, reward, prev_action, next_action):
        """
        Update the action value function using the Expected SARSA update.
        Q(S, A) = Q(S, A) + alpha(reward + (pi * Q(S_, A_) - Q(S, A))
        Args:
            prev_state: The previous state
            next_state: The next state
            reward: The reward for taking the respective action
            prev_action: The previous action
            next_action: The next action
        Returns:
            None
        """
        predict = self.Q[prev_state, prev_action]

        expected_q = 0
        q_max = np.max(self.Q[next_state, :])
        greedy_actions = 0
        for i in range(self.num_actions):
            if self.Q[next_state][i] == q_max:
                greedy_actions += 1

        non_greedy_action_probability = self.epsilon / self.num_actions
        greedy_action_probability = ((1 - self.epsilon) / greedy_actions) + non_greedy_action_probability

        for i in range(self.num_actions):
            if self.Q[next_state][i] == q_max:
                expected_q += self.Q[next_state][i] * greedy_action_probability
            else:
                expected_q += self.Q[next_state][i] * non_greedy_action_probability

        target = reward + self.gamma * expected_q
        self.Q[prev_state, prev_action] += self.alpha * (target - predict)

Python code to create an environment and Test all the three algorithms.

Python3

# main.py

import gym
import numpy as np

from ExpectedSarsaAgent import ExpectedSarsaAgent
from QLearningAgent import QLearningAgent
from SarsaAgent import SarsaAgent
from matplotlib import pyplot as plt

# Using the gym library to create the environment
env = gym.make('CliffWalking-v0')

# Defining all the required parameters
epsilon = 0.1
total_episodes = 500
max_steps = 100
alpha = 0.5
gamma = 1
"""
    The two parameters below is used to calculate
    the reward by each algorithm
"""
episodeReward = 0
totalReward = {
    'SarsaAgent': [],
    'QLearningAgent': [],
    'ExpectedSarsaAgent': []
}

# Defining all the three agents
expectedSarsaAgent = ExpectedSarsaAgent(
    epsilon, alpha, gamma, env.observation_space.n,
    env.action_space.n, env.action_space)
qLearningAgent = QLearningAgent(
    epsilon, alpha, gamma, env.observation_space.n,
    env.action_space.n, env.action_space)
sarsaAgent = SarsaAgent(
    epsilon, alpha, gamma, env.observation_space.n,
    env.action_space.n, env.action_space)

# Now we run all the episodes and calculate the reward obtained by
# each agent at the end of the episode

agents = [expectedSarsaAgent, qLearningAgent, sarsaAgent]

for agent in agents:
    for _ in range(total_episodes):
        # Initialize the necessary parameters before
        # the start of the episode
        t = 0
        state1 = env.reset()
        action1 = agent.choose_action(state1)
        episodeReward = 0
        while t < max_steps:

            # Getting the next state, reward, and other parameters
            state2, reward, done, info = env.step(action1)

            # Choosing the next action
            action2 = agent.choose_action(state2)

            # Learning the Q-value
            agent.update(state1, state2, reward, action1, action2)

            state1 = state2
            action1 = action2

            # Updating the respective vaLues
            t += 1
            episodeReward += reward

            # If at the end of learning process
            if done:
                break
        # Append the sum of reward at the end of the episode
        totalReward[type(agent).__name__].append(episodeReward)
env.close()

# Calculate the mean of sum of returns for each episode
meanReturn = {
    'SARSA-Agent': np.mean(totalReward['SarsaAgent']),
    'Q-Learning-Agent': np.mean(totalReward['QLearningAgent']),
    'Expected-SARSA-Agent': np.mean(totalReward['ExpectedSarsaAgent'])
}

# Print the results
print(f"SARSA Average Sum of Reward: {meanReturn['SARSA-Agent']}")
print(f"Q-Learning Average Sum of Return: {meanReturn['Q-Learning-Agent']}")
print(f"Expected Sarsa Average Sum of Return: {meanReturn['Expected-SARSA-Agent']}")

Output:

Conclusion: 
We have seen that Expected SARSA performs reasonably well in certain problems. It considers all possible outcomes before selecting a particular action. The fact that Expected SARSA can be used either as an off or on policy, is what makes this algorithm so dynamic.