exp() function C++
Last Updated :
08 Feb, 2023
The exp() function in C++ returns the exponential (Euler’s number) e (or 2.71828) raised to the given argument.
Syntax for returning exponential e: result=exp()
Parameter: The function can take any value i.e, positive, negative or zero in its parameter and returns result in int, double or float or long double. Return Value: The exp() function returns the value in the range of [0, inf].
Error:
- It shows error when we pass more than one argument in exp function
- When the input value is too large, the exp function can return inf or nan as a result, indicating overflow.
Application: Given below is an example of application of exp() function
CPP
#include <bits/stdc++.h>
using namespace std;
double application(double x)
{
double result = exp(x);
cout << "exp(x) = " << result << endl;
return result;
}
int main()
{
double x = 10;
cout << application(x);
return 0;
}
|
Outputexp(x) = 22026.5
22026.5
Time Complexity: O(1)
Auxiliary Space: O(1)
Here is the program to demonstrate the error in exp() function.
C++
#include <bits/stdc++.h>
using namespace std;
double application(double x)
{
double result = exp(x);
cout << "exp(x) = " << result << endl;
return result;
}
int main()
{
double x = 1000;
cout << application(x);
return 0;
}
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Applications of e (mathematical constant):
- Compound Interest : An account that starts at $1 and offers an annual interest rate of R will, after t years, yield eRt dollars with continuous compounding (Here R is the decimal equivalent of the rate of interest expressed as a percentage, so for 5% interest, R = 5/100 = 0.05)
- Value of below expression is e.
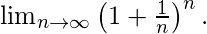
- The probability that a gambler never wins if he/she tries million times in a game where chances of winning in every trial is one by million is close to 1/e.
- The number e is the sum of the infinite series
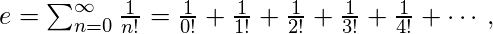
Source : Wiki
Share your thoughts in the comments
Please Login to comment...