Evaluation of Risk in Investments

Given two investment options A and B, we have to find the less risky investment of the two. The two investments A and B are each represented by an array. Each element in the array is a probable investment outcome. Thus each element in the array is a pair of two values. The first value is the amount of money received and the second value is the probability that this money can be received. For instance, if A = [ (100,0.1), (200,0.2) (300,0.7) ], it means that there is 10 % probability to earn Rs 100, 20% probability to earn Rs 200, and 70% chance to earn Rs 300 from investment A.

We have to use a statistical approach to solve the problem. For each investment, we first calculate the average amount of money that can be earned from it. Secondly, we also calculate the standard deviation in the money earned. Then we need to normalize this standard deviation by dividing it by the mean.

Each probable outcome is an observation. The probability for each amount of money is its frequency. Since the observations are given with frequencies we need to apply the following formulas to calculate the mean and standard deviation

If 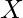$X$ denotes the set of observations $(x_i,f_i)$ .
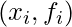Mean = 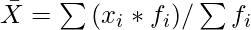$\bar X = \sum{(x_i * f_i)} / \sum{f_i}$
Standard deviation 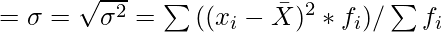$= \sigma = \sqrt{\sigma^2} = \sum{((x_i - \bar X)^2*f_i}) / \sum{f_i}$

Let us take an example to demonstrate how to apply this method.

Example:

Input:  A = [(0,0.1), (100,0.1), (200,0.2), (333,0.3), (400,0.3) ]
        B = [ (100,0.1), (200,0.5), (700,0.4) ]

Explanation:
Mean Investment of A
Index | Outcome | Probability | Probability*Outcome
(i)       (xi)        (fi)        xi*fi
----------------------------------------------------------
1          0          0.1            0
2        100          0.1           10
3        200          0.2           40
4        333          0.3         99.9
5        400          0.3          120
----------------------------------------------------------
Total:                1.0        269.1
Mean = 269.1/1 = 269.1

Mean Investment of B:
Index | Outcome | Probability | Probability*Outcome
(i)       (xi)        (fi)        xi*fi
----------------------------------------------------------
1        100          0.1           10
2        200          0.5          100
3        700          0.4          280
----------------------------------------------------------
Total:                1.0          390
Mean = 390/1 = 390.1

Standard Deviation of A
Mean = 269.1
Index | Outcome | Probability | (xi-Mean)^2 | A*fi
(i)       (xi)        (fi)        (A)
----------------------------------------------------------
1          0          0.1         72414.81  7241.481 
2        100          0.1         28594.81  2859.481
3        200          0.2          4774.81   954.962
4        333          0.3          4083.21  1224.963
5        400          0.3         17134.81  5140.443
----------------------------------------------------------
Total:                1.0                   17421.33
Standard Deviation  = sqrt(17421.33/1) = 131.989
Normalized Standard Deviation = 131.989/269.1 = 0.49

Standard Deviation of B
Mean = 390.1
Index | Outcome | Probability | (xi-Mean)^2 | A*fi
(i)       (xi)        (fi)        (A)
----------------------------------------------------------
1        100          0.1         84158.01   8415.801
2        200          0.5         36138.01  18069.005
3        700          0.4         96100.00  38440.000
----------------------------------------------------------
Total:                1.0                   64924.801
Standard Deviation  = sqrt(64924.801/1) = 254.803
Normalized Standard Deviation: 254.803 / 390.1 = 0.65

Since Investment A has lesser normalized standard deviation,
it is less risky.


Input: A = [(0,0.1), (100,0.1), (200,0.2), (333,0.3), (400,0.3) ]
       B = [ (100,0.1), (200,0.5), (700,0.4) ]

Explanation: 
For Investment A
Average: 269.9
Standard Deviation: 131.987
Normalised Std: 0.489024
For Investment B
Average: 258.333
Standard Deviation: 44.8764
Normalised Std: 0.173715
Investment B is less risky

The implementation of the problem is given below

C++

// C++ code for above approach
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
 
// First Item in the pair is the
// value of observation (xi).
// Second Item in the pair is
// the frequency of xi (fi)
typedef pair<float,float> Data;
 
// Vector stores the observation
// in pairs of format (xi, fi),
// where xi = value of observation
typedef vector<Data> Vector;
 
// Function to calculate the
// summation of fi*xi
float sigma_fx(const Vector & v)
{
    float sum = 0;
    for ( auto i : v) {
        sum += i.first * i.second;
    }
    return sum;
}
 
// Function to calculate summation fi
float sigma_f(const Vector & v)
{
    float sum = 0.0;
    for ( auto i : v) {
        sum += i.second;
    }
    return sum;
}
 
// Function to calculate the mean
// of the set of observations v
float calculate_mean(const Vector & v)
{
    return sigma_fx(v) / sigma_f(v);
}
 
// Function to calculate the std
// deviation of set of observations v
float calculate_std(const Vector & v)
{
    // Get sum of frequencies
    float f = sigma_f(v);
     
    // Get the mean of the set
    // of observations
    float mean = sigma_fx(v) / f;
     
    float sum = 0;
     
    for (auto i: v) {
        sum += (i.first-mean)*
               (i.first-mean)*i.second;
    }
     
    return sqrt(sum/f);
}
 
// Driver Code
int main()
{
     
    Vector A = { {0,0.1}, {100,0.1},
               {200,0.2}, {333,0.3}, {400,0.3}};
    Vector B = { {100,0.1}, {200,0.5}, {700,0.4}};
 
    float avg_A = calculate_mean(A);
    float avg_B = calculate_mean(B);
    float std_A = calculate_std(A);
    float std_B = calculate_std(B);
     
     
    cout << "For Investment A" << endl;
    cout << "Average: " << avg_A << endl;
    cout << "Standard Deviation: " <<
                           std_A << endl;
    cout << "Normalised Std: " <<
                    std_A / avg_A << endl;
    cout << "For Investment B" << endl;
    cout << "Average: " << avg_B << endl;
    cout << "Standard Deviation: " <<
                            std_B << endl;
    cout << "Normalised Std: " << std_B /
                            avg_B << endl;
     
    (std_B/avg_B) < (std_A/avg_A) ? cout <<
            "Investment B is less risky\n":
            cout << "Investment A is less risky\n";
     
    return 0;
}

Java

// Java code for above approach
import java.util.*;
import java.io.*;
 
public class GFG
{
    static class pair
    {
        float first, second;
 
        public pair(float first, float second)
        {
            this.first = first;
            this.second = second;
        }
    }
     
    // First Item in the pair is the
    // value of observation (xi).
    // Second Item in the pair is
    // the frequency of xi (fi)
 
    // Vector stores the observation
    // in pairs of format (xi, fi),
    // where xi = value of observation
    static Vector<pair> Vector;
 
    // Function to calculate the
    // summation of fi*xi
    static float sigma_fx(pair[] a)
    {
        float sum = 0;
        for (pair i : a)
        {
            sum += i.first * i.second;
        }
        return sum;
    }
 
    // Function to calculate summation fi
    static float sigma_f(pair[] a)
    {
        float sum = 0.0f;
        for (pair i : a)
        {
            sum += i.second;
        }
        return sum;
    }
 
    // Function to calculate the mean
    // of the set of observations v
    static float calculate_mean(pair[] a)
    {
        return sigma_fx(a) / sigma_f(a);
    }
 
    // Function to calculate the std
    // deviation of set of observations v
    static float calculate_std(pair[] a)
    {
         
        // Get sum of frequencies
        float f = sigma_f(a);
 
        // Get the mean of the set
        // of observations
        float mean = sigma_fx(a) / f;
 
        float sum = 0;
 
        for (pair i : a)
        {
            sum += (i.first - mean) *
                   (i.first - mean) * i.second;
        }
        return (float) Math.sqrt(sum / f);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        pair[] A = { new pair(0f, 0.1f),
                     new pair(100f, 0.1f),
                     new pair(200f, 0.2f),
                     new pair(333f, 0.3f),
                     new pair(400f, 0.3f) };
        pair[] B = { new pair(100f, 0.1f),
                     new pair(200f, 0.5f),
                     new pair(700f, 0.4f) };
 
        float avg_A = calculate_mean(A);
        float avg_B = calculate_mean(B);
        float std_A = calculate_std(A);
        float std_B = calculate_std(B);
 
        System.out.print("For Investment A" + "\n");
        System.out.print("Average: " + avg_A + "\n");
        System.out.print("Standard Deviation: " +
                                   std_A + "\n");
        System.out.print("Normalised Std: " +
                       std_A / avg_A + "\n");
        System.out.print("For Investment B" + "\n");
        System.out.print("Average: " + avg_B + "\n");
        System.out.print("Standard Deviation: " +
                                   std_B + "\n");
        System.out.print("Normalised Std: " +
                       std_B / avg_B + "\n");
 
        if ((std_B / avg_B) < (std_A / avg_A))
            System.out.print("Investment B is less risky\n");
        else
            System.out.print("Investment A is less risky\n");
    }
}
 
// This code is contributed by PrinciRaj1992

Python3

# Python3 code for above approach
 
# First Item in the pair is the
# value of observation (xi).
# Second Item in the pair is
# the frequency of xi (fi)
class Data:
 
    def __init__(self, x, y):
        self.first = x
        self.second = y
 
# Vector stores the observation
# in pairs of format (xi, fi),
# where xi = value of observations
Vector = []
 
# Function to calculate the
# summation of fi*xi
def sigma_fx(v):
 
    sum = 0
    for i in v:
        sum += i.first * i.second
 
    return sum
 
# Function to calculate summation fi
def sigma_f(v):
    sum = 0.0
    for i in v:
        sum += i.second
 
    return sum
 
# Function to calculate the mean
# of the set of observations v
def calculate_mean(v):
    return sigma_fx(v) / sigma_f(v)
 
# Function to calculate the std
# deviation of set of observations v
def calculate_std(v):
 
    # Get sum of frequencies
    f = sigma_f(v)
 
    # Get the mean of the set
    # of observations
    mean = sigma_fx(v) / f
 
    sum = 0
 
    for i in v:
        sum += (i.first-mean) * (i.first-mean)*i.second
 
    return (sum/f) ** 0.5
 
 
# Driver Code
A = [Data(0, 0.1), Data(100, 0.1), Data(
    200, 0.2), Data(333, 0.3), Data(400, 0.3)]
B = [Data(100, 0.1), Data(200, 0.5), Data(700, 0.4)]
 
avg_A = calculate_mean(A)
avg_B = calculate_mean(B)
std_A = calculate_std(A)
std_B = calculate_std(B)
 
 
print("For Investment A")
print("Average:", avg_A)
print("Standard Deviation:",  std_A)
print("Normalised Std:", std_A / avg_A)
print("For Investment B")
print("Average:", avg_B)
print("Standard Deviation:", std_B)
print("Normalised Std:", std_B / avg_B)
 
if (std_B/avg_B) < (std_A/avg_A):
    print("Investment B is less risky")
else:
    print("Investment A is less risky")
 
# This code is contributed by phasing17

C#

// C# code for above approach
using System;
using System.Collections.Generic;
 
class GFG
{
    class pair
    {
        public float first, second;
 
        public pair(float first,
                    float second)
        {
            this.first = first;
            this.second = second;
        }
    }
     
    // First Item in the pair is the
    // value of observation (xi).
    // Second Item in the pair is
    // the frequency of xi (fi)
 
    // List stores the observation
    // in pairs of format (xi, fi),
    // where xi = value of observation
    static List<pair> List;
 
    // Function to calculate the
    // summation of fi*xi
    static float sigma_fx(pair[] a)
    {
        float sum = 0;
        foreach (pair i in a)
        {
            sum += i.first * i.second;
        }
        return sum;
    }
 
    // Function to calculate summation fi
    static float sigma_f(pair[] a)
    {
        float sum = 0.0f;
        foreach (pair i in a)
        {
            sum += i.second;
        }
        return sum;
    }
 
    // Function to calculate the mean
    // of the set of observations v
    static float calculate_mean(pair[] a)
    {
        return sigma_fx(a) / sigma_f(a);
    }
 
    // Function to calculate the std
    // deviation of set of observations v
    static float calculate_std(pair[] a)
    {
         
        // Get sum of frequencies
        float f = sigma_f(a);
 
        // Get the mean of the set
        // of observations
        float mean = sigma_fx(a) / f;
 
        float sum = 0;
 
        foreach (pair i in a)
        {
            sum += (i.first - mean) *
                   (i.first - mean) * i.second;
        }
        return (float) Math.Sqrt(sum / f);
    }
 
    // Driver Code
    public static void Main(String[] args)
    {
        pair[] A = {new pair(0f, 0.1f),
                    new pair(100f, 0.1f),
                    new pair(200f, 0.2f),
                    new pair(333f, 0.3f),
                    new pair(400f, 0.3f)};
        pair[] B = {new pair(100f, 0.1f),
                    new pair(200f, 0.5f),
                    new pair(700f, 0.4f)};
 
        float avg_A = calculate_mean(A);
        float avg_B = calculate_mean(B);
        float std_A = calculate_std(A);
        float std_B = calculate_std(B);
 
        Console.Write("For Investment A" + "\n");
        Console.Write("Average: " + avg_A + "\n");
        Console.Write("Standard Deviation: " +
                                std_A + "\n");
        Console.Write("Normalised Std: " +
                    std_A / avg_A + "\n");
        Console.Write("For Investment B" + "\n");
        Console.Write("Average: " + avg_B + "\n");
        Console.Write("Standard Deviation: " +
                                std_B + "\n");
        Console.Write("Normalised Std: " +
                    std_B / avg_B + "\n");
 
        if ((std_B / avg_B) < (std_A / avg_A))
            Console.Write("Investment B is less risky\n");
        else
            Console.Write("Investment A is less risky\n");
    }
}
 
// This code is contributed by Rajput-Ji

Javascript

// JavaScript code for above approach
 
 
// First Item in the pair is the
// value of observation (xi).
// Second Item in the pair is
// the frequency of xi (fi)
class Data
{
    constructor(x, y)
    {
        this.first = x;
        this.second = y;
    }
}
 
// Vector stores the observation
// in pairs of format (xi, fi),
// where xi = value of observations
let Vector = new Array();
 
// Function to calculate the
// summation of fi*xi
function sigma_fx(v)
{
    let sum = 0;
    for (var i of v) {
        sum += i.first * i.second;
    }
    return sum;
}
 
// Function to calculate summation fi
function sigma_f(v)
{
    let sum = 0.0;
    for (let i of v) {
        sum += i.second;
    }
    return sum;
}
 
// Function to calculate the mean
// of the set of observations v
function calculate_mean(v)
{
    return sigma_fx(v) / sigma_f(v);
}
 
// Function to calculate the std
// deviation of set of observations v
function calculate_std(v)
{
    // Get sum of frequencies
    let f = sigma_f(v);
     
    // Get the mean of the set
    // of observations
    let mean = sigma_fx(v) / f;
     
    let sum = 0;
     
    for (var i of v) {
        sum += (i.first-mean)*
               (i.first-mean)*i.second;
    }
     
    return Math.sqrt(sum/f);
}
 
// Driver Code
let A = [new Data(0,0.1), new Data(100,0.1),
               new Data(200,0.2), new Data(333,0.3), new Data(400,0.3)];
let B = [ new Data(100,0.1), new Data(200,0.5), new Data(700,0.4)];
 
let avg_A = calculate_mean(A);
let avg_B = calculate_mean(B);
let std_A = calculate_std(A);
let std_B = calculate_std(B);
     
     
console.log("For Investment A");
console.log("Average: " + avg_A);
console.log("Standard Deviation: " +  std_A);
console.log("Normalised Std: " + std_A / avg_A);
console.log("For Investment B");
console.log("Average: " + avg_B);
console.log("Standard Deviation: " + std_B);
console.log("Normalised Std: " + std_B / avg_B);
     
((std_B/avg_B) < (std_A/avg_A)) ? console.log("Investment B is less risky"):
            console.log("Investment A is less risky");
 
 
// This code is contributed by phasing17

Output

For Investment A
Average: 269.9
Standard Deviation: 131.987
Normalised Std: 0.489024
For Investment B
Average: 390
Standard Deviation: 254.755
Normalised Std: 0.653217
Investment A is less risky

Time complexity: O(n)
Auxiliary Space: O(1)

References:
https://www.statcan.gc.ca/edu/power-pouvoir/ch12/5214891-eng.htm
std::accumulate cppreference.com

Recommended

Solve DSA problems on GfG Practice.

Solve Problems

Last Updated : 21 Dec, 2022