Evaluate 2 sin 30° – 3 cos 45° + tan 60°

Trigonometry is the branch of mathematics that deals with triangles and angles associated with it. if we break the word into 2 parts namely trigon and geometry, we can understand easily that this branch of mathematics deals with the geometry of triangles. Using trigonometry, the properties of triangles and their applications can be easily understood. Using trigonometry, one can find the angles and missing sides of any triangle with the use of trigonometric ratios.

Trigonometric Ratios

There are six functions or trigonometric ratios of an angle that are present in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). One important thing to note here is that trigonometric formulas work only on the right-angle triangle. Let’s see the below image.

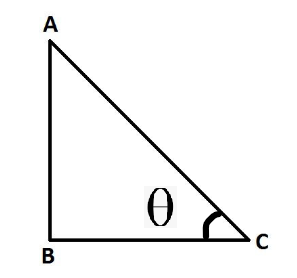
In this right-angle triangle, side AC is known as hypotenuse. side BC is known as the base of the triangle. side AB is known as the height of the triangle. From the above triangle, we can list out formulas as above,

• sin∅ = AB/AC
• cos∅ = BC/AC
• tan∅ = AB/BC
• cot∅ = BC/AB
• cosec∅ = AC/AB
• sec∅ = AC/BC
• sin(90° – x) = cos x
• cos(90° – x) = sin x
• tan(90° – x) = cot x
• cot(90° – x) = tan x

Trigonometric Angles Table

Below is the table which shows the basic values of trigonometric functions against common angles vis 0°, 30°, 45°, 60°, 90°. the below table must be by heart in order to solve trigonometric-related problems.

Ratio\Angle	0°	30°	45°	60°	90°
sin(θ)	0	1/2	1/√2	√3/2	1
cos(θ)	1	√3/2	1/√2	1/2	0
tan(θ)	0	1/√3	1	√3	∞
cosec(θ)	∞	2	√2	2/√3	1
sec(θ)	1	2/√3	√2	2	∞
cot(θ)	∞	√3	1	1/√3	0

Evaluate 2 sin 30° – 3 cos 45° + tan 60°

Solution:

From the above table, we know that sin 30° = 1/2, cos45° = 1/2, tan60° = √3

Substituting the above values,

2 × 1/2 – 3/√2 + √3 

=1 – 2.12 + √3 = 0.612

Similar Problems

Question 1: Evaluate tan45° + cot45°

Solution:

From the above table, we know that tan45° = cot45° = 1

Substituting the above values,

1 + 1 = 2

Question 2: Evaluate √3sec30° – √2cosec45°

Solution:

From the above table, we know that sec30° = 2/√3 and cosec45° = √2

Substituting the above values,

√3 × 2/√3 – √2 × √2

2 – 2 = 0

Question 3: Evaluate 2sin60° + 5tan0°

Solution:

From the above table, we know that sin60° = √3/2 and tan0° = 0

Substituting the above values,

2 × √3/2 + 5 × 0

√3 = 0.71

Question 4: Evaluate 4cot60° + 2sin90° – cos0°

Solution:

From the above table, we know that cot60° = 1/√3, sin 90° = 1, cos0° = 1

Substituting the above values,

4 × 1/√3 + 2 × 1-1

= 1.309