Eulerian path and circuit for undirected graph
Last Updated :
06 Feb, 2023
Eulerian Path is a path in a graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path that starts and ends on the same vertex.
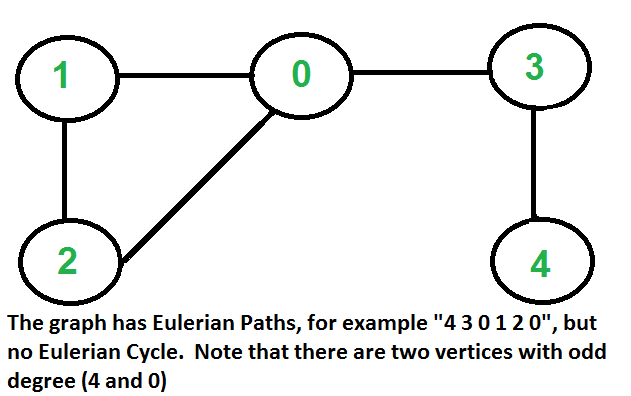
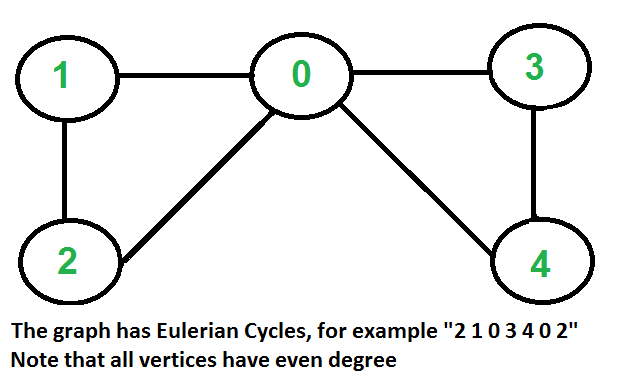
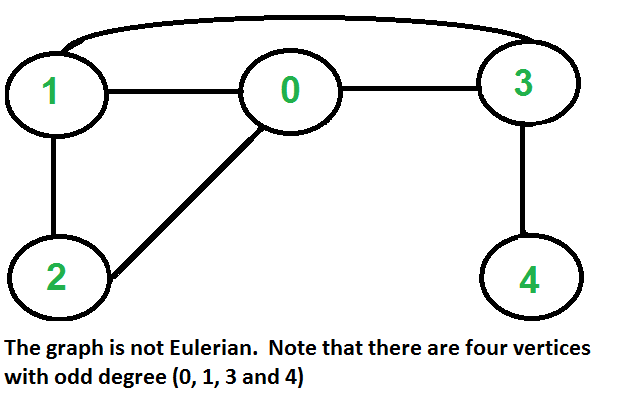
How to find whether a given graph is Eulerian or not?
The problem is same as following question. “Is it possible to draw a given graph without lifting pencil from the paper and without tracing any of the edges more than once”.
A graph is called Eulerian if it has an Eulerian Cycle and called Semi-Eulerian if it has an Eulerian Path. The problem seems similar to Hamiltonian Path which is NP complete problem for a general graph. Fortunately, we can find whether a given graph has a Eulerian Path or not in polynomial time. In fact, we can find it in O(V+E) time.
Following are some interesting properties of undirected graphs with an Eulerian path and cycle. We can use these properties to find whether a graph is Eulerian or not.
Eulerian Cycle: An undirected graph has Eulerian cycle if following two conditions are true.
- All vertices with non-zero degree are connected. We don’t care about vertices with zero degree because they don’t belong to Eulerian Cycle or Path (we only consider all edges).
- All vertices have even degree.
Eulerian Path: An undirected graph has Eulerian Path if following two conditions are true.
- Same as condition (a) for Eulerian Cycle.
- If zero or two vertices have odd degree and all other vertices have even degree. Note that only one vertex with odd degree is not possible in an undirected graph (sum of all degrees is always even in an undirected graph)
Note that a graph with no edges is considered Eulerian because there are no edges to traverse.
How does this work?
In Eulerian path, each time we visit a vertex v, we walk through two unvisited edges with one end point as v. Therefore, all middle vertices in Eulerian Path must have even degree. For Eulerian Cycle, any vertex can be middle vertex, therefore all vertices must have even degree.
Implementation:
C++
#include<iostream>
#include <list>
using namespace std;
class Graph
{
int V;
list<int> *adj;
public:
Graph(int V) {this->V = V; adj = new list<int>[V]; }
~Graph() { delete [] adj; }
void addEdge(int v, int w);
int isEulerian();
bool isConnected();
void DFSUtil(int v, bool visited[]);
};
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
void Graph::DFSUtil(int v, bool visited[])
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i, visited);
}
bool Graph::isConnected()
{
bool visited[V];
int i;
for (i = 0; i < V; i++)
visited[i] = false;
for (i = 0; i < V; i++)
if (adj[i].size() != 0)
break;
if (i == V)
return true;
DFSUtil(i, visited);
for (i = 0; i < V; i++)
if (visited[i] == false && adj[i].size() > 0)
return false;
return true;
}
int Graph::isEulerian()
{
if (isConnected() == false)
return 0;
int odd = 0;
for (int i = 0; i < V; i++)
if (adj[i].size() & 1)
odd++;
if (odd > 2)
return 0;
return (odd)? 1 : 2;
}
void test(Graph &g)
{
int res = g.isEulerian();
if (res == 0)
cout << "graph is not Eulerian\n";
else if (res == 1)
cout << "graph has a Euler path\n";
else
cout << "graph has a Euler cycle\n";
}
int main()
{
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
test(g1);
Graph g2(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.addEdge(4, 0);
test(g2);
Graph g3(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(1, 3);
test(g3);
Graph g4(3);
g4.addEdge(0, 1);
g4.addEdge(1, 2);
g4.addEdge(2, 0);
test(g4);
Graph g5(3);
test(g5);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
import java.util.LinkedList;
class Graph
{
private int V;
private LinkedList<Integer> adj[];
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
void addEdge(int v, int w)
{
adj[v].add(w);
adj[w].add(v);
}
void DFSUtil(int v,boolean visited[])
{
visited[v] = true;
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
boolean isConnected()
{
boolean visited[] = new boolean[V];
int i;
for (i = 0; i < V; i++)
visited[i] = false;
for (i = 0; i < V; i++)
if (adj[i].size() != 0)
break;
if (i == V)
return true;
DFSUtil(i, visited);
for (i = 0; i < V; i++)
if (visited[i] == false && adj[i].size() > 0)
return false;
return true;
}
int isEulerian()
{
if (isConnected() == false)
return 0;
int odd = 0;
for (int i = 0; i < V; i++)
if (adj[i].size()%2!=0)
odd++;
if (odd > 2)
return 0;
return (odd==2)? 1 : 2;
}
void test()
{
int res = isEulerian();
if (res == 0)
System.out.println("graph is not Eulerian");
else if (res == 1)
System.out.println("graph has a Euler path");
else
System.out.println("graph has a Euler cycle");
}
public static void main(String args[])
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.test();
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.addEdge(4, 0);
g2.test();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(1, 3);
g3.test();
Graph g4 = new Graph(3);
g4.addEdge(0, 1);
g4.addEdge(1, 2);
g4.addEdge(2, 0);
g4.test();
Graph g5 = new Graph(3);
g5.test();
}
}
|
Python3
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = defaultdict(list)
def addEdge(self, u, v):
self.graph[u].append(v)
self.graph[v].append(u)
def DFSUtil(self, v, visited):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.DFSUtil(i, visited)
def isConnected(self):
visited = [False]*(self.V)
for i in range(self.V):
if len(self.graph[i]) != 0:
break
if i == self.V-1:
return True
self.DFSUtil(i, visited)
for i in range(self.V):
if visited[i] == False and len(self.graph[i]) > 0:
return False
return True
def isEulerian(self):
if self.isConnected() == False:
return 0
else:
odd = 0
for i in range(self.V):
if len(self.graph[i]) % 2 != 0:
odd += 1
if odd == 0:
return 2
elif odd == 2:
return 1
elif odd > 2:
return 0
def test(self):
res = self.isEulerian()
if res == 0:
print("graph is not Eulerian")
elif res == 1:
print("graph has a Euler path")
else:
print("graph has a Euler cycle")
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
g1.test()
g2 = Graph(5)
g2.addEdge(1, 0)
g2.addEdge(0, 2)
g2.addEdge(2, 1)
g2.addEdge(0, 3)
g2.addEdge(3, 4)
g2.addEdge(4, 0)
g2.test()
g3 = Graph(5)
g3.addEdge(1, 0)
g3.addEdge(0, 2)
g3.addEdge(2, 1)
g3.addEdge(0, 3)
g3.addEdge(3, 4)
g3.addEdge(1, 3)
g3.test()
g4 = Graph(3)
g4.addEdge(0, 1)
g4.addEdge(1, 2)
g4.addEdge(2, 0)
g4.test()
g5 = Graph(3)
g5.test()
|
C#
using System;
using System.Collections.Generic;
public class Graph
{
private int V;
private List<int> []adj;
Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i=0; i<v; ++i)
adj[i] = new List<int>();
}
void addEdge(int v, int w)
{
adj[v].Add(w);
adj[w].Add(v);
}
void DFSUtil(int v,bool []visited)
{
visited[v] = true;
foreach(int i in adj[v]){
int n = i;
if (!visited[n])
DFSUtil(n, visited);
}
}
bool isConnected()
{
bool []visited = new bool[V];
int i;
for (i = 0; i < V; i++)
visited[i] = false;
for (i = 0; i < V; i++)
if (adj[i].Count != 0)
break;
if (i == V)
return true;
DFSUtil(i, visited);
for (i = 0; i < V; i++)
if (visited[i] == false && adj[i].Count > 0)
return false;
return true;
}
int isEulerian()
{
if (isConnected() == false)
return 0;
int odd = 0;
for (int i = 0; i < V; i++)
if (adj[i].Count%2!=0)
odd++;
if (odd > 2)
return 0;
return (odd==2)? 1 : 2;
}
void test()
{
int res = isEulerian();
if (res == 0)
Console.WriteLine("graph is not Eulerian");
else if (res == 1)
Console.WriteLine("graph has a Euler path");
else
Console.WriteLine("graph has a Euler cycle");
}
public static void Main(String []args)
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.test();
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.addEdge(4, 0);
g2.test();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(1, 3);
g3.test();
Graph g4 = new Graph(3);
g4.addEdge(0, 1);
g4.addEdge(1, 2);
g4.addEdge(2, 0);
g4.test();
Graph g5 = new Graph(3);
g5.test();
}
}
|
Javascript
<script>
class Graph
{
constructor(v)
{
this.V = v;
this.adj = new Array(v);
for (let i = 0; i < v; ++i)
this.adj[i] = [];
}
addEdge(v,w)
{
this.adj[v].push(w);
this.adj[w].push(v);
}
DFSUtil(v,visited)
{
visited[v] = true;
for(let i of this.adj[v])
{
let n = i;
if (!visited[n])
this.DFSUtil(n, visited);
}
}
isConnected()
{
let visited = new Array(this.V);
let i;
for (i = 0; i < this.V; i++)
visited[i] = false;
for (i = 0; i < this.V; i++)
if (this.adj[i].length != 0)
break;
if (i == this.V)
return true;
this.DFSUtil(i, visited);
for (i = 0; i < this.V; i++)
if (visited[i] == false && this.adj[i].length > 0)
return false;
return true;
}
isEulerian()
{
if (this.isConnected() == false)
return 0;
let odd = 0;
for (let i = 0; i < this.V; i++)
if (this.adj[i].length%2!=0)
odd++;
if (odd > 2)
return 0;
return (odd==2)? 1 : 2;
}
test()
{
let res = this.isEulerian();
if (res == 0)
document.write("graph is not Eulerian<br>");
else if (res == 1)
document.write("graph has a Euler path<br>");
else
document.write("graph has a Euler cycle<br>");
}
}
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.test();
let g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.addEdge(4, 0);
g2.test();
let g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(1, 3);
g3.test();
let g4 = new Graph(3);
g4.addEdge(0, 1);
g4.addEdge(1, 2);
g4.addEdge(2, 0);
g4.test();
let g5 = new Graph(3);
g5.test();
</script>
|
Output
graph has a Euler path
graph has a Euler cycle
graph is not Eulerian
graph has a Euler cycle
graph has a Euler cycle
Time Complexity: O(V+E)
Space Complexity: O(V+E)
Next Articles:
Eulerian Path and Circuit for a Directed Graphs.
Fleury’s Algorithm to print a Eulerian Path or Circuit?
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...