Euler zigzag numbers ( Alternating Permutation )
Last Updated :
28 May, 2022
Euler Zigzag numbers is a sequence of integers which is a number of arrangements of those numbers so that each entry is alternately greater or less than the preceding entry.
c1, c2, c3, c4 is Alternating permutation where
c1 < c2
c3 < c2
c3 < c4…
zigzag numbers are as follows 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521 ……
For a given integer N. The task is to print sequence up to N terms.
Examples:
Input : N = 10
Output : 1 1 1 2 5 16 61 272 1385 7936
Input : N = 14
Output : 1 1 1 2 5 16 61 272 1385 7936 50521 353792 2702765 22368256
Approach :
The (n+1)th Zigzag number is :
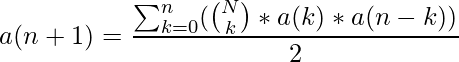
We will find the factorial upto n and store them in an array and also create a second array to store the i th zigzag number and apply the formula stated above to find all the n zigzag numbers.
Below is the implementation of the above approach :
C++
#include <bits/stdc++.h>
using namespace std;
void ZigZag(int n)
{
long long fact[n + 1], zig[n + 1] = { 0 };
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = fact[i - 1] * i;
zig[0] = 1;
zig[1] = 1;
cout << "zig zag numbers: ";
cout << zig[0] << " " << zig[1] << " ";
for (int i = 2; i < n; i++)
{
long long sum = 0;
for (int k = 0; k <= i - 1; k++)
{
sum += (fact[i - 1]/(fact[i - 1 - k]*fact[k]))
*zig[k] * zig[i - 1 - k];
}
zig[i] = sum / 2;
cout << sum / 2 << " ";
}
}
int main()
{
int n = 10;
ZigZag(n);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG
{
static void ZigZag(int n)
{
long[] fact= new long[n + 1];
long[] zig = new long[n + 1];
for (int i = 0; i < n + 1; i++)
zig[i] = 0;
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = fact[i - 1] * i;
zig[0] = 1;
zig[1] = 1;
System.out.print("zig zag numbers: ");
System.out.print(zig[0] + " " + zig[1] + " ");
for (int i = 2; i < n; i++)
{
long sum = 0;
for (int k = 0; k <= i - 1; k++)
{
sum += (fact[i - 1] / (fact[i - 1 - k] *
fact[k])) * zig[k] * zig[i - 1 - k];
}
zig[i] = sum / 2;
System.out.print(sum / 2 + " " );
}
}
public static void main (String[] args)
throws java.lang.Exception
{
int n = 10;
ZigZag(n);
}
}
|
Python3
def ZigZag(n):
fact = [0 for i in range(n + 1)]
zig = [0 for i in range(n + 1)]
fact[0] = 1
for i in range(1, n + 1):
fact[i] = fact[i - 1] * i
zig[0] = 1
zig[1] = 1
print("zig zag numbers: ", end = " ")
print(zig[0], zig[1], end = " ")
for i in range(2, n):
sum = 0
for k in range(0, i):
sum += ((fact[i - 1] //
(fact[i - 1 - k] * fact[k])) *
zig[k] * zig[i - 1 - k])
zig[i] = sum // 2
print(sum // 2, end = " ")
n = 10
ZigZag(n)
|
C#
using System;
class GFG
{
static void ZigZag(int n)
{
long[] fact= new long[n + 1];
long[] zig = new long[n + 1];
for (int i = 0; i < n + 1; i++)
zig[i] = 0;
fact[0] = 1;
for (int i = 1; i <= n; i++)
fact[i] = fact[i - 1] * i;
zig[0] = 1;
zig[1] = 1;
Console.Write("zig zag numbers: ");
Console.Write(zig[0] + " " + zig[1] + " ");
for (int i = 2; i < n; i++)
{
long sum = 0;
for (int k = 0; k <= i - 1; k++)
{
sum += (fact[i - 1] / (fact[i - 1 - k] *
fact[k])) * zig[k] * zig[i - 1 - k];
}
zig[i] = sum / 2;
Console.Write(sum / 2 + " " );
}
}
public static void Main (String[] args)
{
int n = 10;
ZigZag(n);
}
}
|
Javascript
<script>
function ZigZag(n)
{
var fact = Array(n+1).fill(0);
var zig = Array(n+1).fill(0);
fact[0] = 1;
for (var i = 1; i <= n; i++)
fact[i] = fact[i - 1] * i;
zig[0] = 1;
zig[1] = 1;
document.write( "zig zag numbers: ");
document.write( zig[0] + " " + zig[1] + " ");
for (var i = 2; i < n; i++)
{
var sum = 0;
for (var k = 0; k <= i - 1; k++)
{
sum += parseInt(fact[i - 1]/(fact[i - 1 - k]*fact[k]))
*zig[k] * zig[i - 1 - k];
}
zig[i] = parseInt(sum / 2);
document.write( parseInt(sum / 2) + " ");
}
}
var n = 10;
ZigZag(n);
</script>
|
Output:
zig zag numbers: 1 1 1 2 5 16 61 272 1385 7936
Time Complexity: O(n2)
Auxiliary Space: O(n)
Reference
https://en.wikipedia.org/wiki/Alternating_permutation
https://oeis.org/A000111
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...